J o a c h i m M o h r Mathematik Musik Programmieren

Die gute Intonation

Hier erfahren Sie, dass die Stimmung des Klaviers ein Kompromiss in der Intonation ist. Dies hängt mit der großen Terz zusammen. Ein kleines Intervall, das pythagoreische - und noch wichtiger - das syntonische Komma spielt hier ein große Rolle: Die pythagoreische - dissonante - große Terz ist nämlich ein Komma größer als die reine - wohlklingende - große Terz.

Die pythagoreische Terz im Vergleich zur reinen Terz

Hinweis: Hier ist bei Intervallangaben x-y der zweite Ton y immer höher als der erste x. Zum Beispiel sind die Intervalle c-g und g-d Quinten und c-c eine Oktave.

In der zweiten Hälfte des 15. Jahrhunderts entdeckte man mit dem Aufkommen der Mehrstimmigkeit die reine große Terz (mit dem Frequenzverhältnis ⁵/₄), die im bisherigen pythagoreischen Tonsystem beim einstimmigen Musizieren keine Rolle spielte.
Dadurch veränderte sich die diatonische Tonleiter, c-d-e-f-g-a-h-c, die bisher aus 5 Ganztönen c-d, d-e, f-g, g-a und a-h sowie aus zwei Halbtönen f-e und h-c bestand. Eingestimmt wurde diese Tonleiter durch die reinen Quinten (mit dem Frequenzverhältnis ³/₂) f-c, c-g, g-d, d-a, a-e und e-h.

Beim A-Capella-Gesang erklang ein Dreiklang mit großer Terz besser als auf einer Orgel. Das hängt mit den Obertönen zusammen. Ein Oberton jedes Grundtones ist neben der Oktave und Quinte die Terz, als reine Terz bezeichnet, die oktaviert das Frequenzverhältnis ⁵/₄ mit dem Grundton bildet. Die Terz auf den damals eingestimmten Instrumenten ist eine pythagoreische Terz mit dem Frequenzverhältnis ⁸¹/₆₄ und wurde wegen der heftigen Schwebungen in den Obertönen damals als dissonant empfunden.

Die reine Stimmung

Ab der Mitte des 16. Jahrhunderts werden in Musikschulen sehr anschaulich die Größenverhältnissen von Intervallen beschrieben. Das kleinste Intervall ist das Mercator-Komma k, fast gleich groß wie das syntonische Komma (Zur Genauigkeit: siehe hier...).

In dieser Schreibweise ist die diatonische Tonleiter in pythagoreischer (siehe unten) und reiner Stimmung:
(Die folgende Schreibweise mit dem Tiefkomma vor der Tonbezeichnung ,e bedeutet, dass das e der pythagoreischen Tonleiter um ein k erniedrigt wird.)

Dass in der reinen Stimmung die
Ganztöne mal 8k, mal 9k groß sind,
spielt bei Melodien keine Rolle.
Aber wohl in der Harmonie der Klänge.
Die Akkorde c-,e-g und f-,a-c
sowie g-,h-d erzwangen, dass in der
Theorie mit c-d=9k und d-,e=8k usw.
gerechnet werden musste.
In Klammer werden die zugehörigen
Frequenzverhältnisse angegeben.
4k=pythagoreisches Leimma,
5k=diatonischer Halbton.

pythagoreisch	Rein
c-d=9k	c-d=9k (⁹/₈)
d-e=9k	d-,e=8k (¹⁰/₉)
e-f=4k (²⁵⁶/₂₄₃)	,e-f=5k (¹⁵/₁₆)
f-g=9k	f-g=9k
g-a=9k	g-,a=8k,
a-h=9k	,a-,h=9k
h-c=4k	,h-c=5k

Intervalle werden hier addiert, zum Beispiel hat die Quinte die Größe
c-g=(c-d)+(d-e)+(e-f)+(f-g)=9k+9k+4k+9k=31k. Zweite Rechnung
c-g=(c-d)+(d-,e)+(,e-f)+(f-g)=9k+8k+5k+9k=31k.
Hier sind die Quinten c-g, g-d und f-c mit 31k in pythagoreischen und reiner Stimmung rein (Frequenzverhältnis ³/₂), die Terzen c-e / f-a und g-h mit 18k pythagoreisch (Frequenzverhältnis ⁸¹/₆₄) und die Terzen c-,e / f-,a und g-,h rein (Frequenzverhältnis ⁵/₄). Die Oktave c-c besteht aus 53 Teilen: Oktave = 53k (Frequenzverhältnis ²/₁).
Oft wird auch mit Cent gerechnet, wobei Oktave = 1200 Cent. Die Rechnungen mit dem Mercatorkomma k sind aber einfacher und übersichtlicher!
Man sieht hier: Intervalle kann man addieren reine große Terz=c-,e = 9k+8k = 17k (⁵/₄). Die Frequenzverhältnisse müssen multipliziert werden: ⁹/₈•¹⁰/₉ = ⁵/₄.

Das ist schon alles, was Sie über die reine Stimmung wissen müssen. Die Besonderheiten der reinen Stimmung sind:

Bei Modulationen ändern sich in reiner Stimmung nicht nur Töne mit Vorzeichenwechsel, sondern auch Töne um ein Komma. Zum Beispiel ist in in G-Dur das Intervall g-a=9k (nicht mehr 8k) und in F-Dur das Intervall c-,d = 8k (nicht mehr 9k), da jede reine Dur-Tonleiter den Aufbau 9k-8k-5k-9k-8k-9k-5k hat.
G-Dur: g-a=9k / a-,h=8k /,h-c=5k / c-d=9k / d-,e=8k / ,e-,fis=9k / ,fis-a=5k.
F-Dur: f-g=9k / g-,a=8k /,a-b=5k / b-c=9k / c-,d=8k / ,d-,e=9k / ,e-f=5k.
Um alle Tonleitern des Quintenzirkels rein spielen zu können, reicht es nicht aus, dass man Halbtöne zwischen die Ganztöne einer Tastatur zu einer 12-er Tastatur ergänzt, da sich Töne nicht nur um ein Vorzeichen unterscheiden, sondern auch um ein Komma. Man kämpfte lange Zeit daher um eine Temperierung dieser 12 Töne. Heute verwenden wir die gleichstufige Stimmung, bei der die Quinten im Quintenzirkel um ¹/₁₂ Komma vermindert werden, damit der Quintenzirkel aufgeht (siehe unten pythagoreisches Komma). Jeder Halbton hat hier die Größe von ¹/₁₂ Oktave = 4⁵/₁₂k. Aber diese Stimmung hat keine gute Intonation.
Der Cellist Pablo Casals schreibt dazu in The Way They Play (1972).
Erschrick nicht, wenn Du eine andere Intonation als das Klavier hast. Das liegt am Klavier, das verstimmt ist. Das Klavier mit seiner gleichstufigen Stimmung ist ein Kompromiss in der Intonation.

reine Stimmung

gleichstufiger Stimmung

Bei reiner Stimmung hören Sie keine Schwebungen, bei gleichstufiger Stimmung einen getrübten Klang wegen der "Verstimmung" der Terz.
In der gleichstufigen Stimmung erklingt die große Terz noch um ²/₃k (14 Cent) zu groß. Und das ist zu viel, wird aber heute bei 12-stufigen Tasteninstrumenten toleriert.

Die gute Nachricht

Wenn Musiker und Sänger auf einander hören, gelingt die gute Intonation von selbst. Man entwickelt schnell ein Gefühl für "tonales" Hören.
Es genügt zu wissen, dass das Klavier mit seiner gleichstufigen Stimmung ein Kompromiss in der Intonation ist. Aber selbst dort hört man sich die Akkorde zurecht.

Die pythagoreische Stimmung

Im Abschnitt über die reine Stimmung wurde schon die pythagoreische Stimmung angesprochen. Diese will ich hier kurz erklären.
Im Früh- und Hochmittelalter verwendete man in den Kirchentonarten nur die Töne A B/H C D E F G, wobei die Änderung von H in B erlaubt war. Auf der Orgel wurden sie mit reinen Quinten nach Gehör gestimmt. Da es keinen Kammerton gab, musste man oft bei Zusammenspiel zum Beispiel mit Blasinstrumenten transponieren. Deshalb fügte man weitere Halbtöne zum Beispiel Cis, Es, Fis und Gis ein. Man erhielt so die 12-stufige Tastatur:

C-Cis=5k

C-D=9k

D-Es=4k

D-E=9k
E-F=4k

F-Fis=5k

F-G=9k

G-Gis=5k

G-A=9k

A-B=4k

A-H=9k
H-C=4k
Die diatonischen Halbtöne haben hier die Größe von 4k (z.B. D-Es oder E-F), die chromatischen Halbtöne die Größe von 5k (z.B. C-Cis).

Wie stimmte man damals

Man stimmte damals nach Gehör. Jeder Geigenspieler weiß, dass man reine Quinten exakt mit dem Gehör stimmen kann. Damals stimmte man Instrumente mit 12 Tasten mit 11 reinen Quinten Es-B-F-C-G-D-A-E-H-Fis-Cis-Gis (und mit Oktaven). Bei der 12. Quinte Gis-Dis war die Taste für Dis schon mit Es bestzt. Wurde die 12. Quinte Gis-Dis mit Gis-Es gespielt, ergab sich eine "Wolfsquinte". Sie heulte wie ein Wolf, da das Es ein pythagoreisches Komma zu tief war.

Das pythagoreische Komma

Geht man vom Ton c 12 Quinten (immer wieder oktaviert) nach oben c g d a e h fis cis gis dis ais eis his so landet man bei einem Tasteninstrument auf dem selben Ton c. In Wahrheit handelt es sich jedoch bei diesem Ton um his und dies ist in seiner Tonhöhe um das pythagoreische Komma höher als c. Das pythagoreische Komma ist nahezu so groß wie das Mercator-Komma k.
Rechnung. Die Quinte, zum Beispiel c-g, hat die Größe von 31k, zwölf Quinten also 12•31k. Man hat dabei 7 Oktaven übersprungen. Geht man diese zurück, so erhält man
pythagoreisches Komma = 12•31k-7•53k = k.

Mit der Kenntnis dieses Kommas ist für viele Musiker die Geschichte zu Ende.
Dabei ist wegen der reinen großen Terz das syntonische Komma ausschlaggebend.

Das syntonische Komma

Das Intervall "vier Quinten aufwärts und zwei Oktaven abwärts" zum Beispiel c g d a e ist ein Intervall, das sich von der reinen Terz c-,e um das syntonische Komma unterscheidet.
Rechnung: 4Quinten aufwärts, 2 Oktaven zurück: 4•31k-2•53k =k.

Wer nicht mit Mathematik (Logarithmen usw.) belästigt werden will, kann ohne Verständnisschwierigkeiten weiter zu Modulationen. Es genügt zu wissen:

Einfach genial: Die Mercatorrechnungen sind viel einfacher und doch genau genug.

Allerdings: Das pythagoreische Komma ist ein Cent (eine Winzigkeit) größer als k und das syntonische Komma ein Cent tiefer als k.

Genauigkeit der Mercator-Rechnung

Die heutigen Musiktheoretiker rechnen mit Frequenzverhältnissen, Logarithmen und der Einheit Cent. Das macht den Vergleich von Intervallen unanschaulich. Auch Werte in Cent kann man sich schlecht merken.
Beispiel (lb=Logarithmus zur Basis 2; Oktave = 1200 Cent):

Intervall	Größe nach Mercator	Größe in Cent
reine große Terz	17k	1200•lb(5/4)=386 Cent
pythagoreische Terz	18k	1200•lb(81/64)=408 Cent

Die pythagoreische Terz ist also ein Komma größer als die reine Terz. Sie sehen hier:
Viel anschaulicher und einprägsamer ist die Größenangabe von Intervallen als Vielfache des Mercatorkommas k.
Hier müssen wir Rechnungen durchführen, die bei der Mercatorechnung vermeidbar sind.
Rechnet man mit Frequenzverhältnissen und den logarithmischen Größenangaben in Cent (Oktave = 1200 Cent, Halbton=100 Cent, lb: Der Logarithmus zur Basis 2), so erhält man:
pythagoreisches Komma=12Quinten-7Oktaven ⇒ Frequenzverhältnis=(³/₂)¹²:2⁷=⁵³¹⁴⁴¹/₅₂₄₂₈₈, ⇒ pythagoreisches Komma =1200*lb(⁵³¹⁴⁴¹/₅₂₄₂₈₈)Cent=23,5 Cent.
syntonisches Komma=4 Quinten-2Oktaven-reine Terz. Frequenzverhältnis=(³/₂)⁴:2²:(⁵/₄)=⁸¹/₈₀ ⇒ syntonisches Komma=1200*lb(⁸¹/₈₀)=21,5 Cent.
Das Mercatorkomma mit k=1200:53 Cent= 22,6 Cent liegt dazwischen.
Die mercatorrechnung, die die komplizierten Rechnungen mit dem Frequenzverhältnissen und Logarithmen vermeidet, ist also nicht ganz genau, seine Größenangaben der Intervalle sind aber mehr als ausreichend. Der Unterschied von 1 Cent ist vernachlässigbar. Und der große Vorteil der Mercatorrechnung ist: Ohne Logarithmen wird ihre Größe angegeben und man kann sie addieren.

Für Mathematiker:
Die reine Terz nach mercator: c-,e=9k+8k=17k=17 •¹²⁰⁰/₅₃Cent=385 Cent.
Der exakte Wert ist 1200 •lb(5/4)Cent=386 Cent.
Die reine Quinte nach Mercator: c-g=9k+8k+5k+9k=31k=31 •¹²⁰⁰/₅₃Cent=702Cent.
Der exakte Wert ist 1200 •lb(3/2)=702Cent. Hier noch weitere Werte:

Intervall	Größe (nach Mercator)	In Cent	Frequenzverhältnis	exakter Wert in Cent
diatonischer Halbton	5k	113	¹⁵/₁₆	112
Kleiner Ganzton	8k	181	¹⁰/₉	182
Großer Ganzton	9k	204	⁹/₈	204
Kleine Terz	14k	317	⁶/₅	316
Große Terz	17k	385	⁵/₄	386
Quarte	22k	498	⁴/₃	498
Tritonus	26k	589	⁴⁵/₃₂	590
Quinte	31k	702	³/₂	702

Die Näherungen nach Mercator sind also bis auf 1 Cent genau und viel viel anschaulicher.

Die Eulerschreibweise

Wir haben oben gesehen, dass das Intervall "vier reine Quinten aufwärts und zwei Oktaven abwärts"

zum Beispiel c-g-d-a-e das Intervall c-e die pythagoreische Terz ergibt, das um ein (syntonisches) Komma zu hoch im Vergleich zur reinen Terz ist. Damit man eine reine Terz erhält, muss man e um ein Komma erniedrigen. Dieses e wird notiert als ,e ("Tiefkomma e"). Damit ist das Intervall c-,e eine reine Terz.

In der C-Dur-Tonleiter sind auch die Intervalle f-,a und g-,h reine große Terzen.
Die reine C-Dur-Tonleiter ist dann: c-d-,e-f-g-,a ,h-c.
Die Quinten ... es b f c g d a e h fis ... sind in dieser Schreibweise reine Quinten.
Die Quinten ... ,es, b ,f ,c ,g ,d ,a ,e ,h ,fis ... mit dem Tiefkomma alle jeweils ein Komma tiefer,
die Quinten ... 'es 'b 'f 'c 'g 'd 'a 'e 'h 'fis ... mit dem Hochkomma alle jeweils ein Komma höher.
Das Hochkomma wird zum Beispiel beim Mollakkord c-'es-g benötigt.

Modulationen

Die C-Dur-Tonleiter lautet in Eulerschreibweise.
c d ,e f g ,a ,h c (Zur Schreibweise: ,e ist ein Komma tiefer wie e usw.) Die G-Dur-Tonleiter

g a ,h c d ,e ,fis g

Was hat sich im Vergleich zur C-Dur-Tonleiter geändert?
f in ,fis -das lernt man im Unterricht - und ,a in a -das ist im Notenbild nicht erkennbar.

Wenn rein intoniert wird muss bei dieser Modulation ,a um ein Komma zu a erhöht werden. Eine geringfügige Änderung des Tones, spielt aber beim Wohlklang von Akkorden eine große Rolle.
Hören Sie hier genau hin. Hören Sie den Unterschied von ,a in C-dur und a in G-Dur.
Spiele in C-Dur:

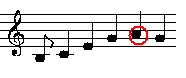
Spiele in G-Dur: Hören Sie den feinen Unterschied?

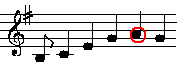
Und jetzt dasselbe mit Akkorden:
Spiele in C-Dur:

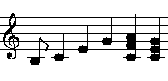
Spiele in G-Dur:

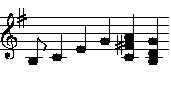
Zum Vergleich:
Spiele a' in C-Dur (440 Hz), in G-Dur (445,5Hz) und beide und zusammen

Die mitteltönige Stimmung

Wir haben gesehen: Die reine C-Durtonleiter hat die Form:
c-d=9k / d-,e=8k / ,e-f=5k / f-g=9k / g-,a=8k / ,a-,h=9k und ,h-c=5k. (k ist das Mercatorkomma).
Die reinen großen Terzen (Frequenzverhältnis ⁵/₄) sind dann c-,e=17k, f-,a=17k und g-,h=17k sowie die reinen Quinten (Frequenzverhältnis ³/₂) c-g=31k, f-c=31k und g-d=31k und die reine Oktave (Frequenzverhältnis ²/₁) c-c=53k.
Wenn wir nun, um weitere Tonleitern spielen zu können, weitere Halbtöne dazwischen einfügen, kommt das System sofort durcheinander, da sich die Ganztöne (groß=9k, klein=8k) bei Modulationen verändern. (Theoretische entstehen die beiden verschiedenen Ganztöne durch Überlegungen in der Harmonik. In Melodien kann der Unterschied vernachlässigt werden.)
Bei der mitteltönigen Stimmung werden diese Ganztöne gemittelt.
Wir erweitern hier die Eulerschreibweise: Die Schreibweise mit dem Tiefpunkt vor der Tonbezeichnung .g bedeutet, dass g um ¹/₄k erniedrigt wird. Mit Hochpunkt davor, zum Beispiel °f, bedeutet, dass f um ¹/₄k erhöht wurde.

Die C-Dur-Tonleiter lautet dann:
c-..d=8¹/₂k
..d-,e=8¹/₂
,e-°f=5¹/₄k
°f-.g=8¹/₂k
.g-...a=8¹/₂k
...a-.,h=8¹/₂k
.,h-c=5¹/₄k
Die Halbtöne ,e-°f und .,h-c mussten hier noch um ¹/₄k vergrößert werden, damit die Oktave c-c rein mit 53k erklingt.
Bei dieser Einteilung sind die großen Terzen c-,e, °f-...a und .g-.,h rein, die Quinten
°f-c=c-.g=.g-..d=..d-...a=...a-,e=,e-.,h=30³/₄k groß (also ¹/₄k kleiner als die reine Quinte).

Bei der mitteltönigen Stimmung werden noch Halbtöne folgendermaßen eingefügt:
c-..d=8¹/₂k

...,cis-..d=5¹/₄k
..d-°°°es=5¹/₄k

..d-,e=8¹/₂,
,e-°f=5¹/₄k,
°f-.g=8¹/₂k,

..,fis-.g=5¹/₄k

.g-...a=8¹/₂k,

,,gis-...a=5¹/₄k
...a-°°b=5¹/₄k

...a-.,h=8¹/₂k
.,h-c=5¹/₄k.
Bei dieser mitteltönigen Stimmung auf unserer 12-stufigen Tastatur sind wie C-Dur auch folgende sechs Tonarten bis auf die leicht verstimmten Quinten rein: B-Dur, F-Dur, C-Dur, G-Dur, D-Dur und A-Dur.

Wie stimmte man damals mitteltönig ein

Die 4 Quinten c-g, g-d, d-a und a-e (siehe Hörbeispiel oben) wurden nicht rein, sondern etwa verkleinert so eingestimmt, dass die Terz c-e rein erklang. Die Schwebungen dieser Quinten wurden mit Hilfe des Herzschlages abgeschätzt. Die übrigen Töne konnten dann mit folgenden reinen Terzen (und Oktaven) eingestimmt werden: b-d, f-a, d-fis, a-cis und e-gis.
Bei dieser Stimmung ergab sich im Quintenzirkel es-b-f-c-g-d-a-e-h-fis-cis-gis, dass die 11 Quinten alle um ¹/₄ Komma kleiner sind als reine Quinten. Die zwölfte Quinte gis-dis musste als Wolfsquinte gis-es gepielt werden, die 2 Kommata zu klein wie ein Wolf heulte.

Diese mitteltönige Stimmung war in der Renaissance, im Barock und vielfach auch in späterer Zeit (bis in das 19. Jahrhundert) für Tasteninstrumente gebräuchlich. Man konnte so die Tasteninstrumente relativ leicht einstimmen. Mit der Zeit wurden die Modulationen aber verwegener und da stellte sich heraus: Es gibt zum Beispiel bei As-Dur Missklänge, denn die Tastatur war auf gis gestimmt und man konnte as nicht mit gis enharmonisch verwechseln.

Begründung: Die diatonischen Halbtöne unterscheiden sich bei der mitteltönigen Stimmung von den chromatischen um 2k.
Es ist g-a=8¹/₂k, der diatonische Halbton gis-a=5¹/₄k, also der chromatische Halbton g-gis=8¹/₂k-5¹/₄k=3¹/₄k. Es müsste aber sein g-as=5¹/₄k. Aber für as ist auf einer 12-stufigen Tastatur kein Platz.

Hörbeispiel: Kadenzen F-Dur und As-Dur:

In mitteltöniger Stimmung wird statt 'As und °'Des das um 2k tiefere ,,Gis bzw. ...,Cis gespielt.

Wohltemperierte Stimmungen

Um diesen Nachteil auszugleichen, veränderte man die Stimmung auf Kosten der reinen Terz in C-Dur-fernen Tonarten. Es gibt unzählige Variationen dieser wohltemperierten Stimmungen. Dadurch bekamen die Tonarten verschiedenartige Färbungen, als Tonartencharakteristik bezeichnet.

Man muss bedenken, dass bis ins 18 Jahrhundert mit dem Gehör gestimmt werden musste. Die Qualität von verkleinerten Quinten oder vergrößerten Terzen konnte man durch Auszählen der Schwebungen abschätzen. Die theoretisch bekannte gleichstufige Stimmung mit 12 gleichen Halbtönen war nicht gebräuchlich (Mit Ausnahme von einigen Lauten, bei der der Stegabstand geometrisch berechnet werden konnte.) Welche Stimmung J.S. Bach verwendete ist nicht bekannt. Er stimmte sein Clavichord in 15 Minuten. Seine Stimmung war wohl ähnlich zur folgender wohltemperierten Stimmung, genannt Werckmeister III. 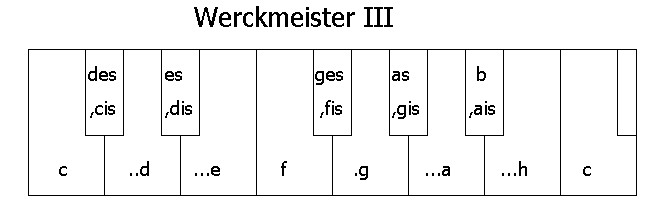tastatur_werckmeister3

c-,cis/des=4k,

c-..d=8¹/₂k,

..d-,dis/es=4¹/₂k,

..d-...e=8³/₄k,
...e-f=4³/₄k,

f-,fis/ges=4k,

f-.g=8³/₄k
.g-...a=8¹/₂k,

...a-,ais/b=4³/₄k,

...a-...h=9k und
...h-c=4³/₄k.

Bei dieser Stimmung klingen C-Dur-nahe Tonleiter reiner als die übrigen, so dass sich eine Tonartencharakteristik ergibt.
Viele Orgeln sind auch heutzutage noch wohltemperiert gestimmt, so dass die Tonartencharakteristik erhalten bleibt, was bei der gleichstufigen Stimmung nicht mehr der Fall ist.
Weitere wohltemperierte Stimmung: siehe Terzorientiert wohltemperiert und hier...

Hinweis: Ganz genau genommen unterscheiden sich die hier erwähnten gleichgesetzten Töne ,cis=des / ,dis=es / ,fis=ges und ,ais=b um das Schisma, ein Intervall von 2 Cent, von dem Musiktheoretiker Andreas Werckmeister so genannt und als so geringfügig betrachtet, dass dieser Unterschied völlig vernachlässigbar ist.

Beurteilung dieser Stimmung

Vor allem spielen die großen Terzen eine Rolle (rein=17k, gleichstufig 17²/₃k, pythagoreisch=18k)
es-.g=17³/₄k
b-..d=17¹/₂k
f-...a=17¹/₄k
c-...e=17¹/₄k
.g-...h=17¹/₂
..d-,fis=17¹/₂k
...a-,cis=17³/₄k
...e-,gis=17³/₄k
...h-,dis=17³/₄k
,fis-,ais=ges-b=18k
des-f=18k
as-c=18k

Kadenzen in Werckmeister III-Temperatur

Zuerst in C-Dur, dann in E-Dur und Cis-Dur mit geschärften Terzen mit 17³/₄k=402 Cent und 18k=408 Cent.
kadenzen_c_dur_e_dur_cis_dur

Die gleichstufige Stimmung

Die gleichstufige Stimmung ist die heute übliche Stimmung unserer Klaviere usw. Zu Zeiten, als man ohne technischen Hilfsmittel mit dem Gehör stimmen musste, war dies ein schwieriges Unterfangen. Erst im 20. Jahrhundert setzte sie sich durch. Bei dieser Stimmung wird die Oktave mit 53k einfach in 12 gleiche Teile geteilt. Diese Stimmung wird dann folgendermaßen dargestellt: (Wir verlassen hier die Eulerschreibweise.)

c-cis/des=4⁵/₁₂k,

c-d=8⁵/₆k,

d-dis/es=4⁵/₁₂k,

d-e=8⁵/₆k
e-f=4⁵/₁₂k,

f-fis/ges=4⁵/₁₂k,

f-g=8⁵/₆k,

g-gis/as=4⁵/₁₂k,

g-a=8⁵/₆k,

a-ais/b=4⁵/₁₂k,

a-h=8⁵/₆k,

h-c=4⁵/₁₂k.
Alle Ganztöne haben die Größe von =8⁵/₆k=1200/53•8⁵/₆Cent=200Cent, alle Halbtöne die Größe =4⁵/₁₂k=100Cent.
Wie oben erwähnt ist diese Stimmung aber nicht für den A-Cappella-Gesang geeignet. Bei diesem kann man die Terzen rein intonieren, während diese bei der gleichstufigen Stimmung als rau empfunden werden. Gleichstufige Terzen können Sänger nicht intonieren.

Bei der gleichstufigen Stimmung werden die Quinten anpasst ... und damit ist die Geschichte für viele Schreiber und Musiker zu Ende - außer, dass dieses System der 12 gleichen Halbtöne auf schreckliche Weise die musikalische Harmonie vereinfacht

Zitiert nach Ross W.Duffin
Wie die gleichstufige Stimmung den Wohlklang zerstört (2007). Was Ross W. Duffin hier anspricht ist, dass viele meinen, mit Kenntnis des pythagoreischen Kommas weiß man schon alles über die Stimmungen. Und das ist ein Irrtum. Die Intonation von Akkorden ist vielschichtiger. Vor allem spielt nach der Entdeckung der Mehrstimmigkeit die reine Terz die Hauptrolle.

Weiterlesen oder hören

Als Musiker genügt es zu wissen, dass es feine Unterschiede zum Klavier in der Intonation gibt. Der Musiker hört sich hinein.

Zum Verständnis der richtigen Intonation können Sie sich in weitere Hörproben vertiefen.

Um den Zusammenhang zwischen dem pythagoreischen und syntonischen Komma zu verstehen, können Sie die Lektionen studieren oder sich in den Schnellkurs (Musiktheorie, ziemlich abstrakt) vertiefen. In der Übersicht werden noch zahlreiche weitere musiktheoretische Themen abgehandelt. Bei allem spielt das syntonische Komma eine herausragende Rolle.

Schnellkurs

Lektionen zur reinen Stimmung

Lektion 1 Töne, Intervalle, Frequenzen und Frequenzverhältnisse
Lektion 2 Hintereinanderausführung zweier Tonschritte. Reine Stimmung
Lektion 3 Beschreibung von Tonsystemen ohne Akustik
Lektion 4 Das Centmaß für Intervalle
Lektion 5 Die gleichstufige Stimmung
Lektion 6 Das pythagoreische und syntonische Komma
Lektion 7 Eulersches Tonnetz - Modulationen
Lektion 8 Mitteltönige und wohltemperierte Stimmungen
Lektion 9 Akkord der 2. Stufe, die Kommafalle, neapolitanischer Sextakkord, Doppeldominante

Und noch viel mehr

Unterschied zwischen verminderter Terz und Ganzton

und so weiter

Mit Hilfe des Programm Musik, das Feinmodulationen hörbar und durch die gleichzeitige Berechnung der Frequenzverhältnisse auch sichtbar macht, kann man Intonationen vergleichen:

Mit dem Programm TTTon, einem Tongenerator, können Sie Ihr Gehör oder Ihre Anlage prüfen und Schwingungsformen aufzeichnen.