Joachim Mohr Mathematik Musik

Kurzfassung: In Eulerschreibweise sind die Dreiklänge in reiner Stimmung von folgender Form:
Dur: x-,y-z bzw. ,x-,,y-,z. Zum Beispiel: c-,e-g oder ,e-,,gis-,h.
moll: x-'y-z bzw. ,x-y-,z. Zum Beispiel: c-'es-g oder ,e-g-,h.

Dabei handelt es sich bei der Quintenfolge ...b-f-c-g-d-a... um reine Quinten, bei der Quintenfolge ...,b-,f-,c-,g-,d-,a... mit dem Tiefkomma vor der Notenbezeichnung auch um reine Quinten, jedoch sind alle Töne ein syntonisches Komma tiefer, und bei der Quintefolge ...'b-'f-'c-'g-'d-'a... mit dem Hochkomma vor der Notenbezeichnung ebenfalls um reine Quinten, jedoch sind alle Töne ein syntonisches Komma höher als bei der ersten Quintenfolge.

Version 2019

Die Eulerschreibweise

Bisher quälte man sich mit Eulerschen "Tonnetzt" herum..
Sich in dieses zweidimensionale Geflecht einzulesen, ist obsolet.
Für die musikalische Feinanalyse genügt die Eulerschreibweise!

Was Sie über die Eulerschreibweise wissen müssen:
Ausgangspunkt ist die Kette aus reinen Quinten (Frequenzverhältnis ³/₂):
... des as es b f c g d a e fis cis ...
,a (434,6 Hz) ("Tiefkomma a") bedeutet a (440 Hz) um ein syntonisches Komma erniedrigt.
'as (422,4 Hz) ("Hochkomma as) bedeutet as (417,185) um ein syntonisches Komma erhöht.

Ich habe für die Besprechnung der mitteltönigen Stimmung noch folgende Bezeichnung verwendet:
.x (Tiefpunkt x) bzw. °k (Hochpunkt x) bedeutet: Der Ton x um 1/4 syntonisches Komma erniedrigt bzw. erhöht.

Dann ist zum Beispiel das Intervall f ,a eine reine große Terz (⁵/₄) und das Intervall f 'as eine reine kleine Terz (⁶/₅).

Für Mathematiker:
Frequenzverhältnis des syntonischen Kommas: ⁸¹/₈₀.
Frequenzverhältnis f:a=(³/₂)⁴:4=⁸¹/₆₄ (4 Quinten hoch, zwei Oktaven tief = pyth. große Terz.).
Frequenzverhältnis f:,a(f:Tiefkomma a)=⁸¹/₆₄:⁸¹/₈₀=⁵/₄.

Wie werden Intervalle nach Gehör intoniert? Mit dem Aufkommen der Mehrstimmigkeit in der zweiten Hälfte des 15. Jahrhunderts wird neben der Oktave und der Quinte auch die Terz rein intoniert.
In der reinen Stimmung wird das Stimmungssystem aufgebaut aus den Intervallen:

Oktave (Frequenzverhältnis 2 )
Quinte (Frequenzverhältnis ³/₂) und
große Terz (Frequenzverhältnis ⁵/₄).

Alle übrigen Intervalle sind Vielfache dieser drei Intervallen.

Wir betrachten die reine Quintenfolge:
... es(⁸/₂₇) b(⁴/₉) f(²/₃) c(1) g(³/₂) d(⁹/₄) a(²⁷/₈) e(⁸¹/₁₆) ... (In Klammer: Frequenzverhältnis zu c).
In einer Oktavlage (Die entsprechenden Frequenzverhältnisse mit Vielfachen von 2 multipliziert):
... es(³²/₂₇) b(¹⁶/₉) f(⁴/₃) c(1) g(³/₂) d(⁹/₈) a(²⁷/₁₆) e(⁸¹/₆₄) ...

(Für unsere Untersuchungen genügt es, alle Töne in einfacher Oktavlage zu schreiben, also nicht e' oder e'' für das eingestrichene oder zweigestrichene e usw.)

Das Intervall ce hat hier das Frequenzverhältnis ⁸¹/₆₄. Es handelt sich dabei um die pythagoreische Terz (diese klingt sehr rau). Wenn wir den Ton e um das syntonische Komma(⁸¹/₈₀) zu ,e ("Tiefkomma e") erniedrigen, erhalten wir mit dem Intervall c ,e(⁵/₄) die reine Terz.

Eulersche Schreibweise

Der Ton ,e ("Tiefkomma e", das Komma "," vor e) erklingt ein syntonisches Komma tiefer als e.
In der Literatur sieht man häufig die für uns satztechnisch unbequeme Schreibweise:

e ("e unterstrichen").
-

Begündung: Wird das Intervall ce(⁸¹/₆₄) um das syntonische Komma(⁸¹/₈₀) erniedrigt, so muss man die Frequenzverhältnisse dividieren:

81 81   81   80   80   5 
--:-- = -- . -- = -- = -.
64 80   64   81   64   4

Man erhält so das Intervall der reinen Terz c, e(⁵/₄).

Beachte: c ,e ist das Intervall von c nach ,e ("Tiefkomma e").

Alles, was Sie über die Eulersche Schreibweise wissen müssen:
Reine Quinten im Quintenzirkel: ... es b f c g d a e ...
Ein Terzkomma tiefer ... ,es ,b ,c ,g ,d ,a ,e ... (Tiefkomma vor der Tonbezeichnung)
Ein Terzkomma höher ... 'es 'b 'c 'g 'd 'a 'e ... (Hochkomma vor der Tonbezeichnung).

(In der Literatur wird dieser Sachverhalt oft zweidimensional als "Eulersches Tonnetz" dargestellt. Dies ist oft verwirrend und nicht mehr notwendig, wenn wir die Eulersche Schreibweise verwenden.)

Beispiel: Die reine C-Dur-Tonleiter lautet: c d ,e f g ,a ,h c.
Beispiel: Die reine c-moll-Tonleiter lautet: c d 'es f g 'as 'b c.
Beispiel: Die melodische a-moll-Tonleiter lautet ,a ,h c ,d e ,,fis ,,gis ,a.
Beachte: Reine Terzen sind c ,e oder ,c ,,e oder es ,g oder 'es g oder d ,fis oder ,d ,,fis usw.

Beispiel: Die A-Dur-Kadenz in Eulerschreibweise

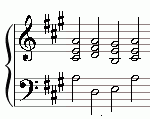
Akkorde (vertikal) a a ,gis a e ,fis e e ,cis d h ,cis a d e a
Spiele A-Dur-Kadenz

Die A-Dur-Tonleiter schreibt sich nämlich: a h ,cis d e ,fis ,gis a

Modulationen

Vergleicht man in der Eulerschreibweise
C-Dur c d ,e f g ,a ,h c mit
G-Dur g a ,h c d ,e ,fis g oder
F-Dur f g ,a b c ,d ,e f, so sieht man:

Ausführlich

Bei der Modulation in die Dominante ändern sich zwei Töne, einer im Notenbild sichtbar um einen Halbton (hier: f in ,fis), einer um ein syntonisches Komma (hier: ,a in a).

Spiele Modulation von C-Dur nach G-Dur

Im Streichquartett spielt die 1. Violine das zweite a ein syntonisches Komma höher. Ein Violinspieler weiß, dass er hier nicht die A-Saite zwei Mal spielen kann. Er muß das zweite a "expressiv" in Lage spielen.
Im Allgemeinen intoniert ein guter A-cappella-Chor die Intervalle auch in einer solchen Situation rein.

Bei der Modulation in die Subdominante ändern sich entsprechend zwei Töne, einer im Notenbild sichtbar um einen Halbton (hier: ,h in b), einer um ein syntonisches Komma (hier: d in ,d).

Weiterlesen: Der Quintenzirkel in reiner Stimmung
Modulationen in Eulerschreibweise (Mit 12-stufiger Skala)

Der Akkord der zweiten Stufe

Hier sieht man sehr schön, wie erhellend die Eulerschreibweise ist.

Betrachten wir C-Dur c d ,e f g ,a ,h c Lassen wir einmal die verminderte Quinte ,h f außer Acht, so sind alle Quinten der C-Dur-Tonleiter c g und ,e ,h und f c und g d und ,a ,e rein bis auf eine Ausnahme: Die Quinte d ,a ist in C-Dur unrein. Das d ist um ein syntonisches Komma zu hoch. Wenn ich d erniedrige zum ,d der a-moll-Tonleiter oder F-Dur-Tonleiter wird die Quinte ,d ,a rein.

Hören Sie selbst: Zuerst d ,a (rau klingende Schwebungen) und dann ,d ,a (Ohne Schwebungen):

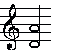Spiele d,a in C-Dur und ,d,a in F-Dur

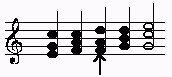In der Kadenz Akkord der 2. Stufe

ist der 3. Akkord f ,a ,d F-Dur zuzuordnen, der 4. Akkord g h d dagegen wieder als Dominante von C-Dur.
Spiele:

Man hört: Im 4. Akkord ist d höher (expressiver) als das ,d im 3. Akkord

Als Chorleiter muß man darauf achten, dass das d im 4. Akkord, das im Akkord zuvor um ein Komma als ,d tiefer intoniert wurde, ein höheres d ist. Der Sopran muss im 4. Akkord das d als reine Quinte zu g intonieren. Wenn man in einem Chor, der auf einander hört, darauf hinweist, wird richtig intoniert. Mit einem Sopran, der stur die Tonhöhe von ,d hält, tappt in die Kommafalle.

Für Mathematiker

Wie berechnen sich die Frequenverhältnisse, oder besser die Differenz zu c in Cent der
C-Dur-Tonleiter c d ,e f g ,a ,h c und der
c-Moll-Tonleiter c d 'es f g 'as 'b c
erweitert um weitere chromatische Töne so, dass die Intervalle c 'des sowie ,cis d usw. diatonische Halbtöne (Frequenzverhältnis ¹⁶/₁₅) sind.
Mit der Eulerschreibweise ist dies leicht durchzuführen.

Zunächst: Die Quintenkette

ces ges des as  es  b   f   c
 -7  -6  -5 -4  -3 -2  -1   0
c   g   d   a   e   h   fis cis gis dis ais eis his 
0   1   2   3   4   5   6   7   8   9   10  11  12

Das Frequenzverhältbis von c zu as ist zum Beispiel (2/4)^-4 = ¹⁶/₈₁, drei mal oktaviert ¹²⁸/₈₁, der Abstand 1200*lb(128/81) Cent = 792,18 Cent, das Frequenzverhältnis von c zu 'as entsprechend ¹²⁸/₈₁*⁸¹/₈₀ = ⁸/₅ (kleine Sext), der Abstand 813,69 Cent.

Mit Oktave = 1200 Cent, Quinte = 1200*lb(³/₂) Cent = 701,96 Cent und syntonisches Komma = 1200*lb(⁸¹/₈₀) = 21,51 Cent berechnet sich.

pythagoreisch

c(0) 

cis(113,69)  
des(90,22)    
   
d(203,91) 

dis(317,60) 
es(294,13)   

e(407,82) 
fes(384,36)  

eis(521,51) 
f(498,04)    

fis(611,73) 
ges(588,27)  

g(701,96) 

gis(815,64) 
as(792,18)   

a(905,87) 

ais(1019,55) 
b(996,09)    

h(1109,78) 
ces(1086,31) 

his(1223,46) 
c(1200)

Rein

c(0) 

,cis(92,18) 
'des(111,73) 

d(203,91) 

,,dis(274,58) 
'es(315,64) 

,e(386,31) 
''fes(427,37) 

,,eis(478,49)
f(498,04) 

,fis(590,22) 
'ges(609,78)

g(701,96) 

,,gis(772,63) 
'as(813,69) 

,a(884,36) 

,,ais(976,54) 
'b(1017,60) 

,h(1088,27)  
''ces(1129,33) 

,,his(1180,45) 
c(1200)

Intervall

Prim

gr. chrom. Halbton
diatonischer Halbton 

gr. Ganzton 

überm. Sekunde
kl. Terz 

gr. Terz
verm. Quarte 

gr. überm. Terz
Quarte 

überm. Quarte
kl. verm. Quinte

Quinte

kl. überm. Quinte
kl. Sext 

gr. Sext 

gr. überm. Sext
gr. kl. Septime 

gr. Septime
gr. verm. Oktave 

gr. überm. Septime
Oktave

Betrachten wir im folgenden die in der 12-stufigen Tastatur "gleichen" Töne, die verminderten Sekunden:
In der pythagoreischen Stimmung ist cis höher als des, dis höher als es, e höher als fes usw. (Der Unterschied ist das pythagoreische Komma = 23,46 Cent).

Dagegen ist in der reinen Stimmung ,cis tiefer als des und ,,dis tiefer als 'es une ,e tiefer als ''fes usw. (Der Unterschied ist: 2*syntonisches Komma - pythagoreisches Komma = 19,55 Cent (Diaschisma) bzw. 3*syntonisches Komma - pythagoreisches Komma = 41,06 Cent (kleine Diesis).

Für historisch interessierte Musiker

Ein "Archicembalo" benötigt 33 Tasten für eine Oktave, wenn darauf alle Tonarten des Quintenzirkel von Des-Dur bis Cis-Dur und die dazu Terzverwanden Tonarten von ,B-Moll/Dur bis ,Gis-Moll/Dur rein spielbar sein sollen.
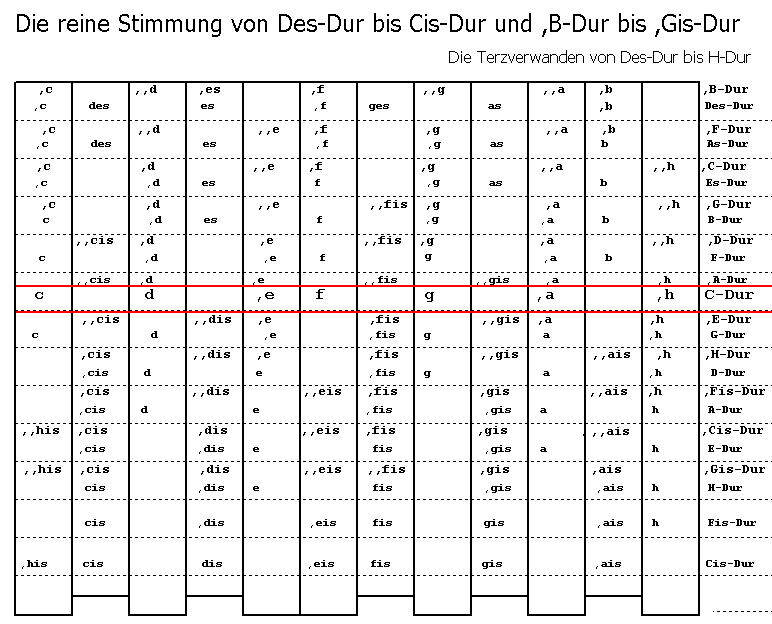
Tabelle aller reinen Tonleitern

Wenn man den Unterschied von einem Schisma vernachlässigt, benötigt man folgende Anzahl von Tasten:

(s=pythagoreisches Komma - syntonisches Komma = 1,95 Cent = Schisma)

C-Taste: 2, da ,his=c+s
Cis/Des-Taste: 3, da ,cis=des+s
D-Taste: 3
Dis/Es-Taste: 3, da ,,dis=,es+s und ,dis=es
E-Taste: 3
F-Taste: 2, da ,,e=,f+s und ,e=f+s
Fis/Ges-Taste: 3, da ,fis=ges+s
G-Taste: 3
Gis/As-Taste: 3, da ,gis=as+k
A-Taste: 3
Ais/B-Taste: 2, da ,,ais=,b+s und ,ais=b+s
H-Taste: 3

Insgesamt 33 Tasten