Siehe auch Neue Version
wie in Wikipedia
Mathematische Beschreibung von Tonsystemen
Im Folgenden wird die zugrundeliegende Theorie erläutert. Dies ist neben der Anschaulichkeit für die Interpretation historischer Tonsystembeschreibungen wichtig.
Zusammenfassung
Vom hörpsychologischen Standpunkt aus kann man feststellen:
- Die Intervalle des Tonraums sind geordnet, d.h. sie können der Größe nach verglichen werden ("Die Quinte ist kleiner als die Oktave").
- Die Hintereinanderausführung führt zu einer Addition ("Große Terz + kleine Terz = Quinte").
- Die Oktave kann als Einheit verwendet werden, d.h. jedes Intervall kann als Vielfaches der Oktave bzw. als Vielfaches der Untereinheit Cent angegeben werden. (Da 12 Quinten ungefähr 7 Oktaven ergeben, gilt Quinte ≈ 7/12 Oktave = 700 Cent.)
Es handelt sich hier um eine Vereinfachung eines Systems von Winfried Neumaier und ist dort als Anhang in seinem Buch "Was ist ein Tonsystem" veröffentlicht. Ein am mathematischen Institut in Tübingen im Dezember 1996 gehaltener Vortrag wird hier in überarbeiteter Version vorgestellt.
Einleitung
Der Ton- und Intervallraum als mathematische Struktur
Töne sind hörbar. Von diesem unmittelbares sinnliches Erlebnis gehen wir aus ... ohne Messinstrumente (mit Ausnahme der Stimmgabel). Uns genügt, was wir hören. Wir lassen uns wie ein Sänger nur von unserem Gehör leiten. Das Wissen von Tönen und Intervallen kann weitervermittelt werden.
Intervalle sind als Klang wahrnehmbar, eng verbunden mit zwei Tönen. Wir führen für das Intervall i, das durch zwei Töne A und B bestimmt ist, die Bezeichnung i = AB ein. Wenn Sie zum Beispiel zuerst eine große Terz gT auf dem Ton Des intonieren und anschließend auf dem Endton F eine kleine Terz kT, dann landen Sie bei As. Nach der nun folgenden Bezeichnung haben Sie zwei Intervalle addiert und eine Quinte Q erhalten: As = (Des + gT) + kT= Des + (gT+kT) = Des + Q mit Q = gT + kT.
Wir betrachten:
Die Menge der Töne T
Bezeichnung für Töne (oder Tonhöhen): A,B, ...zum Beispiel: A=Des B=As
und die Menge I der Intervalle
Intervalle bezeichnen wir mit i, j, ...
zum Beispiel i=gT (große Terz), j=kT (kleine Terz)
Sind A und B zwei Töne, so bestimmen sie eindeutig ein Intervall i.
Wir schreiben dafür: i=AB (A "Grundton", B "Endton").
zum Beispiel ist für A=Des und B=As die Quinte Q=AB bestimmt.
Ist umgkehrt der Grundton A und das Intervall i bekannt, so ist durch i=AB der Endton B eindeutig bestimmt.
Wir schreiben dafür B=A+i. (B Ton, i Intervall)
Intervalle kann man nach folgender Vorschrift addieren:
Ist i=AB und j=BC, dann sei i+j = AC.
Das bedeutet: Singe ich zuerst auf dem Grundton A das Intervall i bis zum Endton B und dann auf dem Grundton B das Intervall j bis C, dann ist das Intervall k=AC eindeutig bestimmt und werde mit i+j bezeichnet: k = i+j.
zum Beispiel gT + kT = Q (Große Terz + kleinen Terz = Quint).
Schließlich kann man Intervalle vergleichen.
Wir schreiben i ‹ j ("i kleiner als j") wenn der Endton von j höher als der Endton von i bei gleichem Grundton ist.
zum Beispiel Q ‹ Ok (Quint < Oktav) oder 2Q › Ok (Zwei Quinten › Oktav), wobei wie üblich 2Q=Q+Q bedeutet.
Damit haben wir eine mathematische Struktur (T,I,+,<) für den Tonraum eingeführt (siehe Axiomensystem ).
Ein Größenmaß für Intervalle
Wir benötigen noch eine Grundtatsache, das Oktavaxiom: Es gibt noch das vom Nullintervall verschiedene Intervall der Oktave.
Weitere Intervalle können mit der Oktave beliebig genau verglichen werden.
Beispiel: Q=Quinte und Ok=Oktave=1200 Cent. Immer bessere Annäherung sind:
Q‹Ok
2Q›Ok Unterschied: Ganzton
5Q‹3Ok Unterschied: Halbton
12Q›7Ok ⇒ Q≈7/12Ok=700 Cent. Unterschied: pythagoreisches Komma.
41Q‹24Ok ⇒ Q≈24/41Ok=702 Cent
53Q‹31Ok ⇒ Q≈31/53Ok=701,9 Cent
Quelle: Neumaier S.43
Diese Vergleiche sind mit dem Gehör noch nachprüfbar, der letzte gerade noch beim Cembalo durch genaues Stimmen. Hier stoßen wir an die Grenzen unseres musikalischen Hörvermögens. Zur Berechnung nehmen wir nun das Frequenzverhältnis 3/2 der Quinte und 2 für die Oktave zu Hilfe.Mathematisch formuliert: Q=sup{n/m|mQ‹nOk}Ok= sup{n/m|(3/2)m‹2n}Ok =log2(3/2)ok=701,9550Cent.
(Man sucht immer bessere Annäherungen für mQ‹nOk. Der "Grenzwert" dieser Brüche n/m wird mit dem Logarithmus zur Basis 2 berechnet:
Q = 1200×log2(3/2) Cent = 701,9550 Cent.
Der zwölfstufige Tonraum
Der Intervallraum I des zwölfstufigen Tonraumes wird mit Hilfe des Halbtons H mit 12H=Ok definiert.I={n·H| nεZ} (jedes Intervall ist ein Vielfaches von H) Dabei ist Z= Menge der ganzen Zahlen.
Dieses System ist mathematisch sehr einfach. Vom Hören kann man es jedoch nicht erschließen, wenn wir nicht Tongenerator und Logarithmentafel oder ähnliches zu Hilfe nehmen.
Vom Singen, Geigen- oder Trompetenspiel usw. her gesehen ist die gleichmäßige Einteilung der Oktave in zwölf gleiche Intervalle alles andere als trivial ... es ist ein Artefakt.
Es ist die Grundlage der gleichstufigen Stimmung, die heutzutage bei 12-stufigen Tasteninstrumenten verwendet wird.Das Quintsystem (pythagoreische Stimmung)
Der Intervallraum kaum wird von der Quinte Q und Oktave Ok erzeugt.I= {n·Q+m·Ok| n,mεZ} = Z·Ok + Z·Q
(Jedes Intervall ist eindeutig als Linearkombination von Q und Ok darstellbar)
Hier sind folgende Intervalle definierbar.
Ganzton=G=2Q-Ok (9/8 ≙ 204 Cent)
Ditonos=2G=4Q-2Ok (81/64 ≙ 408 Cent)
Quart=q=Ok-Q (4/3 ≙ 498 Cent)
Leimma=L=q-2G (256/243 ≙ 70 Cent)
Apotome=Ganzton-Leimma=G-L (2187/2048 ≙ 90 Cent)
pyth. Komma=12Q-7Ok=Apotome-Leimma (531441/524288 ≙ 23 Cent)
Daraus lässt sich eine Tonleiter bauen, das (pythagoreische) diatonische Tongeschlecht.
c d e f g a h c, wobei die aufeiander folgenden Intervalle sind:
c-d=d-e=f-g=g-a=a-h=G (Ganzton) und e-f=h-c=l (Leimma).
In der Gregorianik und frühen Zweistimmigkeit war diese Intonation vorherrschend.
Quinten klingen in dieser Intonation rein. Die Terz, der Ditonos, klingt dissonant (scharf) und wurde nicht intoniert.
Auszug: Brief Guidos an den Mönch Michael
In diesem Brief beschreibt Guido von Arezzo (992(ca.) - 1050) die pythagoreische Tonleiter folgendermaßen.
(Anschließend die authentischen und plagalen Kirchentöne).
(2) Die andern Töne, welche über diese sieben hinaus noch beigefügt werden, sind dieselben und klingen in jeder Beziehung ganz gleich, indem sie in Nichts eine Verschiedenheit zeigen, als nur darin, daß sie noch einmal so hoch tönen. Darum nennen wir auch die einen sieben die "tiefen", die andern sieben dagegen die "hohen".
Die sieben Buchstaben (zur Bezeichnung der Töne) werden aber nicht doppelt (d. h. einmal wie das andere Mal), sondern in verschiedener Weise so geschrieben:
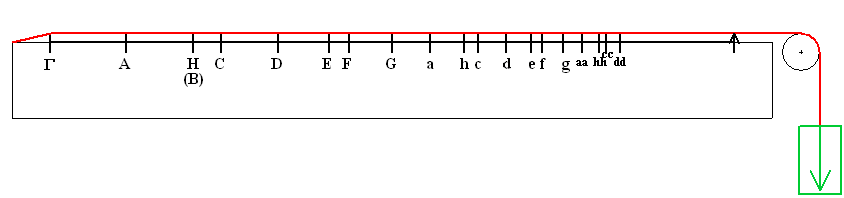
Gamma A B C D E F G a h c d e f g aa hh cc dd
Im Monochorde aber werden die Töne nach folgenden Buchstaben oder Maßen verteilt:
- Das griechische Gamma, im Lateinischen "G", setze an den Kopf. Von da anfangend teile die ganze Linie, welche unter der tönenden Saite liegt, ganz genau in neun Teile, und wo der erste Teil endet, da setze neben das Gamma als ersten Buchstaben den Buchstaben A.
- Von diesem ersten Buchstaben bis zum Endpunkte mache in gleicher Weise neun Teile, und wo der erste Teil endet, da füge als zweiten Buchstaben B [S..46b] hinzu.
- Hierauf gehe zum Buchstaben Gamma zurück, teile von diesem aus bis zum Ende in vier Teile, und setze am Endpunkte des ersten Teiles als dritten Buchstaben. C.
- In gleicher Weise mache von dem ersten Buchstaben A aus vier Teile, und zeichne ebenso als vierten Buchstaben D an.
- In derselben Weise, wie von dem ersten Buchstaben aus der vierte gefunden wurde, ebenso wird auch von dem zweiten aus als fünfter E,
- und von dem dritten aus als sechster F,
- und von dem vierten aus als siebenter G gefunden. Hierauf zurückgehend zum ersten Buchstaben A findest du in der Mitte von diesem bis zum Ende den andern ersten Buchstaben a, und in ähnlicher Weise vom zweiten aus den andern zweiten b, und vom dritten aus den andern dritten c; so auch von allen übrigen aus in gleicher Weise durch die ganze Reihe.
InFrequenzverhältnisse übersetzt bedeutet dies
- A:1G = Ganzton = 9:8 [1G: eine Oktave tiefer wie G]
- H:A = Ganzton = 9:8 [Im deutschen Sprachraum wird "H" statt "B" geschrieben.]
- c:1G = Quarte = 4:3
- D:A = Quarte = 4:3
- Man erhält nun die Tonfolge: G (Ganzton) A (Ganzton) H (Halbton) C (Ganzton) D
- Der Halbton hier als Differenz Quarte-2Ganztöne hat als Frequenzverhältnis 4:3/(9/8)^2 = 256/243, entspricht 90 Cent. Dieser pythagoreische Halbton wird auch "Leimma" genannt.
- Man erhält nun die Tonfolge: G (Ganzton) A (Ganzton) H (Halbton) C (Ganzton) D
- E:A = D:G = 3Ganztöne + Halbton = Ganzton + Quarte = Quinte = 3:2
- F:H = Quinte = 3:3
- G:1G = a:a = h:H = c:C = ... = Oktave = 2:1
Auf diese Weise erhält man die Tonfolge:
| A | H | C | D | E | F | G | a | ||||||
| Ganzton | Leimma | Ganzton | Ganzton | Halbton | Ganzton | Ganzton |
Das Quint-Terz-System
Der Intervallraum kaum wird von der Quinte Q, der großen Terz gT und der Oktave Ok erzeugt.I= {p·Q+q·gT+r·Ok| p,q,rεZ} = Z·Ok + Z·Q + Z·gt
(Jedes Intervall ist eindeutig als Linearkombination von Q, gT und Ok darstellbar).
Man erhält ein Tongeschlecht, die reine Stimmung, die sich am besten in der Eulerschreibweise erfassen lässt.
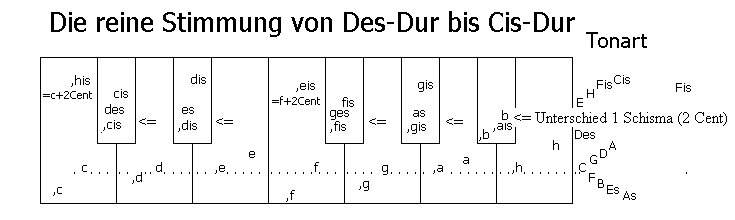
Weiter: Die reine Stimmung
