Joachim Mohr Mathematik Musik Delphi
Eine kurze Einführung finden Sie hier... und ein Größenvergleich der Intervalle hier ...
Viele Musikinstrumente und vor allem Sängerinnen und Sänger können feine Tonhöhennuancen von Intervallen abweichend von der gleichstufigen Stimmung realisieren. Sie können durch genaues Aufeinanderhören reine Oktaven, Quinten, Quarten, Terzen usw. verwirklichen. Je besser dies gelingt, umso besser ist der Klang. Dies beruht darauf, dass bei natürlichen Klängen neben dem Grundton auch Obertöne, deren Frequenz ein Vielfaches der Frequenz des Grundtons ist, mitschwingen. Fallen diese bei Akkorden teilweise zusammen, wird der Klang als harmonisch empfunden. Bei Verstimmungen wird der Klang rau.
Intervalltabelle der reinen Stimmung
Intervall Frequenzverhältnis Größe nach Mercator Syntonisches Komma ,e e 81:80 1k diatonischer Halbton ,e f 16:15 5k Kleiner Ganzton d ,e 10:9 8k Großer Ganzton c d 9:8 9k Kleine Terz c ’es 6:5 14k Große Terz c ,e 5:4 17k Quarte c f 4:3 22k Quinte c g 3:2 31k Kleine Sext c ’as 8:5 36k Große Sext c ,a 5:3 39k Kleine Septime g f 16:9 44k Kleine Septime ,a g 9:5 45k Große Septime c h 15:8 48k Oktave c c’ 2:1 53k
Die reine Stimmung
Folgende drei Vorkenntnisse sind erforderlich:
Vorkenntnisse auffrischen: Das pythagoreische und syntonische Komma
- Cent: Eine Oktave = 1200 Cent.
Mercator-Einteilung Übersichtlicher ist die Mercator-Einteilung 1 Oktave = 53k (siehe Tabelle oben) - Pythagoreisches Komma: Geht man 12 reine Quinten (Frequenzverhältnis 3/2) aufwärts und 7 Oktaven zurück, so ist der Unterschied zum Anfangston das pythagoreisches Komma (23,5 Cent). Deshalb sind unsere Klaviere heutzutage gleichstufig gestimmt. Hier sind die reinen Quinten im Quintenzirkel um 1/12 des pythagoreischen Kommas verkleinert und damit ist die Geschichte für viele Musiker zu Ende... Dabei hat diese Praxis eine lange Entwicklungszeit hinter sich. Mitteltönigen und wohltemperierten Stimmungen spielten jahrhunderte lang eine große Rolle.
- Syntonisches Komma: Geht man vier reine Quinten hoch - zum Beispiel c g d a e und zwei Oktaven zurück, so erhält man das Intervall c e, das sich von der reinen Terz c ,e (e mit "Tiefkomma" davor) um das syntonische Komma (21,5 Cent) unterscheidet.
Vorkenntnisse auffrischen: Das pythagoreische und syntonische Komma
Gioseffo Zarlino (1517-1590) bezeichnet die reine Stimmung als die "natürliche".
Dem Mathematike Leonhard Euler (1707–1783) verdanken wir die hier verwendete nützliche Schreibweise.
Dem Mathematike Leonhard Euler (1707–1783) verdanken wir die hier verwendete nützliche Schreibweise.
Alles, was Sie über die Eulerschreibweise wissen müssen.
Man geht vom Quintenzirkel mit reinen Quinten (Frequenzverhältnis 3/2) aus:
des as es b f c g d a e h fis cis (Alle Töne werden in derselben Oktavlage betrachtet).
Dann gilt folgende Schreibweise: Ein vorangestelltes "Tiefkomma", "Hochkomma" erniedrigt bzw. erhöht den Ton um ein syntonisches Komma.
In der additiven Schreibweise lautet die Dur- und Moll-Tonleiter:
die Zahlen in Klammer, den Abstand von c.
Die Größe eines Intervalls ist dann eindeutig bestimmt Zum Beispiel:
c-e = 18 Teile = 4 Quinten - 2 Oktaven = 409 Cent (≙ 81/64) pythagoreische große Terz
c-,e = 17 Teile = c-e - (synt.) Komma = 386 Cent (≙ 5/4) reine große Terz
c-es = 13 Teile = -3 Quinten + 2 Oktaven = 294 Cent (≙ 32/27) pythagoreische kleine Terz
c-'es = 14 Teile = c-es + (synt.) Komma = 316 Cent (≙ 6/5) reine kleine Terz
17 Teile = 1200*17/53 = 384,9 Cent - Reine Terz = 386,3 Cent
31 Teile = 1200*31/53 = 701,9 Cent - Reine Quinte = 702,0 Cent.
Man geht vom Quintenzirkel mit reinen Quinten (Frequenzverhältnis 3/2) aus:
des as es b f c g d a e h fis cis (Alle Töne werden in derselben Oktavlage betrachtet).
Dann gilt folgende Schreibweise: Ein vorangestelltes "Tiefkomma", "Hochkomma" erniedrigt bzw. erhöht den Ton um ein syntonisches Komma.
In der additiven Schreibweise lautet die Dur- und Moll-Tonleiter:
c(0) 9 d(9) 8 ,e(17) 5 f(22) 9 g(31) 8 ,a(39) 9 ,h(48) 5 c(53)
c(0) 9 d(9) 5 'es(14) 8 f(22) 9 g(31) 5 'as(36) 8 'b(44) 9 c(53)
Die tiefer gestellten Zahlen geben den Abstand zum Nachbarton an,die Zahlen in Klammer, den Abstand von c.
- Großer Ganzton = 9 Teile = 9/53 Oktave
- kleiner Ganzton = 8 Teile = 8/53 Oktave
- Halbton = 5 Teile = 5/53 Oktave
- Oktave = 53 Teile = 53/53 Oktave
Die Größe eines Intervalls ist dann eindeutig bestimmt Zum Beispiel:
c-e = 18 Teile = 4 Quinten - 2 Oktaven = 409 Cent (≙ 81/64) pythagoreische große Terz
c-,e = 17 Teile = c-e - (synt.) Komma = 386 Cent (≙ 5/4) reine große Terz
c-es = 13 Teile = -3 Quinten + 2 Oktaven = 294 Cent (≙ 32/27) pythagoreische kleine Terz
c-'es = 14 Teile = c-es + (synt.) Komma = 316 Cent (≙ 6/5) reine kleine Terz
Bemerkung
Die Abweichung dieser Teilung der Oktave in 53 Teile und der exakten Centwerte ist minimal. Zum Beispiel:17 Teile = 1200*17/53 = 384,9 Cent - Reine Terz = 386,3 Cent
31 Teile = 1200*31/53 = 701,9 Cent - Reine Quinte = 702,0 Cent.
Die reine C-Dur Tonleiter schreibt sich in der Eulerschen Schreibweise
c d ,e f g ,a ,h c. Hier haben die Dreiklänge
c-,e-g und f-,a-c sowie g-,h,d
reine große Terzen (Frequenzverhältnis 5/4), reine kleine Terzen (6/5) und reine Quinten (3/2).
Alle Durtonleitern schreiben sich nach dem selben Schema:
3. 6. und 7. Ton ein syntonisches Komma tiefer. Beispiele:
Der Molldreiklang c-es-g enthält die unreine große Terz es-g. Wenn wir das es um ein syntonisches Komma erhöhen, wird der Dreiklang rein. Für das erhöhte es schreiben wir 'es ("Hochkomma es"). Der Ton 'es erklingt also ein syntonisches Komma höher als der Ton es.
Alle Durtonleitern schreiben sich nach dem selben Schema:
3. 6. und 7. Ton ein syntonisches Komma tiefer. Beispiele:
Ton 1 2 ,3 4 5 ,6 ,7 8
...
D-Dur: d e ,fis g a ,h ,cis d
G-Dur: g a ,h c d ,e ,fis g
C-Dur: c d ,e f g ,a ,h c
F-Dur: f g ,a b c ,d ,e f
B-Dur: b c ,d es f ,g ,a b
...
Die reine C-moll Tonleiter (c-moll natürlich) schreibt sich dann
c d 'es f g 'as 'b c. Hier haben die Dreiklänge
c-'es-g und f-'as-c sowie g-'b-d
reine kleine Terzen (6/5), reine große Terzen (5/4) und reine Quinten (3/2).
Alle Molltonleitern schreiben sich nach dem selben Schema:
3. 6. und 7. Ton ein syntonisches Komma höher. Beispiele:
Im Quintenzirkel sind die einzelnen Töne folgendermaßen angeordnet.
Alle Molltonleitern schreiben sich nach dem selben Schema:
3. 6. und 7. Ton ein syntonisches Komma höher. Beispiele:
... Ton 1 2 '3 4 5 '6 '7 8 g-Moll: g a 'b c d 'es 'f g f-Moll: f g 'as b c 'des 'es f ... Die Paralleltonart und Gegentonart von C-Dur: ,a-Moll: ,a ,h c ,d ,e f g ,a ,e-Moll: ,e ,fis g ,a ,h c d ,e
Töne auf derselben vertikelen Linie (c und 'his oder des und ,cis usw.) unterscheiden sich nur um das Schisma.
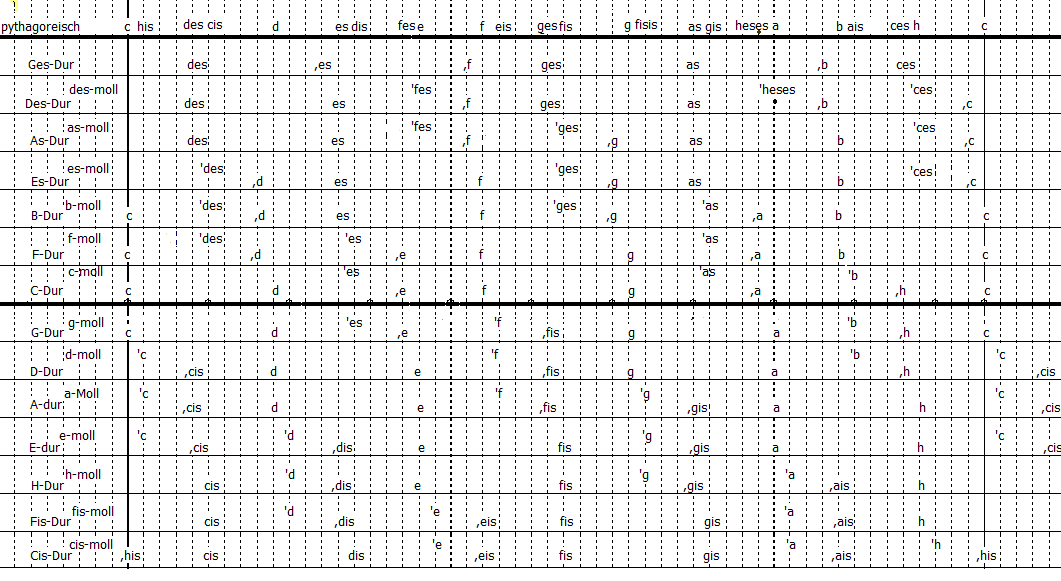
Die Vollkadenz in allen drei Lagen
In f-Dur: f g ,b c ,d ,e f (siehe unten "Modulationen")
rein
gleichstufig
Modulationen
Bekanntlich ändern sich bei Modulationen die Vorzeichen. In reiner Stimmung gibt es aber eine Besonderheit, die die Theorie kompliziert macht.Zur Einführung ein Klangbeispiel
c d ,e f g ,a ,h c. Hier sind folgende Terzen rein: c ,e / 'des f / d ',fis / 'es g / f ,a / g ,h / 'as c und 'b d rein erklingen.
Dann klingt es folgendermaßen:
Da die reine D-Dur-Tonleiter folgende Darstellung hat: d ,fis g a ,h ,cis d, muss man also 'des in ,cis und ,a in a umstimmen. Dann klingt es rein:
Faustregel: Bei einer Modulation in eine Nachbartonart ändern sich zwei Töne, einer davon erkennbar mit Vorzeichenwechsel, der andere geringfügig um ein syntonisches Komma mit der Größe von 22 Cent, etwa ein Fünftel Halbton.
Modulation in die Dominante
Vergleicht man dieC-Dur-Tonleiter c d ,e f g ,a ,h c mit der
G-Dur-Tonleiter g a ,h c d ,e ,fis g, so sieht man:
Das f hat sich mit Vorzeichenwechsel um einen Halbton zu ,fis erhöht, das ,a um ein syntonisches Komma zu a (im Notenbild unsichtbar) erhöht.
Beispiel: Dieselbe Melodie. Einmal in C-Dur, das andere Mal in G-Dur.
In C-Dur hat ,a die Frequenz von 440 Hz, in G-Dur hat a die Frequenz von 445,5 Hz. Diese Melodie bestimmt also schon - unter dem Gesichtspunkt der reinen Stimmung - die Tonart.
Die Melodie in C-Dur: h c ,e g ,a g
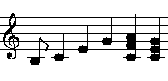
In G-Dur: h c ,e g a g
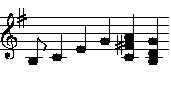
In G-Dur erklingt der Ton a höher als das ,a in C-Dur.
Spiele ,a in C-Dur (440 Hz) und a in G-Dur (445,5Hz) und beide und zusammen.
In C-Dur hat ,a die Frequenz von 440 Hz, in G-Dur hat a die Frequenz von 445,5 Hz. Diese Melodie bestimmt also schon - unter dem Gesichtspunkt der reinen Stimmung - die Tonart.
Die Melodie in C-Dur: h c ,e g ,a g
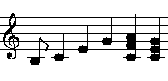
In G-Dur: h c ,e g a g
In G-Dur erklingt der Ton a höher als das ,a in C-Dur.
Spiele ,a in C-Dur (440 Hz) und a in G-Dur (445,5Hz) und beide und zusammen.
Modulation in die Subdominante
Vergleicht man dieC-Dur-Tonleiter c d ,e f g ,a ,h c mit der
F-Dur-Tonleiter f g ,a b c ,d ,e f, so sieht man:
Das h hat sich mit Vorzeichenwechsel um einen Halbton zu b erniedrigt, das d um ein syntonisches Komma zu ,d (im Notenbild unsichtbar) erniedrigt.
Modulation in den Tonikagegenklang
Vergleichen wir jetzt dieC-Dur-Tonleiter c d ,e f g ,a ,h c mit der
e-Moll-Tonleiter ,e fis g ,a ,h c d ,e.
Hier hat sich nur ein Ton geändert: das f zu fis erkennbar mit Vorzeichenwechsel um einen Halbton.
Modulation in die Tonikaparallele
Vergleichen wir nun dieC-Dur-Tonleiter c d ,e f g ,a ,h c mit der
a-Moll--Tonleiter ,a ,h c ,d ,e f g ,a.
Hier hat sich ebenfalls nur ein Ton geändert: das d hat sich um ein syntonisches Komma zu ,d erniedrigt.
Der Akkord auf der 2. Stufe in C-Dur ist deshalb mit ,d zu intonieren: ,d-f-,a. Sonst klingt der Akkord d-f-,a mit unreiner Terz d-f und unreiner Quinte d-,a.
Im Quintenzirkel kann man die Tonhöhen im folgendes Schema ablesen:
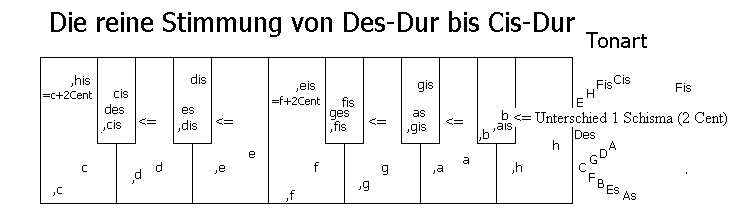
In dieser Darstellung sieht man die Lage der Töne im Quintenzirkel:
In der C-Dur-Reihe ... C-Dur: c d ,e f g ,a ,h c
Eine Zeile tiefer ist die Kommaveränderung zu F-Dur sichtbar: ,d statt d. F-Dur: f g ,a b c ,d ,e f
Darunter die Kommaveränderung zu B-Dur: ,g statt g. B-Dur: b c ,d es f ,g ,a b.
Darunter die Kommaveränderung zu Es-Dur: ,c statt c. Es-Dur: es f ,g as b ,c ,d es.
Darunter die Kommaveränderung zu As-Dur: ,f statt f. As-Dur: as b ,c des es ,f ,g as.
Über der C-Dur-Tonleiter die Kommaveränderung zu G-Dur: a statt ,a. G-Dur: g a ,h c d ,e ,fis g .
Darüber die Kommaveränderung zu D-Dur: e statt ,e. D-Dur. d e ,fis g a ,h ,cis d.
Darüber die Kommaveränderung zu A-Dur: h statt ,h. A-Dur. a h ,cis d e ,fis ,gis a.
Die weiteren Kommaveränderungen erscheinen bei den "schwarzen" Tasten:
Nach As-Dur die Kommaveränderung zu Des-Dur:,b statt b. Des-Dur des es ,f ges as ,b ,c des.
Nach A-Dur die Kommaveränderung zu E-Dur: fis statt ,fis. E-Dur: e fis ,gis a h ,cis ,dis e.
Darüber Kommaveränderung zu H-Dur: cis statt ,cis. H-Dur: h cis ,dis e fis ,gis ,ais h.
Darüber Kommaveränderung zu Fis-Dur: gis statt ,gis. Fis-Dur: fis gis ,ais h cis ,dis ,eis fis.
Darüber Kommaveränderung zu Cis-Dur: dis statt ,dis. Cis-Dur: cis dis ,eis fis gis ,ais ,his cis.
Töne, die sich nur um ein Schisma (2 Cent) unterscheiden, kann man in der Praxis gleichsetzten.
,his=c+2Cent / ,cis=des+2Cent / ,dis=es+2Cent / ,eis=f+2Cent /,fis=ges+2Cent / ,gis=as+2Cent / ,ais=b+2Cent
Ob die Intervalle rein oder unrein erklingen, erkennt man an ihrer Darstellung. Reine große Terzen sind von der Form x-,y, zum Beispiel: b-,d, des-,f oder cis-,eis.
Intervallberechnungen sind in dieser Darstellung einfach. Beispiel: as und gis unterscheiden sich um das pythagoreische Komma. Da ,gis ein syntonisches Komma tiefer als gis erklingt, hat das Intervall ,gis as eine vernachlässigbare Größe. nämlich:
Schisma = pythagoreisches Komma - syntonisches Komma = 2 Cent.