Die Homepage von Joachim Mohr
In der Eulerschreibweise ist der Ton ,his (Tiefkomma his) ein synt. Komma tiefer wie der Ton his.
Das vom Hören her vernachlässigbare Schisma spielt in der Theorie der wohltemperierten Stimmung oder des Reinharmoniums (oder Archicembo usw.) eine große Rolle.Nach 12 Quinten erhält man oktaviert von c aus den Ton his, der ein pythagoreisches Komma höher als c ist. In den Tonleitern des Quintenzirkels erscheint jedoch zum Beispiel bei Cis-Dur der Ton ,his, der ein syntonisches Komma tiefer ist als his, ist und sich von c nur um ein Schisma unterscheidet.
Dieser minimale Unterschied kann bei wohltemperierten Stimmungen oder dem Reinharmonium vernachlässigt werden. Werckeister schreibt, dass dieses Intervall auf dem Monochord "kaum einen Circulstrich" ausmacht (Zitiert nach W. Neumaier S.227).
Schisma
Definition: Das Schisma (Größe: rund 2 Cent) ist die Differenz des pythagoreischen Kommas und des syntonischen Kommas.
Schisma = pythagoreisches Komma - syntonisches Komma = 23,46 - 21,51 Cent = 1,95 Cent.
Berechnung des Frequenzverhältnisses:
pythaoreisches Komma = 12 Quinten - 7 Oktaven:
3 12 7 531441
Frequenzverhältnis des pythagoreischen Kommas: (-) : 2 = ——————.
2 524288
syntonisches Komma = pythag. große Terz - reine große Terz = (4 Quinten - 2 Oktaven) - reine gr. Terz
3 4 2 5 81
Frequenzverhältnis des syntonischen Kommas: (-) : 2 : - = ——.
2 4 80
531441 81 32805
Frequenzverhältnis des Schismas: —————— : —— = —————.
524288 80 32768
Frequenzverhältnis des Schismas: 32805/32768=1.001129150390625.
Wo spielt dieses Intervall eine Rolle
I) Siehe: Hermman von Helmholz unten den Abschnitt Das Reinharmonieum.
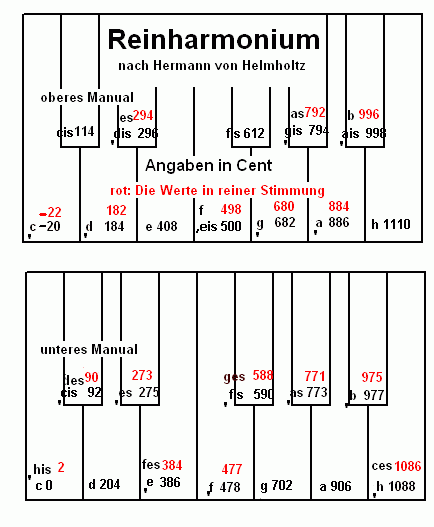
Zu allen rot eingezeichneten Centangaben gibt es einen Ton, der sich nur um ein Schisma unterscheidet.
II) Und siehe Eulerschreibweise unten den Abschnitt Für historisch interessierte Musiker.
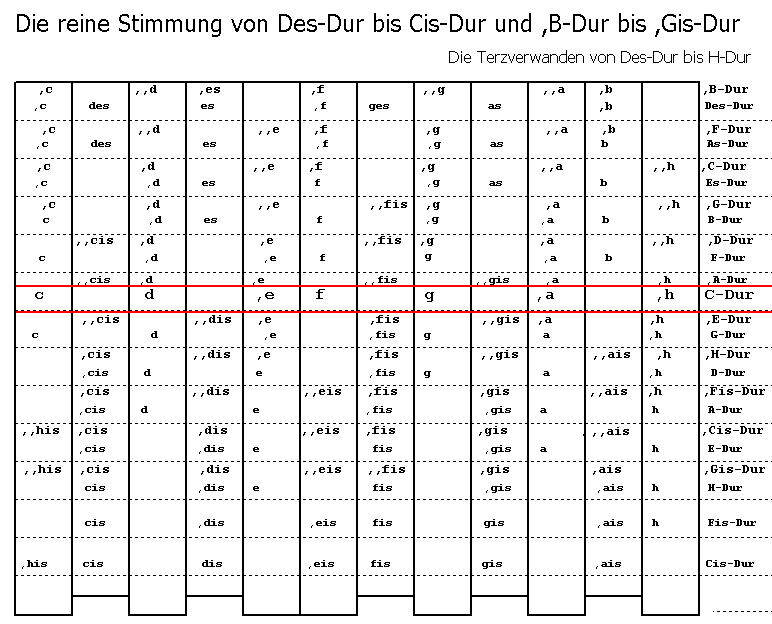
Wenn man versucht, die 12-stufige Tastatur durch weiter Tasten zu erweitern, damit man im Quintenzirkel alle Tonarten von zum Beispiel von Dis-Dur nach Ces-Dur und die dazu Terzverwanden Tonarten von ,B-Dur bis ,Cis-Dur, so kann man Tasten einsparen, wenn man Töne, die sich nur um ein Schisma unterscheiden identifiziert (Den Unterschied kann das menschliche Gehör nicht hören.)
Dann ist ,his=c / ,cis=des / ,,dis=,es / ,dis=es / ,,e=,f / ,e=f / ,fis=ges / ,gis=as / ,,ais=,b und ,ais=b. H-Taste: 3
III) Und siehe: Die reine Stimmung
In alten Singschulen konnte man mit den theoretischen Verhältnissen der Intervalle wenig anfangen. Seit Guido von Arrezzo (992 bis 1050) kannte man die arithmetische Einteilung. Hier hatte man eine gute Vorstellung der Größen der Intervalle.
Großer Ganzton (c-d) = 9 Teile
Kleiner Ganzton (d-,e) = 8 Teile
Diatonischer Halbton (,e-f) = 5 Teile
Chromatischer Halbton ('b-h oder f-,fis) = 4 Teile
Große Terz (c-,e) = 17 Teile
Quinte (c-g) = 31 Teile
Oktave (c-c') = 53 Teile
Dies stellt die Größenverhältnisse in hervorragender Weise dar. Der Fehler zum exakten Wert liegt in der Größenordnung von einem Schisma (2 Cent).
Die Abstände der Töne der C-Dur-Tonleiter sind den alten Singschulen wohlbekannt:
Großer Ganzton (c-d) = 9 Teile
Kleiner Ganzton (d-,e) = 8 Teile
Diatonischer Halbton (,e-f) = 5 Teile
Chromatischer Halbton ('b-h oder f-,fis) = 4 Teile
Große Terz (c-,e) = 17 Teile
Quinte (c-g) = 31 Teile
Oktave (c-c') = 53 Teile
Dies stellt die Größenverhältnisse in hervorragender Weise dar. Der Fehler zum exakten Wert liegt in der Größenordnung von einem Schisma (2 Cent).
Die Abstände der Töne der C-Dur-Tonleiter sind den alten Singschulen wohlbekannt:
c d ,e f g ,a ,h c 9 8 5 9 8 9 5Die Oktave hat dann nach Mercator den Abstand von 53 Teilen.
Weiterlesen: Die additive Größe von Intervallen.
