Joachim Mohr   Mathematik Musik
≡
Lektion 1   Lektion 2    Lektion 3  Lektion 4   Lektion 5   Lektion 6   Lektion 7   Lektion 8   Lektion 9

6. Lektion: Das pythagoreische
und
syntonische Komma

Jetzt, wo in der Überschrift das Stichwort gefallen ist, wird eine historische Bemerkung fällig.

Pythagoras von Samos (5. Jh. v. Chr.) war der Auffassung: "Alles ist Zahl" und dies bestätigte sich in der Musiktheorie aufs beste. Pythagoras experimentierte auf dem Monochord, bei dem über einem quaderförmigen Resonanzkörper eine Saite gespannt ist, die an einem Ende fest verankert und am anderen Ende über eine feste Rolle mit einem Gewicht belastet ist, dadurch also immer die gleiche Spannung hat. Mit einem beweglichen Steg konnte er die Saitenlänge verändern. Ganz im Sinne der Experimentalphysik, die eigentlich erst mit Galileo Galilei (1564-1642) begann, untersuchte Pythagoras die Tonhöhe in Abhängigkeit von der Saitenlänge und fand dabei heraus - wie Euklid 300 vor Christus in seiner Schrift "Teilung des Kanons" erläutert:
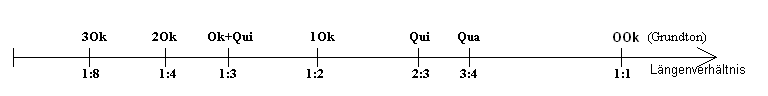
oktavreihe_pyth.gif
Seine Vehältniszahlen sind die Kehrwerte der Frequenzverhältnisse. Um die Lektionen einheitlich zu gestalten, nehmen wir uns die Freiheit und drehen die Verhältnisse um.
Der Quart entspricht das Verhältnis 4:3
Der Quint entspricht das Verhältnis 3:2
Der Oktav entspricht das Verhältnis 2:1
Der Quint+Oktave entspricht das Verhältnis 3:1
Der Doppeloktave entspricht das Verhältnis 4:1
Des Weiteren fand er heraus, dass dem Nacheinanderausführen zweier Tonschritte die Multiplikation der entsprechenden Verhältniszahlen entspricht. Er konnte also Berechnungen über Intervalle - wie wir mit Hilfe der Akustik - mit Hilfe der Verhältniszahlen durchführen.

So folgerte er: Dem Ganzton als Differenz von Quint und Quart entspricht das Verhältnis 9:8.

Und: Die Oktave ist kleiner als 6 Ganztöne. Den Unterschied zwischen Oktav und 6 Ganztönen nennen wir das pythagoreische Komma.

Da für den Ganzton gilt: G =2·Qui - Ok ist Ok 〈 6G gleichbedeutend Ok〈12Qui-6Ok oder 7Ok〈12Qui. In dieser Weise wird das pythagoreische Komma meist erläutert.

Das pythagoreische Komma

Geht man von c 12 Quinten nach oben und 7 Oktaven zurück, so landet man bei einem Tasteninstrument auf dem selben Ton c. In Wahrheit handelt es sich jedoch um His.

Die 12 Töne der Quintenfolgen sind:

c g d' a' e'' h'' fis''' cis'''' gis'''' dis''''' ais''''' eis'''''' his''''''

7 Oktaven zurück:

his'''''' his''''' his'''' his''' his'' his' his His

Der Unterschied zwischen His und c wird als pythagoreisches Komma bezeichnet. Genauer:

pythagoreische Komma = 12Qui - 7Ok

Das Frequenzverhältnis ist 
     3 12   7   531441
q = (-)  : 2  = —————— = 1,013 643 265
     2          524288
oder - und hier sieht man den Vorteil der Centangabe - pythagoreische Komma = 1200*lb(q) = 23,46 Cent, ungefähr ein Fünftel Halbton (h = 100 Cent).

pythagoreische Komma= 23,5 Cent

Historische Bemerkung: Von Aristoxenos (2. Hälfte des 4.Jh. v. Chr.), ein scharfer Logiker, ist die früheste Tonsystemtheorie mit dem Titel "Harmonische Elemente" in Fragmenten überliefert (siehe Literatur: Neumaier). Aristoxenos argumentierte rein hörpsychologisch, er verwendete keine Verhältnisse. Er stellte durch Hören fest, dass die Quarte zweieinhalb Ganztöne beträgt (was nur fast stimmt) und konnte damit logische eine in sich stimmige Theorie aufbauen. Euklid deckt den Fehler auf: "Die Quarte ist kleiner als zweieinhalb Ganztöne".

Genauer: Aristoxenos machte einen Hörtest und behauptete: Qua - 2G + Qua - 2G + Qua sei eine Quinte = Quarte + Ganzton und folgerte aus 3Qua - 4 G = Qua + G, dass 2Qua = 5G, also Qua = 2 1/2G. 
                                4        9
Rechnen wir nach: 3Qua-4G = 3lb(-) - 4lb(-) = 678,495 Cent
                                3        8
Der Vergleich mit der Quinte Qui = 701,955 Cent ergibt als Differenz 23,46 Cent. Aristoxenos "verhörte" sich exakt um das pythagoreische Komma.
Eine Bemerkung zu His = c (angeblich): Das His wie oben durch 12 Quinten - 7 Oktaven bestimmt, kommt normalerweise so in Modulationen gar nicht vor, es sei denn, man stimmt sein Instrument nur mit reinen Quinten. Dann ist der Unterschied zwischen c und His tatsächlich das pythagoreische Komma.

Wir begeben uns nun aber in die Betrachtungsweise der reinen Stimmung.

Schon in der Quintenreihe c g d' a' (alles reine Quinten) ist dieses a' kein a der C-Dur-Tonleiter mehr, da das Intervall ga' in C-Dur ein kleiner Ganzton ist. Nur in G-Dur ist g'a' ein großer Ganzton.

Suchen wir ein passendes His! Zum Beispiel bei der Modulation C-Dur über E-Dur nach cis-moll.

Cis-moll hat noch das ,e von C-Dur. Von c = 0 Cent aus gerechnet: ,e = 386,314 Cent (Im Eulerschen Tonnetz: ,e [Tiefkomma e]). Eine kleine Terz (gT = 315,641 Cent) tiefer ergibt: Cis = 70,672 Cent (Im Eulerschen Tonnetz ,,Cis). His wäre ein Halbton tiefer: His = - 41,059 Cent (Im Eulerschen Tonnetz: ,,,His). Das ist fast ein halber Halbton zu tief im Vergleich zu c! Diese Differenz besteht auch zwischen Cis und Des.
Eine Bemerkung zur pythagoreischen Tonleiter: Bis in die Renaissance ist von Tetrachorden, Tongeschlechtern bzw. Kirchentönen die Rede. Unter diesen Betrachtungen kann man eine Aufeinanderfolge von Tönen als die diatonische (=Dur-)Tonleiter finden.

Erst mit der Mehrstimmigkeit erkannte man, dass die große Terz (386 Cent) viel wohlklingender ist als der Ditonos (Ditonos = 2 große Ganztöne = 408 Cent). In der folgenden Tonleiter kommt die große Terz nicht vor.
Die pythagoreischen Tonleiter hat folgende Intervalle zum Grundton:

G, 2G, Qua, Qui, Qui+G, Qui+2G und Ok. Übersetzt in die C-Dur-Tonleiter erhalten wir im Vergleich:

  c d e f g a h c'  
rein 0 204 386 498 702 884 1088 1200 Cent
pythagoreisch 0 204 408 498 702 906 1110 1200 Cent
gleichstufig 0 200 400 500 700 900 1100 1200 Cent


Fachleute bestätigen den Wohlklang dieser Tonschritte beim einstimmigen Singen.

In der pythagoreischen Stimmung fällt auf:

Die "große Terz" ce, genauer der Ditonos ist "geschärft" (um 22 Cent größer als die reine Terz).
Der "Halbton" ef bzw. hc, genauer das Leimma ist "eng" (um 22 Cent kleiner als der reine Halbton).
Sie hat Ähnlichkeiten mit der gleichstufigen Stimmung.

Zum Nachschlagen:
Intervall Frequenzverhältnis in Cent
reine große Terz = G + (G-) 4:3 386
Ditonos = 2G 81:64 408
reiner Halbton 16:15 112
Leimma = Quart - 2G 256:243 90

Das syntonische Komma (Terzkomma)

Unter dem syntonischen Komma, auch Terzkomma genannt, versteht man die Differenz zwischen 2 großen Ganztönen und der großen Terz.

Anders ausgedrückt ist das syntonische Komma der Unterschied zwischen Ditonos und großer Terz.

K = syntonisches Komma = 2G - gT

Das ist genau der Unterschied zwischen dem großen Ganzton und dem kleinem Ganzton.

K = G - (G-) oder G- = G - K 

                                      9 9 5   81
Berechnung des Frequenzverhältnisses: -·-:- = ——
                                      8 8 4   80
In Cent: 2·lb(9/8) - lb(5/4) = lb(81/80) = 21,5 Cent

K = 21,5 Cent

Mit Aufkommen der Mehrstimmigkeit erkannte man allmählich den Wohlklang der reinen Terz. Der Ditonos dagegen wurde als Dissonanz vermieden. Und nun begann ein Umschwung:

In der Durtonleiter lies man den dritten Ton zum Grundton als reine Terz erklingen. Dieser dritte Ton, und ähnlich der 6. und 7. Ton, musste deshalb im Vergleich zur pythagoreischen Tonleiter gerade um das syntonische erniedrigt werden.

Diese Stimmung (siehe oben) heißt die reine Stimmung.

Die Tonleiter der reinen Stimmung ist so gestimmt dass bei der Kadenz mit Tonika, Dominante und Subdominante ( in C-dur die Akkorde ceg, afc und ghd) rein erklingen, d.h. nur reine Quinten, große und kleine Terzen vorkommen.

Da der 3., der 6. und der 7. Ton der Tonleiter um das syntonische Komma erniedrigt werden müssen (im Vergleich zur pytagoreischen Tonleiter), wird von Theoretikern häufig die reine C-Dur-Tonleiter folgendermaßen geschrieben:

c d e f g a h c' (der 3., 6. und 7. Ton unterstrichen).

Wir verwenden die typographisch einfachere Schreibweise: c d ,e f g ,a ,h c

Damit wird angedeutet, dass cg und fc' sowie gd' reine Quinten und c,e und f,a sowie g,h reine große Terzen sind. In der Quintenfolge "f c g d a e h" muss also e, a und h um ein syntonisches Komma erniedrigt werden, was durch das Tiefkomma angedeutet werden soll.

Weitere Mikrointervalle

In der historischen Literatur werden noch folgende "Kleine" Intervalle genannt (in Klammer Frequenzverhältnisse):
großes Chroma (135/128) = großer Ganzton (9/8) - diatonischem Halbton (16/15) = 91,18 Cent
kleines Chroma (25/24) = kleiner Ganzton (10/9) - diatonischem Halbton (16/15) = 70,67 Cent
(Chroma = chromatischer Halbton)
Diaschisma (2048/2025) = diatonischer Halbton (16/15) - große Chroma (135/128) = 19,55 Cent
Schisma (32805/32768) = pythagoreisches Komma (531441/524288) - syntonisches Komma (81/80) = 1,95 Cent
kleine Diesis (128/125) = Oktave (2) - drei große Terzen ((5/4)3) = 41,06 Cent
große Diesis (648/625) = vier kleine Terzen ((6/5)4) - Oktav (2) = 62,57 Cent

Limma (256/243) = Quarte (4/3) - pythagoreische Terz (81/64) = 90,22 Cent
Apotome (2187/2048) = pythagoreische übermäßige Prim (C-Cis) = sieben Quinten ((3/2)7) - 4 Oktaven (16) = 113,69 Cent
Siehe auch die Intervalltabelle

Weiter mit ...