Joachim Mohr Mathematik Musik Delphi
Zurück
Gruppen
(G,⋅) heißt Gruppe, wenn für die Verknüfung ⋅ gilt:- ⋅ ist assoziativ: a⋅(b⋅c)=a⋅(b⋅c)
- Es gibt ein neutrales Element e: Für alle x∈G gilt: x⋅e=e⋅x=x
- Zu jedem Element x∈G gibt es ein Inverses y∈G mit x⋅y=y⋅x=e
Beweis: Seine y und z invers zu x. Dann gilt:
z⋅(x⋅y)=z⋅e=z und (z⋅x)⋅y=e⋅y=y, also z=y. ✅
Das Inverse von x wird hier mit x-1 bezeichnet: x-1⋅x=x⋅x-1=e.
Lemma: (x-1)-1=x
Beweis: x=e⋅x=((x-1)-1⋅x-1)⋅x=(x-1)-1⋅(x-1x) =(x-1)-1⋅e=(x-1)-1 ✅
Lemma: (a⋅b)-1=b-1⋅a-1.
Beweis: (a⋅b)⋅b-1⋅a-1=e ✅
Lemma: Aus a⋅b=a⋅c folgt: b=c. Beweis: multipliziere links a-1. ✅
Beispiele für Gruppen
Bekannt
(ℤ,+) die additive Gruppe der ganzen Zahlen.(ℚ,+) die additive Grruppe der rationalen Zahlen ℚ.
(ℚ\{0},·), die multiplikative Gruppe der rationalen Zahlen ohne die 0.
Analog (ℝ,+) und (ℝ\{0}, ⋅) die reellen Zahlen.
Gruppe mit 1 Element
Es gibt -bis auf Isomorphie- nur eine Gruppe mit einem Element: die triviale Gruppe G={e}.Gruppe mit 2 Elementen
Es gibt -bis auf Isomorphie- nur eine Gruppe G={e,a} mit zwei Elemenenten, wobei aa=e.Diese Gruppe kann auch geschrieben werden als G={1,-1}, wobei (-1)(-1)=1.
⋅ | 1 -1 ———————— 1| 1 -1 -1|-1 1
Gruppe mit 3 Elementen
(FLAN 19) Es gibt -bis auf Isomorphie- nur eine Gruppe mit 3 Elementen, die zyklische Gruppe {e,a,a2}.Mit b=a2 erhält man die Gruppentafel
⋅ | e a b —————————— e| e a b a| a b e b| b e a
Gruppen mit 4 Elementen
Es gibt -bis auf Isomorphie- nur zwei Gruppen mit 4 Elementen.- Die zklische Gruppe. Additiv geschrieben G={0,1,2,3}=ℤ4 mt 1+1=2 und 1+1+1=3 oder
multiplikativ geschrieben G={e, a, b,c} mit b=a2 und c=a3.+ | 0 1 2 3 * | 1 a b c ——————————— ——————————— 0 | 0 1 2 3 1 | 1 a b c 1 | 1 2 3 0 a | a b c 1 2 | 2 3 0 1 b | b c 1 a 3 | 3 0 1 2 c | c 1 a b
- Die Kleinsche Vierergruppe (1884 Vorlesungen über das Ikosaeder).
Die Kleinsche Vierergruppe ist die alternierende Gruppe A4 (s.u.) von S4.
Als Elemente von S4 betrachtet ist a=(1→2)(3→4) b=(1→3)(2→4) ab=(1→4)(2→3) Die Kleinsche Vierergruppe ist isomorph zu ℤ2×ℤ2 (Beachte in ℤ2: 1+1=0).⋅ | e a b ab + | (0,0) (1,0) (0,1) (1,1) ———————————————— ————————————————————————————————— e | e a b ab (0,0) | (0,0) (1,0) (0,1) (1,1) a | a e ab b (1,0) | (1,0) (0,0) (1,1) (0,1) b | b ab e a (0,1) | (0,1) (1,1) (0,0) (1,0) ab| ab b a e (1,1) | (1,1) (0,1) (1,0) (0,0)
FLA 15
Das 5-Eck in der komplexen Zahlenbene als Gruppe
Pentagramm
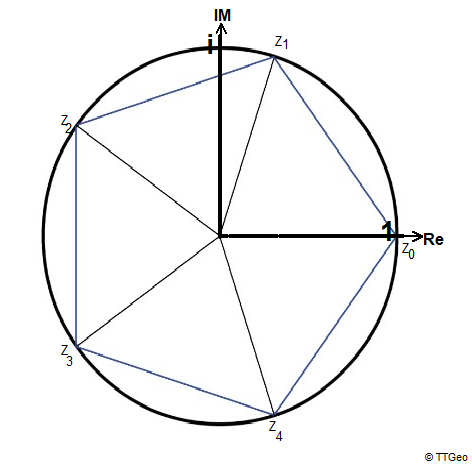
0·2π·i
z0=exp(——————)=1
5
1·2π·i
z1=exp(——————)=cos(72°)+i·sin(72°)
5
2·2π·i
z2=exp(——————)=cos(144°)+i·sin(144°)
5
3·2π·i
z3=exp(——————)=cos(216°)+i·sin(216°)
5
4·2π·i
z4=exp(——————)=cos(288°)+i·sin(288°)
5
Die Multiplikation mit den Einheitswurzeln ergeben die Drehungen des Pentagramms:
id=um 0°, z1 um 72°,z2 um 144°, z3 um 216° und z4 um 288°.
Gruppentafel:
· |id|z |z |z |z |
| | 1| 2| 3| 4|
——————————————————
id|id|z |z |z |z |
| | 1| 2| 3| 4|
——————————————————
z |z |z |z |z |id|
1| 1| 2| 3| 4| |
——————————————————
z |z |z |z |id|z |
2| 2| 3| 4| | 1|
——————————————————
z |z |z |id|z |z |
3| 3| 4| | 1| 2|
——————————————————
z |z |id|z |z |z |
4| 4| | 1| 2| 3|
——————————————————
Die Gruppe {id, z1, z2, z3, z4,·} ist isomorph zu (ℤ5,+).
Permutationsgruppen
Eine Permutation ist eine bjektive Abbildung von M={1,2,3,...,n} auf M. (M kann auch eine beliebige Menge sein).Eine Gruppe G von Permutationen ist zum Beispiel die Symmetriegruppe eines Würfels mit den Ecken M={1,2,3,4,5,6,7,8}.
Beispiele aus S5.
Statt σ(1)=3, σ(2)=2, σ(3)=4, σ(4)=1 und σ(5)=5 schreibt man: 1 2 3 4 5 σ=( ). Als Zyklus geschrieben Zyklus σ=(1→3→4) (damit auch 4→1) 3 2 4 1 5
In der Literatur findet man auch folgende Schreibweise:
σ=(3 2 4 1 5) Als Zyklus geschrieben Zyklus σ=(1,3,4)
Multiplikation στ "σ nach τ": Zuerst τ, dann σ.
σ=(3 2 4 1 5) Als Zyklus geschrieben Zyklus σ=(1,3,4)
1 2 3 4 5 1 2 3 4 5
Für σ=( ) und τ=( ) ist dann das Produkt "σ nach τ":
3 2 4 1 5 5 3 2 1 4
1 2 3 4 5 1 2 3 4 5
στ = ( ) und "τ nach σ" τσ=( )
5 4 2 3 1 2 3 1 5 4
Ein Zyklus (a→b), der nur zwei Elemente vertauscht, heißt Transposition.
Jede Permutation σ lässt sich als Produkt von n-Transpositionen schreiben.
Ist n gerade, ist das Signum sign(σ)=+1, sonst sign(σ)=-1.
1 2 3 4 5 1 2 3 4 5
Beispiel: (1→2→5)=(1→2)(2→5)=( ) (2→5)(1→2) = ( ) =(1→5→2)
2 5 3 4 1 5 1 3 4 2
Alle "geraden" Permutuationen von Sn, also die Permutationen σ mit sign(σ)=1, bilden eine Untergruppe, die alternierende Gruppe An.
Die Permutationsgruppe S3
Genannt auch die symmetrische Gruppe S3 aller Permutationen der Menge {1,2,3} .Die Permutationen hier sind die bijektiven Abbildungen f von M auf M.
Die Bezeichnung f=(a,b,c) bedeutet: f(1)=a f(2)=b f(3)=c.
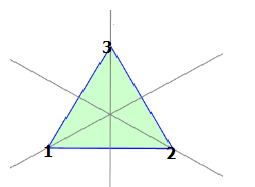
S3 kann gesehen werden
als die Symmetriegruppe
des gleichseitigen Dreiecks
mit drei Drehungen d0, d1, d2
und den drei Spiegelungen s1, s2, s3
Identität = Drehung d0 um 0°. s0=(1 2 3).
Drehung um 120°. d1=(2 3 1)=(1→2→3)
Drehung um 240°. d2=d1⋅d1=(3 1 2)=(1→3→2)
Spiegelung, die Punkt 1 festläßt: s1=(1 3 2)=(2→3)
Spiegelung, die Punkt 2 festläßt: s2=(3 2 1)=(1→3)
Spiegelung, die Punkt 3 festläßt: s3=(2 1 3)=(1→2)
Beispiel für die Berechnung von d1⋅s1=(2 1 3)=s2.
Gruppentafel
⋅ | d0 d1 d2 s1 s2 s3 invers ———————————————————————— —————— d0 | d0 d1 d2 s1 s2 s3 d0 d1 | d1 d2 d0 s2 s1 s3 d2 d2 | d2 d0 d1 s1 s3 s2 d1 s1 | s1 s2 s3 d0 d1 d2 s1 s2 | s2 s3 s1 d2 d0 d1 s2 s3 | s3 s1 s2 d1 d2 d0 s3Das neutrale Element ist d0: a⋅d0=a für alle d∈S3.
S3 ist nicht kommutativ. Beispiel: s2⋅d1≠d1⋅s2 (s3≠s1)
Gruppentafel in Zyklenschreibweise
⋅ |id (1→2→3) (1→3→2) (2→3) (1→3) (1→2) invers ————————————————————————————————————————————————————— ——————— id |id (1→2→3) (1→3→2) (2→3) (1→3) (1→2) id (1→2→3)|(1→2→3) (1→3→2) id (1→3) (2→3) (1→2) (1→3→2) (1→3→2)|(1→3→2) id (1→2→3) (2→3) (1→2) (1→3) (1→2→3) (2→3) |(2→3) (1→3) (1→2) id (1→2→3) (1→3→2) (2→3) (1→3) |(1→3) (1→2) (2→3) (1→3→2) id (1→2→3) (1→3) (1→2) |(1→2) (2→3) (1→3) (1→2→3) (1→3→2) id (1→2)
Multiplikationstabelle für Z modulo 11
(ℤ11\{0},*) ist abelsche Gruppe.| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 1 | 3 | 5 | 7 | 9 |
| 3 | 3 | 6 | 9 | 1 | 4 | 7 | 10 | 2 | 5 | 8 |
| 4 | 4 | 8 | 1 | 5 | 9 | 2 | 6 | 10 | 3 | 7 |
| 5 | 5 | 10 | 4 | 9 | 3 | 8 | 2 | 7 | 1 | 6 |
| 6 | 6 | 1 | 7 | 2 | 8 | 3 | 9 | 4 | 10 | 5 |
| 7 | 7 | 3 | 10 | 6 | 2 | 9 | 5 | 1 | 8 | 4 |
| 8 | 8 | 5 | 2 | 10 | 7 | 4 | 1 | 9 | 6 | 3 |
| 9 | 9 | 7 | 5 | 3 | 1 | 10 | 8 | 6 | 4 | 2 |
| 10 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Inverses | 1 | 6 | 4 | 3 | 9 | 2 | 8 | 7 | 5 | 10 |
Untergruppen
Sei G Gruppe und H⊂G. H heißt Untergruppe, wenn H selbst Gruppe ist, wenn also gilt:- a,b∈H ⇒ ab∈H und
- II a∈H ⇒ a-1 ∈H.
Sei G endlich und |G| die Anzahle der Elemente von G. Dann gilt:
|H| ist ein Teiler von G.
Beweis: Wir betrachten die Linken Nebenklassen aH (a∈G) von H.
Für a,b∈G gilt aH=bH oder aH∩bH=∅ (leere Menge).
|aH|=|H| für a∈G
Es gibt also a1,a2,...am∈G so, dass alle Mengen ai und aj für i≠j disjunkt sind.
G=a1H+a2H+...+amH ⇒|G|=m|H| ✅
Folgerung |G|=|H|·|G/H| für G/H={aH|a∈G} mit aH·bH=ab·H.
Kommutatoren
Beispiel:
1 2 3 4 5 -1 1 2 3 4 5 1 2 3 4 5 -1 1 2 3 4 5
a=( ) a = ( ) b=( ) b = ( )
3 4 5 2 1 5 4 1 2 3 5 4 2 1 3 4 3 5 2 1
-1 -1 1 2 3 4 5
Kommutator a·b·a· b = ( ) =(1→2)(3→4) sign = +1 (immer!)
2 1 4 3 5
1 2 3 4 5 -1 1 2 3 4 5 1 2 3 4 5 -1 1 2 3 4 5
σ=( ) σ = ( ) τ=( ) τ = ( )
3 1 5 2 4 2 4 1 5 3 1 5 4 2 3 1 4 5 3 2
-1 -1 1 2 3 4 5
Kommutator σ·τ·σ ·τ = ( )=(1→4→3→2→5)=(1→4)(4→3)(3→2)(2→5)
4 5 2 3 1
A4
A4 ist die Kommutatorgruppe von S4. Oder:A4 enhält alle Elemente von S4 mit Signum=+1 (gerade Permutationen).
-1 -1
A =<{aba b |a,b∈S }>. S hat 24 Elemente, A hat 12 Elemente.
4 4 4 4
(Die Klammer <...> bedeutet: "wird erzeugt.")
Permutationen werden hier als Zyklen beschrieben.
1234 1234 1 2 3 4
Beispiel: (2→3)(1→3→4)=( )*( ) = ( ) = (1→2→3→4)
1324 3241 2 3 4 1
A4 wird erzeugt von: a=(1→2)(3→4) und b=(1→2→3).
2 -1
a =id ⇒ a = a
2 3 -1
bb=b = (1→3→2) b =id ⇒ b =bb
ab=a*b=(2→4→3) ba=b*a=(1→3→4)
abb=a*bb=(1→4→3)=baba bba=(2→3→4)
aba=(1→4→2) baa=b bab=(1→2→4)=abab
abab=bba babb=(1→4)(2→3) abba=(1→2→4) ababb=(1→4)(2→3)
A4 besteht aus dem Produkt von drei Zweierzyklen a, babb und ababb
sowie den Dreierzyklen b, bb, ab, ba, abb, bba, aba, bab und abba.
Die Kleinsche Vierergruppe (s.o.) ist die Kommutatorgruppe von A4.
Zyklische Gruppen
Definition: Eine Gruppe G ist zyklische, wenn sie von einem einzigen Element a∈G erzeugt wird, d.h.
Die Gruppe (G,·) ist zyklich wenn es ein a∈G gibt (das erzeugende Element) so, dass G={an|n∈ℤ}.
Die Gruppe (G,+) ist zyklich wenn es ein a∈G gibt (das erzeugende Element) so, dass G={n·a|n∈ℤ}, wobei n·a=a+a+...+a (n mal).
Satz: Ist |G| (=Anzahl der Elemente von G) eine Primzahl p, so ist G zyklisch.
Die Gruppe (G,·) ist zyklich wenn es ein a∈G gibt (das erzeugende Element) so, dass G={an|n∈ℤ}.
Die Gruppe (G,+) ist zyklich wenn es ein a∈G gibt (das erzeugende Element) so, dass G={n·a|n∈ℤ}, wobei n·a=a+a+...+a (n mal).
Bew.: Die Anzahl der Elemente jeder Untergruppe ist ein Teiler von p.
Beispiel: Die Drehgruppe regelmäßiger Vielecke.
Beispiel: Die Restklassengruppe (ℤn,+)
Beispiel:
1 2 3 4 5 2 3 4
Die von σ=( ) erzeugte Untergruppe U={id, σ, σ ,σ ,σ } von S
2 3 4 5 1 5
2 1 2 3 4 5 3 1 2 3 4 5 4 1 2 3 4 5 5
σ = ( ) σ = ( ) σ = ( ) σ = id
3 4 5 1 2 4 5 1 2 3 5 1 2 3 4
2 3 4
Hier: σ=(1→2→3→4→5) σ = (1→3→5→2→4) σ = (1→4→2→5→3) σ = (1→5→4→3→2)
Zyklische Permutationen
Beispiel: Die Permutation P∈S71 2 3 4 5 6 7 P=( ) = (Kurzbezeichnung) (2 1 3 5 4 7 6) 2 1 3 5 4 7 6lässt sich darstellen als Produkt der Transpositionen (Zweierzyklus=Transposition): P=(1→2)·(4→5)·(6→7).
Die Zyklen sind elementfremd, können also vertauscht werden.
Beispiel: Die Permutation P∈S7
1 2 3 4 5 6 7 P=( ) = (Kurzbezeichnung) (2 1 3 4 6 7 5) 2 1 3 4 6 7 5läßt sich darstellen als Produkt (1→2)·(5→6→7). Die Zyklen können vertauscht werden.
Satz: Jede Permutation aus Sn (n≥2) lässt sich darstellen als Produkt elementfremder Zyklen. Diese sind bis auf die Reihenfolge eindeutig bestimmt.
Achtung:
Zyklen mit gemeinsamen Elementen können nicht vertauscht werden: 1 2 3 4 1 2 3 4 ( )=(1→2→3)·(3→4)≠(3→4)·(1→2→3)=( ) 2 3 4 1 2 4 1 3
Beispiel einer Untergruppe,
die von einem Element erzeugt wird
1 2 3 4 5 2 1 2 3 4 5 3 1 2 3 4 5 4 1 2 3 4 5 5
P= ( ), P =( ), P =( ), P =( ), P = id
2 3 4 5 1 3 4 5 1 2 4 5 1 2 3 5 1 2 3 4
2 3 4
U={id, P, P , P , P } ist Untergruppe von S mit |U|=5
5
In Zyklenschreibweise:
2 3 4
P=(1→2→3→4→5), P =(1→3→5→2→4), P =(1→4→2→5→3), P =(1→5→4→3→2)
Der Satz von Cauchy
(Kunz 147, BAE 207)Satz: Ist die Ordnung |G| einer Gruppe G durch die Primzahl p teilbar, dann enthält G ein Element σ der Ordnung p. d.h. |{e,σ,σ2,...,σp-1}| = p.
σ ist zum Beispiel von der Ordnung 3, wenn σ3 = e (neutrales Element) ist, und die von σ erzeugte Gruppe {e,σ,σ2} 3 Elemente enthält.
Beweis: Der Beweis wird für p=3 geführt, kann aber ohne Einschränkung für eine Primzahl p erweitert werden. (Quelle WP)
Sei M={(a,b,c)|a,b,c∈G mit abc=e}. |M|=|G|2, da M={(a,b,(ab)-1|a,b∈G}.
Dann gilt: Aus abc∈M folgt abc=e, bca=a-1abca= a-1ea=e also (b,c,a)∈M und analog (c,a,b)∈M.
Ich kann also die Elemente in M zyklisch vertauschen.
Sei M0 ={(a,a,a)|a∈M}. Da (e,e,e)∈M0 folgt |M0|>0.
Da |M0| ein Teiler von |G| ist und 3 ein Teiler von |G| ist, gilt sogar 3 ist Teiler von |M0|.
Es gibt also ein a≠e mit a3=aaa=e ∎
Satz von Sylow
Ist die Ordnung |G| einer Gruppe G durch pk für eine Primzahl p und ein k≥1 teilbar, dann enthält G ein Element σ der Ordnung pk. (Quelle Gadmann S.68)Der Satz von Sylow ist also eine Verallgemeinerung des Satzes von Cauchy.
Normalteiler
Definition: Eine Untergruppe H von G heißt Normalteiler (in Zeichen H⊴G), wenn alle linken gleich wie alle rechten Nebenklassen sind, d.hH Normalteiler ⇔ Für alle a∈G ist a·H=H·a ⇔ Für alle a∈G ist a·H·a-1=H.
In diesem Fall sind die linken Nebenklassen aH und die rechten Nebenklassen Ha gleich: a·H=H·a (a∈G).Satz: Sei G/H = {aH|a∈G} die Menge aller Nebenklassen,
dann bilden diese mit der Verknüpfung (a·H)·(b·H)=a·b·H eine Gruppe. Das neutrale Element ist dann H.
Die Abbildung f: x→x·H ist dann ein Homomorphismus von G in G/H mit ker(f)=f-1{H}=H.
In abelschen Gruppen ist jede Untergruppe Normalteiler.
Wichtigstes Beispiel: 5ℤ ist Normalteiler von ℤ (diesmal additiv geschrieben).
Die Faktorgruppe H=ℤ/5ℤ wird mit ℤ5 bezeichnet. Beispiel für die Verknüfung:
(3+5ℤ)+(2+5ℤ)=5ℤ, da 3+2=0 mod 5.
Mit der Abkürzung k=k+ℤ ist ℤ5={ 0, 1, 2, 3, 4 }, häufig auch kurz notiert als ℤ5={0,1,2,3,4}.
2 oder auch 7 usw. ist ein Repräsentant von 2=2+ℤ. Wi die gewählt werden ist willkürlich.
Zum Beispiel ist auch möglich ℤ5={ 10, 6, -3, 23, 9 }
Die Faktorgruppe H=ℤ/5ℤ wird mit ℤ5 bezeichnet. Beispiel für die Verknüfung:
(3+5ℤ)+(2+5ℤ)=5ℤ, da 3+2=0 mod 5.
Mit der Abkürzung k=k+ℤ ist ℤ5={ 0, 1, 2, 3, 4 }, häufig auch kurz notiert als ℤ5={0,1,2,3,4}.
2 oder auch 7 usw. ist ein Repräsentant von 2=2+ℤ. Wi die gewählt werden ist willkürlich.
Zum Beispiel ist auch möglich ℤ5={ 10, 6, -3, 23, 9 }
Normalteiler nach WP
Nach WP
Normalteiler sind im mathematischen Teilgebiet der Gruppentheorie betrachtete spezielle Untergruppen.
Ihre Bedeutung liegt vor allem darin, dass sie genau die Kerne von Gruppenhomomorphismen sind.
In einer Gruppe G und jedem ihrer Normalteiler N kann die Faktorgruppe G/N gebildet werden.
Normalteiler sind im mathematischen Teilgebiet der Gruppentheorie betrachtete spezielle Untergruppen.
Ihre Bedeutung liegt vor allem darin, dass sie genau die Kerne von Gruppenhomomorphismen sind.
In einer Gruppe G und jedem ihrer Normalteiler N kann die Faktorgruppe G/N gebildet werden.
Beispiel: ℤ/3ℤ={0, 1,2} mit 0=3ℤ; 1=1+3ℤ und 2=2+3ℤ.
Der französische Mathematiker Évariste Galois erkannte im 19. Jahrhundert als erster die Wichtigkeit des Konzeptes „Normalteiler“ für die Untersuchung nicht-kommutativer Gruppen. In seiner Theorie zur Lösung algebraischer Gleichungen, der so genannten Galoistheorie, ist die Existenz von Normalteilern einer Gruppe von Permutationen (Galoisgruppe) entscheidend für die Lösbarkeit der Gleichung durch Radikale.N=A3 ist Normalteiler von G=S3
Nach Permutationen ist G={d0=id,d1,d2,s1,s2,s3} {3 Drehungen und 3 Spiegelungen} undN={d0,d1,d2} (3 Drehungen, d0=id wird als Drehung gezählt}
d1N={d1,d2,d0}=Nd1 entsprechend d2N=Nd2 und d3N=Nd3 und alle gleich N
s1N={s1,s2,s3}=Ns1=s2N={s2,s3,s1}={s2,s1,s3}
s2N={s2,s3,s1}=Ns2 und s2N{s3,s1,s2}=Ns2
Ergebnis: N ist Normalteiler und die Faktorgruppe G/N enthält zwei Elemente. Repräsitanten sind id und s1.
Beispiel für Untergruppe, die nicht Normalteiler ist
Gruppe S3={id,(1→2),(1→3),(2→3),(1→2→3),(1→3→2)}. Untergruppe H={id,(1→2)}⇒ (1→3)H(1→3)-1=(1→3)H(1→3)={id,(2→3)}≠H
FLA 20/2.1
Der Kern eines Homomorphismus
Sei f ein Homomorphismus von G in eine Gruppe (H,·)
Ker(f)={a∈G|f(a)=1} ist Normalteiler, nämlich
Satz: Sei N=Ker(f). Dann gilt für für alle g∈G: gNg-1=N
Beweis: Sei g∈G und n∈N. Dann gilt f(gng-1)=f(g)f(n)f(g-1)=f(g)*1*f(g)-1=1
Siehe auch Kleine Beweise
Beweis: Sei g∈G und n∈N. Dann gilt f(gng-1)=f(g)f(n)f(g-1)=f(g)*1*f(g)-1=1
Siehe auch Kleine Beweise
Gut zu wissen:
- Normalteiler von S3 sind nur {id}, A3 (die Drehungen) und S3.
- Normalteiler von S4 sind nur {id}=Kom(V), die Kleinsche Vierergruppe V=Kom(A4) mit 4 Elementen, A4=Kom(S4) mit 12 Elementen und S4 mit 4!=24 Elementen.
- Normalteiler von Sn für n=5,6,7,... sind nur {id}, An und Sn.
Auflösbare Gruppen
Zu jeder Gruppe G kann man die Kommutatorgruppe bilden.
-1 -1
G' = <{aba b |a,b∈G}> ist Normalteiler von G. "< >"heißt: wird erzeugt von ...
3
G''=(K(G')), G =K(G''), ...
n
Bricht diese Kette mit G = {id} ab, heißt die Gruppe auflösbar.
Satz:S4 ist auflösbar
Satz:S5 ist nicht auflösbar.
(FLA 140) Theorem von Feit und Thomson (1963): Jede endliche Gruppe von ungerader Ordnung ist auflösbar. (Der Originalbeweis ist 255 Seiten lang).
Erzeugendes System für S5
Satz: Ein 5-er-Zyklus und eine Transposition erzeugen S5 (Gilt auch fürPrimzahl p statt 5). (Artin S. 45).
1 2 3 4 5 1 2 3 4 5
Beispiel: a=(1→2→3→4→5)=( ) b=(1→2)=( )
2 3 4 5 1 2 1 3 4 5
1 2 3 4 5 2 1 2 3 4 5 2 1 2 3 4 5 2 1 2 3 4 5
ab=( ) a =( ) ba =( ) a b=( ) usw.
3 2 4 5 1 3 4 5 1 2 4 5 1 2 3 4 3 5 1 2
Artin S.45: Wenn man zeigen kann, dass die Galoisgruppe (als Gruppe G in S5) eines Polynoms 5. Grades einen 5-er-Zyklus und eine Transposition besitzt, dann ist G=S5 und die Lösungen des Polynoms nicht durch Radikale darstellbar.
A5
A5 - die Kommutatorgruppe von S5 - ist die Symmetriegruppe des Ikosaeders.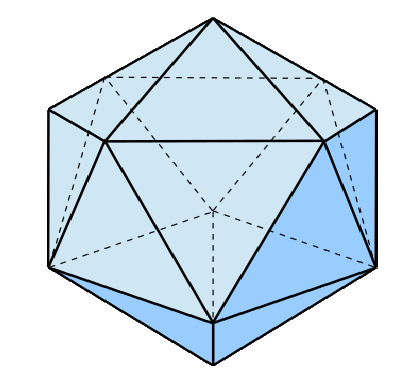
Das Isokaeder ist ein platonischer Körper, der aus 20 gleichseitigen Dreiecken gebildet wird, wobei jeweis 5 Dreiecke um einen Eckpunkt angeordnet sind. Es besitzt 20 Flächen (Dreiecke), 30 Kanten und 12 Eckpunkte.
Die Drehgruppe des Ikoseders (”Ikosaedergruppe”) besteht aus allen Drehungen im Raum, die ein fest gewähltes Ikosaeder (mit Mittelpunkt in O) in sich überfuhren.
Diese Gruppe hat 60 Elemente. Die 12 Ecken können vertauscht werden und zusätzlich noch um die Ecken gedreht werden, die die 5 Dreicke ineinander überführen. Diese Gruppe ist isomorph zu A4.
Nebenbei bemerkt: Die 5 Platonischen Körper sind:
- Tetraeder (Vierflächner, Oberfläche aus vier Dreiecken)
- Würfel (Hexaeder, Sechsflächner, Oberfläche aus sechs Quadraten)
- Oktaeder (Achtflächner, Oberfläche aus acht Dreiecken)
- Dodekaeder (Zwölfflächner, Oberfläche aus zwölf Fünfecken)
- Ikosaeder (Zwanzigflächner, Oberfläche aus zwanzig Dreiecken)
Homomorhismus bei Gruppen
Eine Abbildung f:G→H von eine Gruppe (G,∘) in eine Gruppe (H,×) heißt Homomorphismus, wenn gilt:f(a∘b)=f(a)×f(b) für alle a,b∈G
F heißt Isomorphismus, wenn ein Homomorphismus g:H→G existiert, so dass fog=idH und gof=idG.Ein Isomorphismus von G auf G heißt Automorphiamus.
Beispiel 1:
Beispiel 2: f(x)=ex ist ein Homomorphismus von (ℝ,+) in (ℝ,*).
Es gilt nämlich:f(a+b)=ea+b=ea*eb=f(a)*f(b).
f ist sogar ein Isomorphismus von (ℝ,+) in (ℝ+,*), wobei ℝ+={x∈ℝ|x positiv}.
Die Umkehrabbildung ist g:(ℝ+,*)→(ℝ,+) mit g(x)=ln(x).
Man sieht hier am Beispiel e0=1, dass bei einem Homomorphismus das neutrale Element der ersten Gruppe auf das neutrale Element der zweiten Gruppe übertragen wird.
Beispiel 3: Sei I die Menge der musikalischen Intervalle (Terz, Quinte, Oktave usw.). Die Addition ist die Hinereinanderausführung.
f(große Terz + kleine Terz)=f(Quinte), nämlich 5/4*6/5=3/2.
f(12 Quinten)=(3/2)12 ist etwas größer als f(7 Oktaven)=27 (siehe hier..).
Auch hier gilt: Bild des neutralen Elements = neutrales Element der Bildgruppe: Frequenzverhältnis(Prim)=1.
2
f: x→x ist ein Homomorphismus von (ℝ,·) in (ℝ,·), es ist nämlich
2 2 2
f(xy)=(xy) = x y =f(x)f(y)
Beispiel 2: f(x)=ex ist ein Homomorphismus von (ℝ,+) in (ℝ,*).
Es gilt nämlich:f(a+b)=ea+b=ea*eb=f(a)*f(b).
f ist sogar ein Isomorphismus von (ℝ,+) in (ℝ+,*), wobei ℝ+={x∈ℝ|x positiv}.
Die Umkehrabbildung ist g:(ℝ+,*)→(ℝ,+) mit g(x)=ln(x).
Man sieht hier am Beispiel e0=1, dass bei einem Homomorphismus das neutrale Element der ersten Gruppe auf das neutrale Element der zweiten Gruppe übertragen wird.
Beispiel 3: Sei I die Menge der musikalischen Intervalle (Terz, Quinte, Oktave usw.). Die Addition ist die Hinereinanderausführung.
i→f(i)
Intervall→Frequenzverhältnis von i
f(große Terz + kleine Terz)=f(Quinte), nämlich 5/4*6/5=3/2.
f(12 Quinten)=(3/2)12 ist etwas größer als f(7 Oktaven)=27 (siehe hier..).
Auch hier gilt: Bild des neutralen Elements = neutrales Element der Bildgruppe: Frequenzverhältnis(Prim)=1.
Einfache Gruppen
Nur als Beispiel, mit was sich heutige Mathematiker beschäftigen.Definition: Gradmann (S.76) Eine Gruppe ist einfach, wenn sie nur sich selbst oder {id} als Normalteiler hat.
Beispiel:
Die zyklische Gruppe ℤp für eine Primzahl p.
Die Gruppe An für n≠4 (Beweis: Kunz S. 144)
Die Gruppe aller Invertierbaren Matrizen mit der Determinante 1 über dem Körper ℤ7
Die kleinste einfache Gruppe, die nicht von dieser Form ist, hat Ordnung 7920.
Alle einfachen Gruppen wurden bis zum Jahr 1982 klassifiziert. Kunz S. 145: Die Klassifizierung ist mehrere tausen Seiten lang.
Die Größte hat mehr als 800 000 Oktillionen Elemente, genau hat sie
808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 Nonill. Okt. Sept. Sext. Quint. Quadr. Trill. Billion MillionElemente und wird Monstergruppe genannt.
Die zweitgrößte, das "Babymonster" hat
4 154 781 481 226 426 191 177 580 544 000 000 Elemente. ≈ 4 155 Sextillionen