Die Homepage von Joachim Mohr
Basiswissen klassische Mathematik
Was blieb bei Ihnen hängen?
Ein kleiner Test.
I
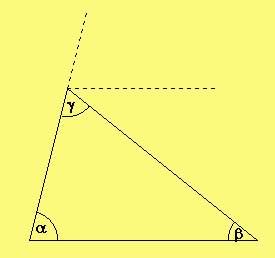
Formuliere und beweise
den Winkelsummensatz!
Tipp: Beachte die Hilfslinie und erinnere Dich an Stufen- und Wechselwinkel!
Lösung
II
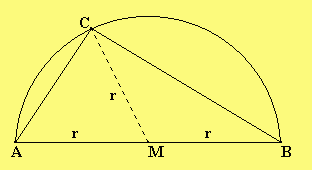
Formuliere und beweise
den Satz des Thales!
Beachte: Die Hilfslinie MC teilt das Dreieck in zwei gleichschenklige Teildreiecke. Dort sind die Basiswinkel gleich.
Lösung
III
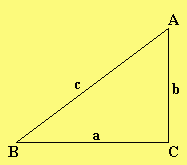
Formuliere und beweise
den Satz des Pythagoras!
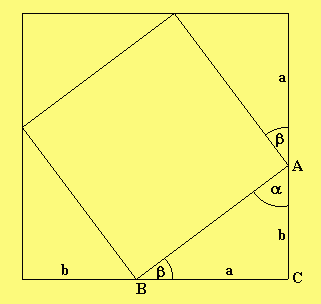
Setzte zum Beweis vier gleiche rechtwinklige Dreiecke so zusammen, dass sie nebenstehendes Quadrat mit der Seitenlänge (a+b) bilden.
Bemerkung zu den Winken: Im rechtwinkligen Dreieck ist α+β=90°. Deshalb hat das Viereck über c vier 90°-Winkel und ist tatsächlich ein Quadrat.
Hinweis: Das große Quadrat hat einen Flächeninhalt von (a+b) 2 und setzt sich auch vier rechtwinkligen Dreiecken und dem Quadrat über der Seite c zusammen.
Lösung
IV Etwas anspruchsvoller ist der Schwerpunktsatz und der Sinus- und Kosinussatz.
Wir gehen weiter zu einem Satz aus der Zahlentheorie.
V Für eine zusammengesetzte Zahl n=a·b (a, b ε N, a ≤ b) gilt: a2≤ n
Will man zum Beispiel prüfen ob 401 eine zusammengesetzte Zahl ist (also keine Primzahl), genügt es zu testen, ob eine der Zahlen von 2 bis 20 Teiler von 401 ist, es genügt sogar zu prüfen, ob eine der Primzahlen 2,3,5,7,11,13,17 oder 19 Teiler von 401 ist. (Dies ist nicht der Fall: also ist 401 Primzahl.)Beachte zum Beweis, dass a2 ≤ n gleichbedeutend ist mit a ≤ √ n (a, n ε N).
Zeige, dass es für a·b = n unmöglich ist dass sowohl a > √ n als auch b > √ n ist.
Lösung
