Die Homepage von Joachim Mohr  
≡
Basiswissen

Der goldene Schnitt

Basiswissen klassische Mathematik
Lösungen

Der goldene Schnitt

I
Der Winkelsummensatz:
Die Winkelsumme im Dreieck ist 180°
α + β + γ = 180°

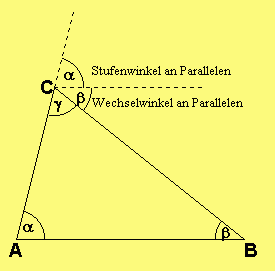
Winkelsummensatz
Beweis: ( Gleich weite Winkel werden als gleich bezeichnet.)
Die Winkel α bei den Punkten A und C sind als Stufenwinkel gleich.
Die Winkel β bei den Punkten B und C sind als Wechselwinkel gleich.
Beim Punkt C sieht man:
α + β + γ = gestreckter Winkel
α + β + γ = 180°

II
Der Satz des Thales:
Der Winkel im Halbkreis ist ein Rechter.
Der Innenwinkelwinkel bei C des Dreiecks ABC ist 90°

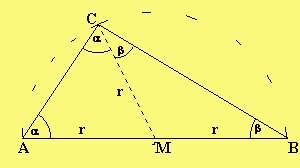
Satz des Thales
Beweis:
Die Winkel α bei den Punkten A und C sind als Basiswinkel des gleichschenkligen Dreiecks AMC gleich.
Die Winkel β bei den Punkten B und C sind als Basiswinkel des gleichschenkligen Dreiecks MBC gleich.
Nach dem Winkelsummensatz ist die Winkelsumme im Dreieck 180°: α+β+(α+β) =180°
Somit ergibt sich für den Innenwinkel bei C: α+β =90°

III
Der Satz des Pythagoras

Satz des Pythagoras Satz des Pythagoras 
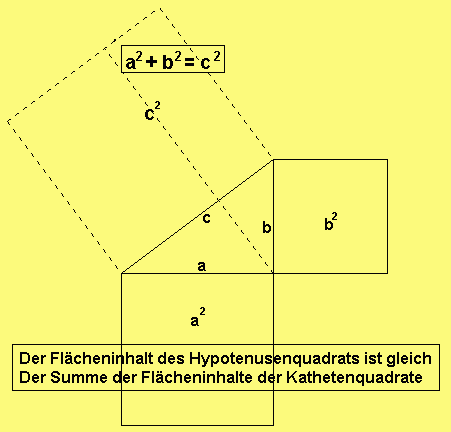
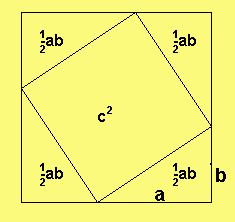
Beweis:Der Flächeninhalt des

grossen Quadrats ist

     2   2         2
(a+b) = a + 2ab + b

  und ist gleich

  2    1      2
 c + 4·-ab = c + 2ab.
       2

     2          2    2
Aus a  + 2ab + b  = c  + 2ab
folgt:

a 2 + b 2 = c 2

Ein weiterer Beweis des Satzes von Pythagoras

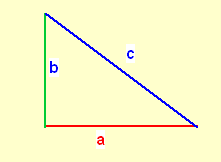
5pythagoras1
Wenn Sie lieber mit der Schere arbeiten: Schneiden Sie dieses Dreieck aus und zeichnen Sie es in dieser Lage auf ein Blatt Papier. Drehen Sie es dann um 90° im Uhrzeigersinn und legen Sie die grüne Seite auf die rote des gezeichneten ganz nach rechts und zeichnen Sie es wieder auf das Papier. Wiederholen Sie dies noch zwei mal bis Sie die folgende Figur erhalten.
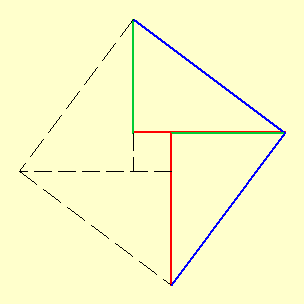
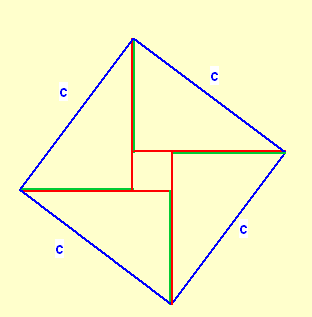
Pythagoras2 Pythagoras3
Das blaue Quadrat hat den Flächeninhalt c2
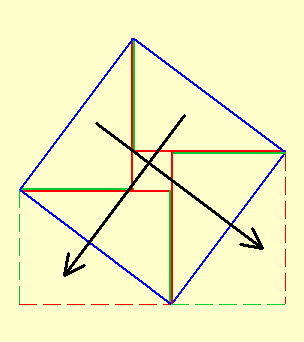
5pythagoras4a
Schneiden Sie nun das linke obere Dreieck aus und verschieben Sie es in Pfeilrichtung.
Dasselbe machen Sie mit dem rechten oberen Dreieck. Sie erhalten dann folgende Figur, die aus zwei Rechtecken und einem Quadrat besteht. Das kleine Quadrat hat die Seitenlänge (b-a).
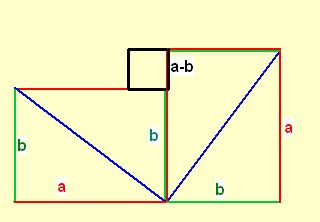
Pythagoras5
Das blaue Quadrat mit dem Flächeninhalt c2 wurde neu gruppiert in zwei Rechtecke und einem Quadrat.
Die zwei Rechtecke und das Quadrat haben zusammen den Flächeninhalt:
a·b + b·a + (a-b)2 = 2a·b + (a-b)2.
Somit: c2 = 2a·b + (a-b)2 = 2a·b + a2 - 2a·b + b2

c2 = a2 + b2


IV
der Schwerpunktsatz!

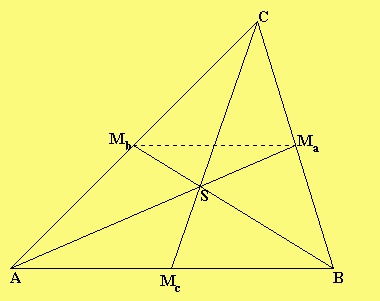
Schwerpunktsatz
Der Schwerpunkt teilt die Schwerelinien im Verhältnis 1:2.
Also: M a S : SA = 1 : 2, M b S : SB = 1 : 2 und M c S : SC = 1 : 2

Beweis: Da Mb Mitte von AC ist, ist CMb: CA = 1 : 2.
Nach dem 2. Strahlensatz also
Mb Ma : AB = CMb : CA = 1 :2
und in einer zweiten Figur:
Ma S : SA = Ma Mb : AB = 1 : 2.

Vektorieller Beweis siehe Schwerpunktsatz.

V Für eine zusammengesetzte Zahl n=a·b (a, b ε N) gilt a ≤ √n oder b ≤ √n

Widerspruchsbeweis:

Wir nehmen an, dass für n= a·b sowohl a > √n als auch b > √n ist und leiten daraus eine Widerspruch her.

Ist nämlich a > √n und b > √n, so folgt daraus: a·b > √n· √n, also a·b > n.

Das ist ein Widerspruch zu der Annahme: n = a·b. ∎