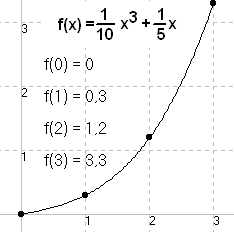Joachim Mohr Mathematik Musik
Zur Einführung: Logarithmus
Umkehrfunktionen
1. einführendes Beispiel:
2 + +
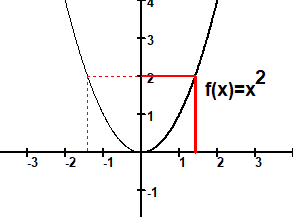
f(x)=x Definitionsbereich (hier) D =ℝ ={x∈R|x≥0}, Wertebereich W =ℝ .
f 0 f 0
Wenn der Funktionswert bekannt ist - z.B. f(x)=2 - so kann x berechnet werden.
2
f(x)=x = 2 ⇒ x=√2.
Der Wert x=-√2 ist ausgeschlossen, da er nicht im Definitionsbereich ist.
(Das ist auch der Grund, dass der Definitionsbereich von f eingeschränkt wurde.)
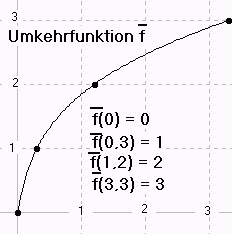
Allgemein gilt y=f(x) ⇔ x=√y.
—
Die Umkehrfunktion von f ist also y → √y oder (mit Vertauschen von x und y)
-1 — +
f (x)= √x für x∈ℝ .
0
-1 -1
Es gilt hier - wie für alle Umkehrfunktionen - f(f (x))=x und f (f(x))=x, nämlich
——
-1 — — 2 -1 -1 2 / 2
f(f (x)) = f(√x))=(√x) = x und f (f(x))=f (x )=√ x = x.
-1
Grundsätzlich gilt: Definitionsbereich von f = Wertebereich von f
-1
Wertebereich von f = Definitionsbereich von f.
2. einführendes Beispiel:
Kleine Vorübung: lg(x) ist die Zahl mit der ich 10 potenzieren muss, damit ich x erhalte.Also lg(1000)=3, lg(105)=lg(100 000)=5. Allgemein: lg(10x)=x.
Umgekeht: 10lg(1000) = 103=1000. Allgemein: 10lg(x) = x.
x
—
3 +
f(x)=10 Definitionsbereich D =ℝ, Wertebereich W =ℝ .
f f
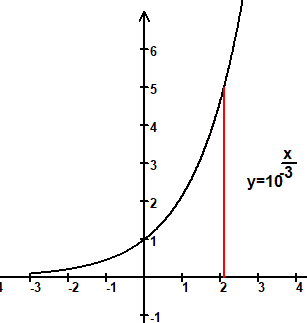
Was muss ich für x einsetzen, dass z.B. f(x)=5 ist?
x x
— —
3 3 x x
10 =5 ⇒ lg(10 )=lg(5) ⇒ —·lg(10)=lg(5) ⇒ —·1=lg(5) ⇒x=3·lg(5)≈2,1
3 3
Berechnung der Umkehrfunktion erfolgt über die Gleichung f(x)=y ⇔ x=f-1(y).
x x
— —
3 3 x x
10 =y ⇒ lg(10 )=lg(y) ⇒ —·lg(10)=lg(y) ⇒ —=lg(y) ⇒x=3·lg(y)
3 3
-1 -1
Also ist f (y)=3·lg(y) oder f (x)=3·lg(x)
x
—
3 +
Die Umkehrfunktion von f(x)=10 mit D = R und W = ℝ ist
f f
-1 +
f (x) = 3·lg(x) mit D = ℝ und W = ℝ.
-1 -1
f f
-1 -1
Es gilt hier wieder - wie für alle Umkehrfunktionen - f(f (x))=x und f (f(x))=x, nämlich
x x
— —
-1 lg(x) -1 -1 3 3 x
f(f (x)) = f(3·lg(x)) = 10 = x und f (f(x)) = f (10 ) = 3·lg(10 )=3·—=x.
3
Allgemein
