Die Homepage von Joachim Mohr
Seite mit den Aufgaben
Zum Ausdrucken
Sinus- und Kosinussatz
Alle Sätze und Beweise sind "Folklore"
Vorbemerkungen:
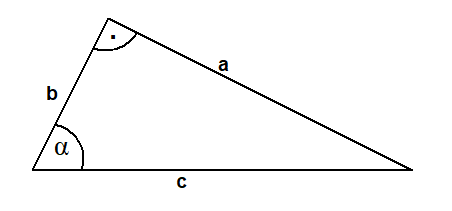
für Winkel zwischen 0° und 90° definiert.
In der Figur ist gezeigt, wie der Definitionsbereich im Einheitskreis für beliebige Winkel erweitert wird.
a b b
sinα=— , cosα=—, tanα=—
c c a
sin2α+cos2α=1
Beweis:
2 2 2 2
2 2 a b a + b
sin α + cos α = —— + —— = —————— = 1,
2 2 2
c c c
2 2 2
da nach dem Satz von Pythagoras a + b = c
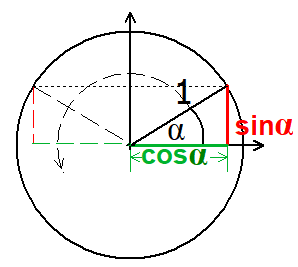
für Winkel zwischen 0° und 90° definiert.
In der Figur ist gezeigt, wie der Definitionsbereich im Einheitskreis für beliebige Winkel erweitert wird.
sin(180°-α)=sin(α) sin(180°+α)=-sin(α) sin(360°-α)=-sin(α)
cos(180°-α)=-cos(α) cos(180°+α)=-cos(α) cos(360°-α)=cos(α)
tan(18°-α)=-tan(α) tan(180°+α)=tan(α) tan(360°-α)=-tan(α)
Zum Beispiel:
sin(150°)=sin(30°) sin(210°)=-sin(30°) sin(330°)=-sin(30°)
cos(150°)=-cos(30°) cos(210°)=-cos(30°) cos(330°)=cos(30°)
tan(150°)=-tan(150° tan(210°)=tan(30°) tan(330°)=-tan(30°)
Weiter gilt natürlich: sin(360°+α)=sin(α) cos(360°+α)=cos(α)
tan(360°+α)=tan(α) usw.
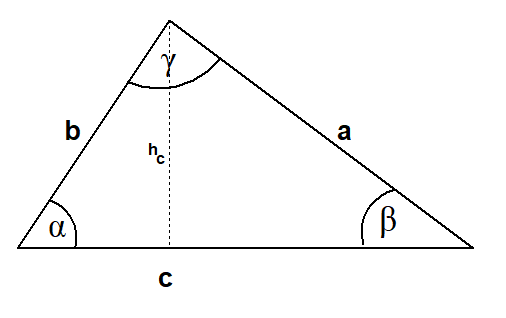
Sinussatz
In dem eingezeichneten Dreieck gilt
sinα sinβ sinγ
———— = ———— = ————
a b c
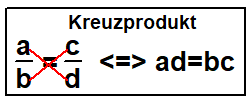
Beweis: Mit der eingezeichneten Höhe hc auf c folgt
h h
c c
sinα=—— und sinβ=——
b a
⇒ hc=b·sinα=a·sinβ
sinα sinβ ———— = ———— ∎ a b Ganz ähnlich kann man zeigen: sinα sinγ ———— = ————. a c
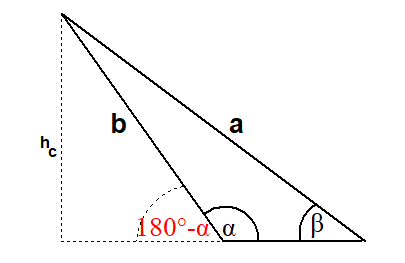
h h
c c
sin(180°-α)=—— und sinβ=——
b a
Da sin(180°-α)=sinα kann man wieder zeigen
sinα sinβ
———— = ————.
a b
Kosinussatz
2 2 2 a = b +c -2bcsinα
Beweis:
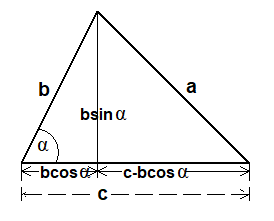
Durch die Höhe auf c wird das Dreieck in zwei rechtwinlige Dreiecke geteilt.
Im linken rechtwinkligen Dreieck sind die Katheten
bsinα und bcosα.
Im rechten rechtwinligen Dreieck Dreieck sind die Katheten
bsinα und c-bcosα.
Nach dem Satz des Pythagoras gilt:
2 2 2 2 a = b sin α + (c-b·cosα) ⇒ 2 2 2 2 2 2 a = b sin α + c -2cb·cosα +b cos α 2 2 2 2 2 a = b (sin α + cos α) + c - 2bccosα 2 2 2 a = b + c - 2bccosα ∎ Entsprechnend gelten die Formeln: 2 2 2 b = a + c - 2accosβ und 2 2 2 c = a + b - 2abcosγ
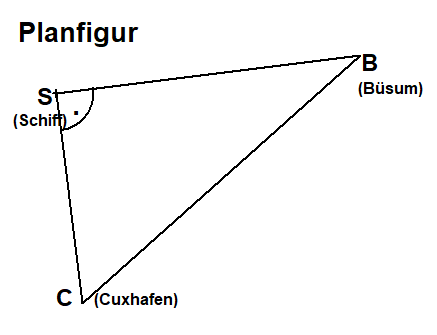
Aufgabe1
Entfernung Büsum-Cuxhafen BC=29,3kmWinkel von Schiff nach Cuxhafen und Büsum: ∠CSB=90°
Winkel aus Cuxhaven zwischen dem Hafen Büsum und dem Schiff: ∠SCB=43°
Frage: Wie weit ist das Schiff von Büsum enrtfernt: SB=???
Lösung:
SB SB
Dann sieht man sin(43°)= —— = ——————
BC 29,3km
Also: SB=29,3km·sin(43°) = 20,0 km
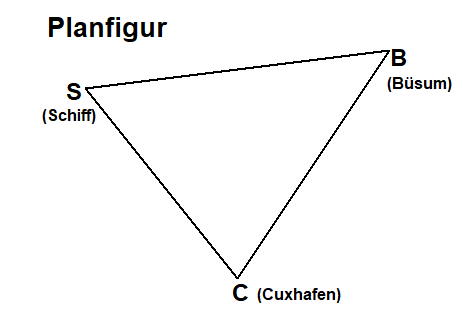
Aufgabe 2
Entfernung Büsum-Cuxhafen BC=29,3km
Winkel von Schiff nach Cuxhafen und Büsum: ∠CSB=47°
Winkel aus Cuxhaven zwischen dem Hafen Büsum und dem Schiff: ∠SCB=71°
Frage: Wie weit ist das Schiff von Büsum enrtfernt: SB=???
Lösung: Sinussatz
sin(47°) sin(71°)
———————— = ———————— ⇒ sin(47°)*SB = sin(71°)*29,3km
29,3km SB
(Kreuzprodukt)
sin(71°)
⇒ SB = ————————*29,3km = 37,9 km
sin(47°)
Seite mit den Aufgaben
Zum Ausdrucken
Berechne die fehlenen Seitengrößen und Winkel
Faustregel: Die Rechnung erfolgt mit 4 geltenden Ziffern. Das Endergebnis wird dann mit 3 geltenden Ziffern angegeben.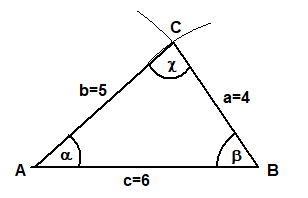
SSS Gegeben: Alle drei Seiten
Gegeben (in cm): a=4, b=5 und c=6Berechnung:
2 2 2
Aus a = b +c -2bc·cos(α) folgt
2 2 2
b + c - a
cos(α)=————————— = 0,75 ⇒ α=41,41°
2bc
sin(α) sin(β)
Aus —————— = —————— folgt
a b
b
sin(β)=—sin(α)=0,8268 ⇒ β=55,77° und γ=180°-α-β=82,82°
a
Ergebnis: α=41,4°, β=55,8°, γ=82,8°
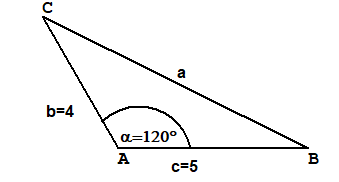
SWS Gegeben Zwei Seiten und der eingeschlossene Winkel
Gegeben (in cm):b=4, c=5 und α=120°.Berechnung:
2 2 2
a = b +c -2bc·cos(α)=61 ⇒ a=7,810
sin(β) sin(α) b
Aus ——————=—————— folgt sin(β)=—sin(α)=0,4435
b a a
⇒ β=26,33° und γ=180°-α-β=33,67°
Ergebnis: a=7,81 β=26,3°, γ=33,7°
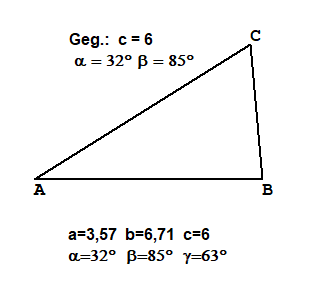
WSW Gegeben Eine Seiten und zwei anliegende Winkel
Gegeben (in cm):c=6, α=32°, β=85°Berechnung:
γ=180°-α-β=63°
a c
Aus —————— = —————— folgt
sin(α) sin(γ)
sin(α)
a=——————c=3,568
sin(γ)
b c
Aus —————— = —————— folgt
sin(β) sin(γ)
sin(β)
b=——————c=6,708
sin(γ)
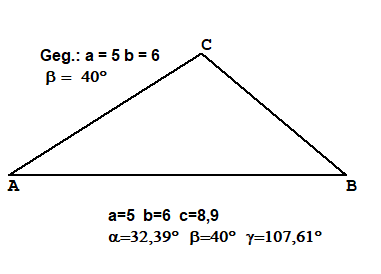
Ssw Gegeben Zwei Seiten gegenüber der größeren Seite den Winkel
Gegeben (in cm):a=5, b=6, β=40°Berechnung:
sin(α) sin(β)
Aus —————— = —————— folgt
a b
a
sin(α)=—sin(β)=0,5357 ⇒ α=32,39°
b
γ=180°-α-β=107,61°
c b sin(γ)
Aus —————— = —————— folgt c=——————b=8,897
sin(γ) sin(β) sin(β)
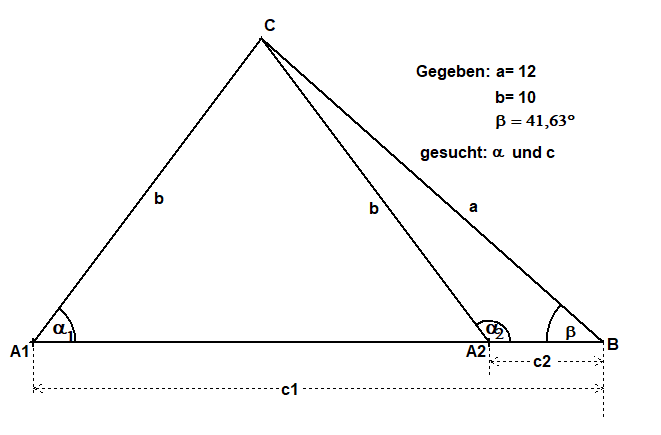
Ssw Gegeben Zwei Seiten gegenüber der kleineren Seite den Winkel
Gegeben (in cm):a=12, b=10, β=42°Rechnung:
sin(α) sin(β)
Aus —————— = ——————
a b
a
folgt sin(α)=—sin(β)=0,7972
b
α =52,86° und α =180°-α =127,14°
1 2 1
γ =85,51° γ =11,23°
1 2
c b
Aus —————— = —————— folgt
sin(γ) sin(β)
sin(γ)
c=——————b
sin(β)
Also c =15,01 und c =2,932
1 2
Weitere gerechnete Beisiele
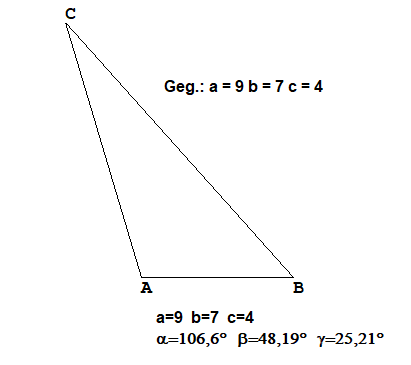
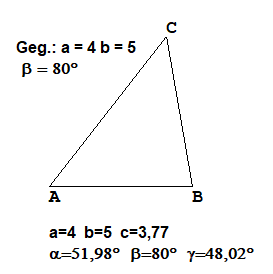
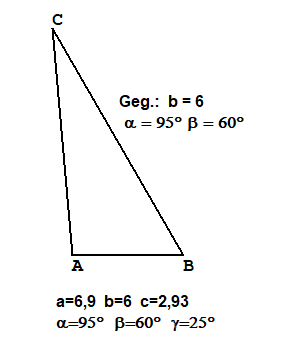
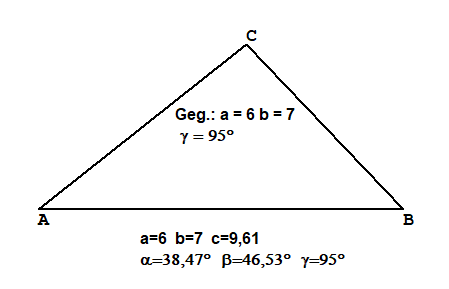
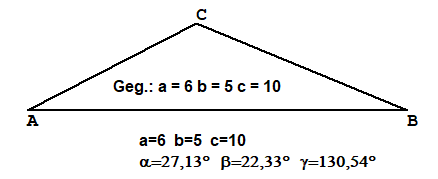
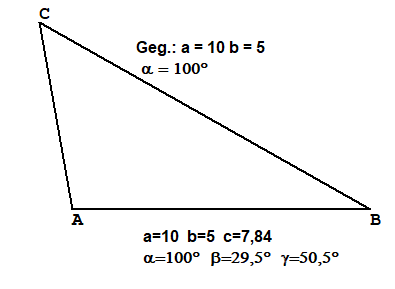
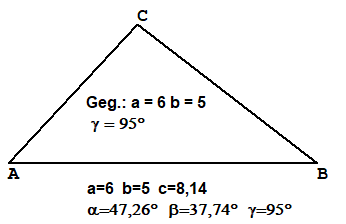
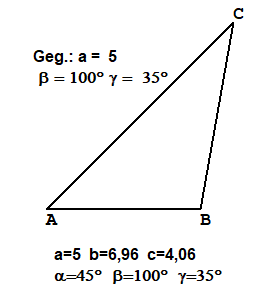
Die Beispiele wurden mit TTGeo erstellt
Der Aufruf ist etwas versteckt unter dem Menüpunkz "Drei Punkte"