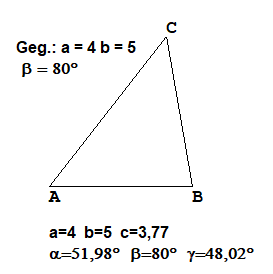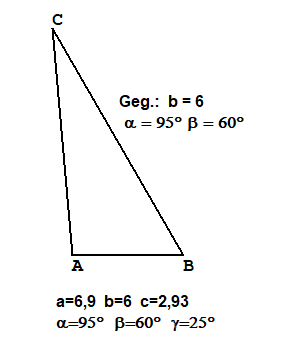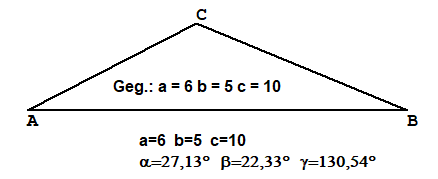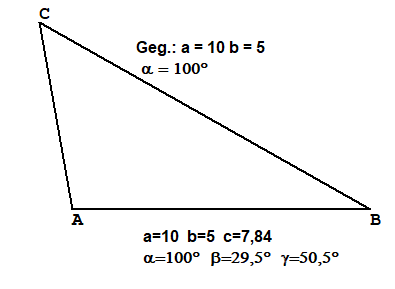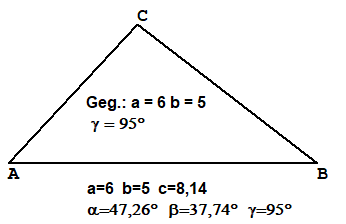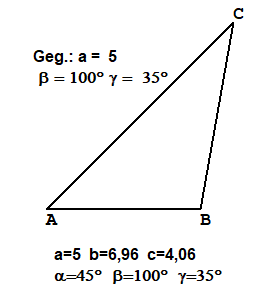Die Homepage von Joachim Mohr
zurück
Berechne die fehlenen Seitengrößen und Winkel
Faustregel: Die Rechnung erfolgt mit 4 geltenden Ziffern. Das Endergebnis wird dann mit 3 geltenden Ziffern angegeben.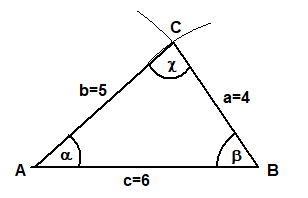
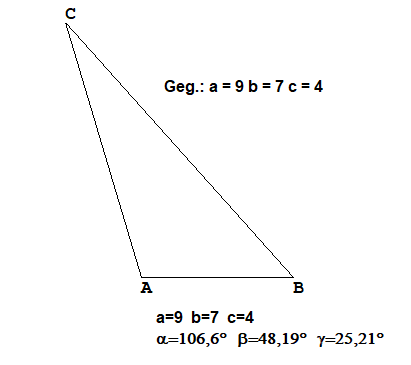
SSS Gegeben: Alle drei Seiten
Gegeben (in cm): a=4, b=5 und c=6Berechnung:
2 2 2
Aus a = b +c -2bc·cos(α) folgt
2 2 2
b + c - a
cos(α)=————————— = 0,75 ⇒ α=41,41°
2bc
sin(α) sin(β)
Aus —————— = —————— folgt
a b
b
sin(β)=—sin(α)=0,8268 ⇒ β=55,77° und γ=180°-α-β=82,82°
a
Ergebnis: α=41,4°, β=55,8°, γ=82,8°
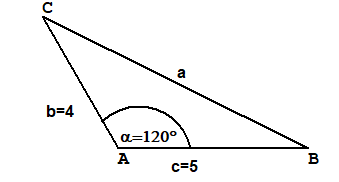
SWS Gegeben Zwei Seiten und der eingeschlossene Winkel
Gegeben (in cm):b=4, c=5 und α=120°.Berechnung:
2 2 2
a = b +c -2bc·cos(α)=61 ⇒ a=7,810
sin(β) sin(α) b
Aus ——————=—————— folgt sin(β)=—sin(α)=0,4435
b a a
⇒ β=26,33° und γ=180°-α-β=33,67°
Ergebnis: a=7,81 β=26,3°, γ=33,7°
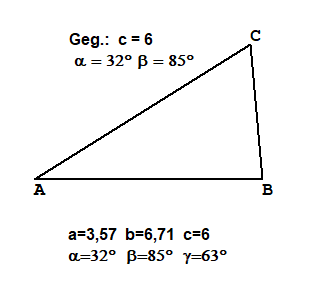
WSW Gegeben Eine Seiten und zwei anliegende Winkel
Gegeben (in cm):c=6, α=32°, β=85°Berechnung:
γ=180°-α-β=63°
a c
Aus —————— = —————— folgt
sin(α) sin(γ)
sin(α)
a=——————c=3,568
sin(γ)
b c
Aus —————— = —————— folgt
sin(β) sin(γ)
sin(β)
b=——————c=6,708
sin(γ)
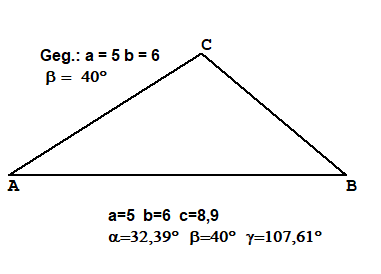
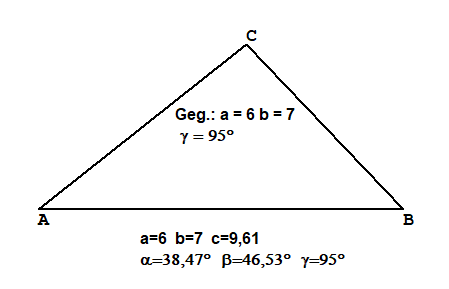
Ssw Gegeben Zwei Seiten gegenüber der größeren Seite den Winkel
Gegeben (in cm):a=5, b=6, β=40°Berechnung:
sin(α) sin(β)
Aus —————— = —————— folgt
a b
a
sin(α)=—sin(β)=0,5357 ⇒ α=32,39°
b
γ=180°-α-β=107,61°
c b sin(γ)
Aus —————— = —————— folgt c=——————b=8,897
sin(γ) sin(β) sin(β)
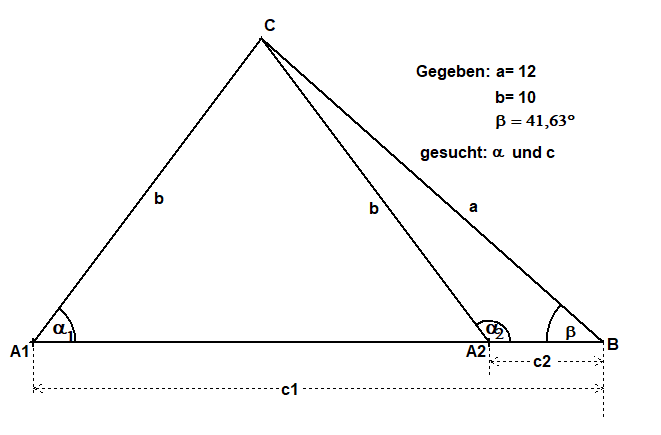
Ssw Gegeben Zwei Seiten gegenüber der kleineren Seite den Winkel
Gegeben (in cm):a=12, b=10, β=42°Rechnung:
sin(α) sin(β)
Aus —————— = ——————
a b
a
folgt sin(α)=—sin(β)=0,7972
b
α =52,86° und α =180°-α =127,14°
1 2 1
γ =85,51° γ =11,23°
1 2
c b
Aus —————— = —————— folgt
sin(γ) sin(β)
sin(γ)
c=——————b
sin(β)
Also c =15,01 und c =2,932
1 2
Weitere gerechnete Beisiele