Die Homepage von Joachim Mohr
|
Kettenbrüche |

|
Siehe auch:
Programm zur Berechnung von Kettenbrüchen mit bedeutenden Beispielen: TTMathe
Beweis
I Einführung
Satz: Jede rationale Zahl lässt sich auf genau eine Weise in einen endlichen regulären Kettenbruch entwickeln.Beispiel:
43 13 1 1 1
—— = 1 + —— = 1 + ———— = 1 + —————— = 1 + ————————
30 30 30 4 1
—— 2 + —— 2 + ————
13 13 1
3 +-
4
= 1+1/(2+1/(3+1/4))
Er wird abgekürzt zu [1,2,3,4].
Der Kettenbruch heißt regulär, wenn in den Zählern immer eine 1 steht. Der letzte Nenner muss wegen der Eindeutigkeit natürlich größer 1 sein.
Ein berühmter nicht regulärer Kettenbruch ist
π 1 —— = 1 + —————————————————— 4 4 2 + ——————————————— 9 2 + ——————————— 16 2 + ——————— 2 + ...
Satz: Jede irrationale reelle Zahl lässt sich auf genau eine Weise in einen unendlichen regulären Kettenbruch entwickeln.
Zum Beispiel:
-
\/2 = [1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...]
-
\/5 - 1
——————— = [0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...]
2
e = [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14,1,1,16,1,1,18,...]
Satz: Jeder unendliche Kettenbruch [v ,v ,v ,...]
1 2 3
konvergiert (v , v , v , ... ε N).
1 2 3
Bemerkenswert ist, dass die Teilwerte um den Grenzwert alternieren, so dass
man eine optimale Abschätzung für den Grenzwert erhält.
II Berechnung des Kettenbruches aus Zähler A und Nenner B
(Beliebige reelle Zahl siehe III)Dass man die Koeffizienten nach dem Euklidischen Algorithmus berechnen kann, sieht man an folgender Rechnung:
43 13 1 1 1
—— = 1 + —— = 1 + ———— = 1 + —————— = 1 + ————————
30 30 30 4 1
—— 2 + —— 2 + ————
13 13 1
3 +-
4
Euklidischer Algorithmus: Allgemein:
43 = 1·30 + 13 A = v1·B + r1
30 = 2·13 + 4 B = v2·r1 + r2
13 = 3·4 + 1 r1 = v3·r2 + r3
4 = 4·1 + 0 ...
43
Und somit: —— = [1,2,3,4]
30
A
Die allgemeine rekursive Berechnung des Kettenbruches - = [v , v , v , ...]
B 1 2 3
ist nach dem Euklidischen Algorithmus folgende:
r = A; r = B (Anfangswerte) sowie
-1 0
v = r div r und r = r mod r für n > 0 (bis r = 0)
n n-2 n -1 n n - 2 n - 1 n+1
Erklärung: a div b bedeutet die ganzzahlige Division zweier ganzer Zahlen
a mod b = a - (a div b)*b ist der "Rest" bei der Division
(Danke nach Mü für den Korrekturhinweis)
Zum Beispiel: 30 div 13 = 2, 30 mod 13 = 4,
da 30:13 = 2 Rest 4
function BruchZuKettenbruch_nur_theoretisch(const a,b: integer): string;
//nicht empfohlen
var n: integer;
function r(n: integer): integer; //n >= -1
begin
if n = -1 then result := a else
if n = 0 then result := b else
result := r(n - 2) mod r(n-1);
end;
function v(n: integer): integer;
begin
result := r(n-2) div r(n-1)
end;
begin
n := 1;
result := '[';
repeat
result := result + inttostr(v(n)) + ',';
inc(n);
until r(n) = 0;
result := result + inttostr(v(n)) + ']';
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
edit1.text := BruchZuKettenbruch_nur_theoretisch(77708431,2640858);
end;
Beachte jedoch: Die Effizienz
des Programms ist schlecht. (r(n) und v(n) müssen stets vom Startwert neu berechnet werden,
obwohl sie vorher schon berechnet wurden).
Effizienter ist die iterative Berechnung:
Algorithmus zur Berechnung des Kettenbruches A/B
Zum Beispiel soll für A/B=43/30 berechnet werden: kettenbruch=[1,2,3,4]
Setze Anfangswerte: kettenbruch = '[' (Die Anfangsklammer) ra = A rb = B Wiederhole ... v = ra div rb (ganzzahlige Division) Füge zu kettenbruch die Zahl v dazu (ab der zweiten Zahl vorher ein Komma) r = ra mod rb (r ist der Rest bei Divsion von ra durch rb) (Schreibe die Werte für ra und rb folgendermaßen fort) ra=rb rb=r ... bis r = 0 Füge zu kettenbruch noch die Abschlussklammer ] dazu.In Delphi als Funktion BruchZuKettenbruch geschrieben mit Aufrufebeispiel:
function BruchZuKettenbruch(const a,b: integer): string; //empfohlen
var ra, rb, r, v: integer;
begin
result := '[';
ra := a;
rb := b;
repeat
v := ra div rb;
if length(result) > 1 then result := result + ',';
result := result + inttostr(v);
r := ra mod rb;
ra := rb;
rb := r;
until r = 0;
result := result + ']';
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
edit1.text := BruchZuKettenbruch(77708431,2640858);
end;
Mit diesem Programm gerechnetes Beispiel:
(von Christaan Huygens)
77708431/2640858 = [29,2,2,1,5,1,4,1,1,2,1,6,1,10,2,2,3]
1
= 29+————————————————————————————————
1
2+——————————————————————————————
1
2+————————————————————————————
1
1+——————————————————————————
1
5+————————————————————————
1
1+——————————————————————
1
4+————————————————————
1
1+——————————————————
1
1+————————————————
1
2+——————————————
1
1+————————————
1
6+——————————
1
1+————————
1
10+—————
1
2+———
1
2+-
3
=29+1/(2+1/(2+1/(1+1/(5+1/(1+1/(4+1/(1+1/(1+1/(2+1/(1+1/(6
+1/(1+1/(10+1/(2+1/(2+1/3)))))))))))))))
III Berechnung des (endlichen oder unendlichen) Kettenbruches einer beliebigen reellen Zahl q
43
Das Beispiel von oben mit q = —— wandeln wir entsprechend ab.
30
Dazu verwenden wir folgende Funktionen:
int(x) = der ganzzahlige Anteil von x, frac(x) = der Rest.
Genau: int(x) = die größte ganze Zahl kleiner oder gleich x.
frac(x) = x - int(x).
Zum Beispiel: int(2,789) = 2 und frac(2,789) = 0,789
Wir wandeln den weiter oben aufgeführten Euklidischen Algorithmus ab:
statt ...
Euklidischer Algorithmus: Allgemein:
43 = 1·30 + 13 A = v1·B + s1
(r1 wird unten "gebraucht")
30 = 2·13 + 4 B = v2·r1 + s2
13 = 3·4 + 1 r1 = v3·r2 + s3
4 = 4·1 + 0 ...
... schreiben wir:
43 13
—— = 1 + —— q = v1 + r1
30 30
30 4
—— = 2 + —— q1 = v2 + r2
13 13
13 1
—— = 3 + - q2 = v3 + r3
4 4
4
- = 4 + 0 q3 = v4 + r4
1
...
Abbruch, falls r = 0
n
Die Variablen q , v und r berechnen sich aus
n n n
dem Ausgangswert q folgendermaßen:
1
v1 = int(q) r1 = frac(q) q1 = ——
r1
1
v2 = int(q1) r2 = fraq(q1) q2 = ——
r2
1
v3 = int(q2) r3 = fraq(q2) q3 = ——
r3
... Solange bis r = 0.
n
Falls stets r ≠ 0 ist, erhalten wir einen
n
unendlichen Kettenbruch
Unser Algorithmus wird also abgewandelt zu:
q = v1 + r1 mit v1 = int(q) und r1 = frac(q)
1
q1 = v2 + r2 mit q1 = ——, v2 = int(q1) und r2 = frac(q1)
r1
1
q2 = v3 + r3 mit q2 = ——, v3 = int(q2) und r3 = frac(q2)
r2
u.s.w.
Es ergibt sich also:
1 1 1
q = v1 + —— = v1 + ——————— = v1 + ———————————— ...
q1 1 1
v2 + —— v2 + ———————
q2 1
v3 + ——
q3
= [v1, v2, v3, ...]
Der Rest r wird bei rationalem q irgendwann 0,
n
dann ist der Kettenbruch endlich.
Bei irrationalem q wird der Kettenbruch unendlich.
Unser Beispiel nun mit diesem Algorithmus berechnet:
43 1
—— = 1 + —————————
30 1
2 + —————
1
3 + -
4
43 13
q = —— = v1 + r1 mit v1 = 1 und r1 = ——
30 30
30 4
q1 = —— = v2 + r2 mit v2 = 2 und r2 = ——
13 13
13 1
q2 = —— = v3 + r3 mit v3 = 3 und r3 = ——
4 4
4
q3 = - = v4 + r4 mit v4 = 4 und r4 = 0.
1
Unser abgewandelter Algorithmus zur Berechnung des Kettenbruches von q
lautet "theoretisch" demnach folgendermaßen:
Theoretisch richtig, numerisch aber grobe Fehler im Sinne der numerischen Mathematik!
Setze Anfangswert: kettenbruch = '[' (Die Anfangsklammer) Wiederhole ... v = int(q) r = frac(q) Füge zu kettenbruch die Zahl v dazu (ab der zweiten Zahl vorher ein Komma) falls r = 0 schließe ab, sonst q = 1/r ... bis maximal 25 Schritte (zum Beispiel) Abschluss: Füge zu kettenbruch noch die Abschlussklammer ] dazu.Was sind hier für Fehler im Sinne der Numerik gemacht wortden?
Rechnet man mit diesen Algorithmus das Beispiel für q = 43/30, dann erhält man statt q = [1,2,3,4] den unendlichen Kettenbruch
q = [1,2,3,4,26214,2,2,101,1,1082,3,1,4,1,3,11,2,1,1,1,2,2,1,2,2,1...]
oder q = [1,2,3,3,1,-1717986919,1,1,1,1,25,-1068060651,1,...]
je nachdem man mit geringerer oder höherer Genauigkeit rechnet.
Verfolgen wir die Rechnung im Einzelnen:
Einfache Genauigkeit (ungefähr 7 bis 8 signifikanten Stellen)
Computerrechnung Theoretisch : v=1 1 r=0,43333328 13/30 q=2,30769253 30/13 v=2 2 r=0,30769253 4/13 q=3,24999762 13/4 v=3 3 r=0,24999762 1/4 q=4,00003815 4 v=4 4 r=0,00003815 0 Prüfe nie, ob eine reelle Zahl Null ist!! q=26214,400 undefiniert (1/0) ....Die erste Regel lautet:
Prüfe nicht "r=0" sondern "|r| 〈 0.0000001" (je nach Genauigkeit)!
Die doppelte Genauigkeit (ungefähr 15-16 signifikante Stellen) zeigt noch eine weitere fatale Fehlerursache:
Computerrechnung Theoretisch v=1 1 r=0,4333333333333333 13/30 q=2,3076923076923075 30/13 v=2 2 r=0,3076923076923075 4/13 q=3,2500000000000022 13/4 v=3 3 r=0,2500000000000022 1/4 q=3,9999999999999645 4 v=3 4 Katastrophe! r=0,9999999999999645 0 q=1,0000000000000355 nicht definiert v=1 r=0,0000000000000355 q=28147498000000 v=-1717986919 Überlauf, da "ganze Zahl" (Integer) zu groß ...Die Ursache der "Katastrophe" ist die Unstetigkeit der Funktion "int[x]".
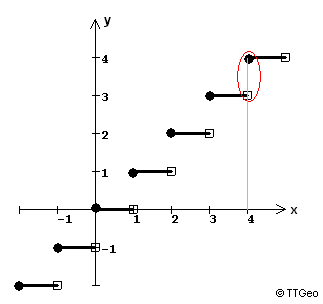
f(x) = int(x) "Treppenfunktion"
häufig auch zitiert als
f(x) = [x] "Gauß'sche Klammerfunktion"
Beachte:
f(x) = 4 für x = 4
f(x) = 3 für x = 4 - ε für 0 〈 ε ≤ 1. Zum Beispiel
f(x) = 3 für x = 3,9999999999999645
1 1
Es ist int(-) = 4 aber int(——————————————————) = 3
4 0,2500000000000022
Die zweite Regel lautet: Überlege bei unstetigen Funktionen stets, was Rechenungenauigkeiten
bewirken können.
Wir ändern unseren Algorithmus also folgendermaßen ab:
Berechnung des Kettenbruchs von q: Setze Anfangswert: kettenbruch = '[' (Die Anfangsklammer) Wiederhole ... v = int(q) Falls |v + 1 - q| 〈 0.0000001 (Je nach Rechengenauigkeit), setzte v = v+1 r = q - v Füge zu kettenbruch die Zahl v dazu (ab der zweiten Zahl vorher ein Komma) falls |r| 〈 0.00000001 (je nach Rechengenauigkeit) schließe ab, sonst q = 1/r ... bis maximal 25 Schritte (zum Beispiel) Abschluss: Füge zu kettenbruch noch die Abschlussklammer ] dazu.In Delphi als Funktion BruchZuKettenbruch geschrieben mit Aufrufebeispiel:
function BruchZuKettenbruch(q: extended): string;
const Max = 20;
eps = 1E-5;
var n, v: integer;
r: extended;
begin
result := '[';
n := 0;
repeat
v := trunc(q);
//Hinweis: Rechnerisch trunc(x) = int(x),
//jedoch liefert int(x) eine Realzahl, trunc(x) eine Integerzahl
if abs(v+1-q) 〈 eps then v := v + 1;
if length(result) > 1 then result := result + ',';
result := result + inttostr(v);
r := q-v;
if abs(r) 〈 eps then Begin
result := result + ']';
exit;
End;
q := 1/r;
form1.memo1.lines.add('v=' + inttostr(v) + #13#10 +
'r='+formatfloat(aa,r)+#13#10+
'q='+formatfloat(aa,q));
inc(n);
until n > Max;
result := result + ',...]';
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
edit1.text := BruchZuKettenbruch(exp(1));
end;
eps = 1E-5 und Max = 20 sind haben sich durch Probieren als günstig
erwiesen. Man muss sich jedoch bewußt sein, dass sich Rechenungenauigkeiten
sehr schnell aufaddieren.
IV Bruchnäherung einer reellen Zahl
Es gibt verschiedene Gründe, eine Zahl x durch einen Bruch anzunähern.- Christaan Huygens konnte mit weniger Zähnen bei Zahnrädern auskommen als theoretisch notwendig war.
- Aus der Dezimaldarstellung von Brüchen, die wegen Rundungsfehler nicht mehr ganz exakt sind, kann wieder der ursprüngliche (einfache) Bruch gewonnen werden.
- Transzendente Zahlen, deren Kettenbruchentwicklung periodisch ist, können aus der Kettenbruchentwicklung leicht berechnet werden.
a1 a2 a3
Die Näherungsbrüche ——, ——, ——,....
b1 b2 b3
(a1,a2,a3,...,b1,b2,b3,... natürliche Zahlen) sind
a1 v1
—— = ——
b1 1
a2 1 v2·v1 + 1 v2·a1 + 1
—— = v1 + - = ————————— = —————————
b2 v2 v2 v2
a3 1 v1*v2*v3+v1+v3 v3·a2 + a1
—— = v1 + ——————— = ——————————————— = ——————————
b3 1 v2*v3+1 v3*b2 + 1
v2 + ——
v3
a4 v4·a3 + a2
—— = ... = ——————————
b4 v4·b3 + b2
a5 v5·a4 + a3
—— = ... = ——————————
b5 v5·b4 + b3
a
n
Die Zähler a und Nenner b von p = [v , v , v , ..., v ] = ——
n n 1 2 3 n b
n
können also rekursiv aus v , v , v , ..., v berechnet werden.
1 2 3 n
a = v , b = 1 Anfangswert 1 1 1 a = v ·a + 1, b = v Anfangswert 2 2 1 2 2 a = v ·a + a , b = v ·b + b für n = 3,4,5,... n n n-1 n-2 n n n-1 n - 2Der allgemeine Beweis wird mit Hilfe der vollständiger Induktion über die "Länge" n des Kettenbruchs mit folgender Beziehung geführt.
a
n+1 1
———— = [v , v , ... , v ] = v + ———————————————————
b 1 2 n+1 1 [v , v , ..., v ]
n+1
2 3 n+1
In Delphifunktion BruchZuKettenbruch wird dann einfach abgewandelt zu:
//Für Testzwecke. Siehe unten die Funktion "DezimalzuBruch"
function BruchZuKettenbruch(q: extended): string;
const Max = 20;
eps = 1E-5;
var n, v: integer;
a,b,am,bm,amm,bmm: integer;
r: extended;
begin
result := '[';
n := 0;
a := 1;
b := 0;
am := 0; //altes a
bm := 1; //altes b
repeat
v := trunc(q);
if abs(v+1-q) 〈 eps then v := v + 1;
if length(result) > 1 then result := result + ',';
result := result + inttostr(v);
r := q-v;
amm := am; //uraltes a
bmm := bm; //uraltes b
am := a; //altes a
bm := b; //altes b
a := v*am+amm;
b := v*bm+bmm; // Näherungsbruch a/b
form1.memo1.lines.add('Stufe '+ inttostr(n)+' ergibt Näherung ' +
inttostr(a) + '/' + inttostr(b));
if abs(r) 〈 eps then Begin
result := result + ']';
exit;
End;
q := 1/r;
inc(n);
until n > Max;
result := result + ',...]';
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
edit1.text := BruchZuKettenbruch(Pi);
end;
Wollen Sie nur zu einer Dezimalzahl q (positiv oder negativ)
einen bestmöglichen Bruch a/b als
Näherungswert berechnen, dann verwenden Sie die folgende Prozedur
DezimalzuBruch(q: extended, var a,b: integer):boolean;Falls etwas schiefgeht (zum Beispiel Integerüberlauf) oder der angenäherte Bruch zu ungenau ist, liefert die Funktion als Ergebnis false, im Erfolgsfall true.
function DezimalzuBruch(const q0: extended; var a,b: integer):boolean;
const Max = 20;
eps1 = 1E-5; //durch Probieren anpassen!
eps2 = 1E-15;
var n, v: integer;
am,bm,amm,bmm: integer;
q, qabs, r: extended;
//Der Näherungsbruch a/b wird fortlaufend verbessert.
//am/bm altes a/b, amm/bmm uraltes a/b
begin
result := false; //Nur im Erfolgsfall: true
//Anfangswerte
n := 0;
a := 1;
b := 0;
am := 0;
bm := 1;
qabs := abs(q0); //Zunächt nur |q0|=a/b
q := qabs;
repeat
try
v := trunc(q);
//trunc(q) liefert den ganzzahligen Anteil von q als Integer
if abs(v+1-q) 〈 eps1 then v := v + 1; //trunc(3.99999999) wird zu 4
r := q-v;
//Vor der berechnung von a/b wird a/b wird zu am/bm(alt)
//vorher am/bm wird zu amm/bmm (uralt)
amm := am;
bmm := bm;
am := a;
bm := b;
a := v*am+amm;
b := v*bm+bmm; // Besserer Näherungsbruch a/b
if abs(qabs-a/b) 〈 eps2 then Begin //gewünschte Genauigkeit erreicht
if q0 〈 0 then a := -a;
result := true;
exit;
End;
{if b > 10000 then Begin //Abbruchbedingung für 3stelligen Nenner
a := am; //altes a
b := bm; //altes b
if q0 〈 0 then a := -a;
result := true;
exit;
End;}
q := 1/r;
inc(n);
except a:=0; b := 1 ;exit End;
until n > Max;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x: extended;
a,b: integer;
begin
x := -77708431/2640858; //oder x=Pi (Dann "{" und "}" entfernen
if DezimalzuBruch(x,a,b) then
edit1.text := floattostr(x) + '=' + inttostr(a) + '/' + inttostr(b) else
edit1.text := floattostr(x) + ': Keinen Bruch gefunden';
end;
Hier geht man davon aus, dass q der Bruch a/b ist bis auf die Rechenungenauigkeit
des Computers.
Wollen Sie zum Beispiel einen Näherungswert für Pi, bei dem der Nenner höchstens dreistellig sein soll, dann müssen Sie folgende Abbruchbedingung "aktivieren".
if b > 10000 then Begin a := am; //altes a b := bm; //altes b result := true; exit; End;
