Joachim Mohr Mathematik Musik

TTMathe

Mathematik und Geometrie

Das Rechenprogramm in Analysis und Vektorrechnung für Abiturienten und Studienanfänger.

Plattform: Windows 95 bis Windows 10 (Stand: Juni 2016)

Rechnen	Schaubild mit ...	Lineare Gleichungssystem	Gleichung
Ergebnisse mit ...	... Kurvenscharen	Lösung wird vorgerechnet	Lösung wird vorgerechnet
... Brüchen	... Wertetafel		quadratisch
... PFZ	... Kurvendiskussion		kubisch (Cardano)
... Wurzeln	... Integral		4.Grades
Geometrie	Algebra	Rechenblatt	Kettenbrüche
Berechnungen mit ...	Polynommultiplikation	Beispiel	zum Beispiel für Pi
... Vektoren	Polynomdivision	a=sqrt(5/3)	Pi=[3,7,15,1,...]
... Geraden	pythag. Zahlentripel	b=sin(45°)	Pi ungefähr 22/7
... Ebenen	pythag. Zahlenquadrupel	c=a+b	besser: 333/106
... Kugeln	Ausgleichsgerade	(-27)^(1/2)	besser: 355/113
Eigenwerte		(auch komplexe Zahlen)
Zeichnungen

Ausführlich

Schaubilder

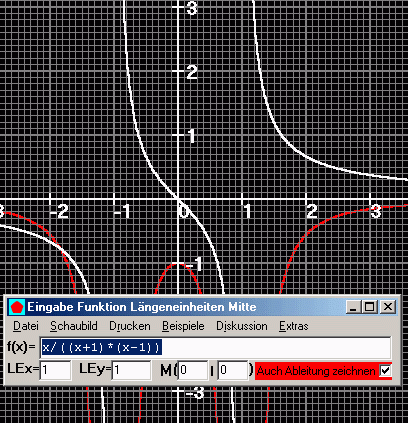
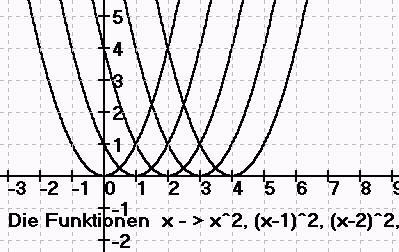
Lineare Gleichungssysteme

n=5 (Zahl der Unbekannten) m=4 (Zahl der Gleichungen)
1/2   -0.5   0      0     -0,5     1/2
0      0     -1      1     -1      1/3
10/9   0    -20/9    0     10/9    1/4
0     20      0    -10    -10      1/5
(Lösung: siehe unten)

Downloadseite TTMathe

Mit TTMathe können Sie leicht:

Rechnen: Term eingeben.
- Ergebnisse auch als Brüche.
- Wurzeln werden teilweise radiziert und Nenner rational.
- Parameter möglich (als Speicher).
- Standardfunktionen (einschließlich Binominialverteilung und Gaußscher Summenfunktion) integriert
- Verlauf wird gespeichert.
- Primfaktorenzerlegung.
Schaubilder zeichnen. Beliebig viele Schaubilder können gleichzeitig (mit Schaubild der Ableitung) gezeichnet werden.
Wertetafeln (mit Ableitung) erstellen (Ergebnisse auch als Brüche)

Nullstellen, Hoch-, Tief- und Wendepunkte und Integrale berechnen

Beispiel:
   f(x)=-x^4+8/3*x^3-16/9*x^2+24/9*x-7/9
   Nullstellen (f(x)=0 und VZW von f):
      N1(1/3|0;2,22222222651872851)  Tangente: y=2,222*x-0,741
      N2(7/3|0;-12,8888883073330351) Tangente: y=-12,889*x+30,074
   Punkte mit waagrechter Tangente (f'(x)=0 und VZW von f'):  H(1,708102|3,36738)
   Wendepunkte (f''(x)=0 und VZW von f''):
       W(0,2818|-0,1142;2,2105) Tangente: y=2,21*x-0,737
       W(1,0516|1,9386;3,1228)  Tangente: y=3,123*x-1,345
   (1. und 2. Ableitung wird nür näherungsweise berechnet, daher keine Bruchdarstellung)
   Integral von 1/3 bis 7/3 über f(x) = 3,970 370 370 370 [Fehler ~ -4E-12]

Lineares Gleichungssysteme lösen (Ergebnisse auch als Brüche)
Beispiel LGS (Eingabewerte einfach überschreiben!)
n=5 (Zahl der Unbekannten) m=4 (Zahl der Gleichungen)

1/2	-0.5	0	0	-0,5	\|1/2
0	0	-1	1	-1	\|1/3
10/9	0	-20/9	0	10/9	\|1/4
0	20	0	-10	-10	\|1/5

TTMathe rechnet folgende Lösung  aus:
    x1=2689/1800  +3*x5              =1,493 889 + 3*x5
    x2=889/1800   +2*x5              =0,493 889 + 2 *x5
    x3=571/900    +2*x5              =0,634 444 + 2 *x5
    x4=871/900    +3*x5              =0,967 778 + 3*x5
    x5 beliebig

Rechenblätter berechnen lassen.

Neu (Version 2007/08): Rechnen mit komplexen Zahlen

Im Beispiel wird der linke Teil vorgegeben. Der rechte wird dann berechnet.

  1. Beispiel: quadratische Gleichung
a=7                             7
b=-10                           -10
c=1                             1
d=b*b - 4a*c                    72
q=sqrt(d)                       8,485 281 374 238 570 29 = 6*sqrt(2)
x1=(-b+q)/(2*a)                 1,320 377 241 017 040 74 = (5+3*sqrt(2))/7
x2=(-b-q)/(2*a)                 0,108 194 187 554 387 836 = (5-3*sqrt(2))/7
  2. Beispiel: Heronverfahren
a=2                             2
x=1                             1
x=1/2(x+a/x)                    1,5 = 3/2
x=1/2(x+a/x)                    1,416 666 666 666 666 67 = 17/12
x=1/2(x+a/x)                    1,414 215 686 274 509 8 = 577/408
x=1/2(x+a/x)                    1,414 213 562 374 689 91 = 665857/470832
x=1/2(x+a/x)                    1,414 213 562 373 095 05 = sqrt(2)
Probe=x^2                             2
  3. Beispiel: Wahrscheinlichkeitsrechnung
            n über k (Beachte a=b mit "nue"=Funktion n über k)
a=fak(49)/(fak(6)*fak(49-6))    13 983 816
n=49                            49
b=nue(6)                        13 983 816
            Binominialverteilung(Beachte a=b und c=d mit Funktionen "Bin" und "BiS")
n=20                            20
k=6                             6
p=1/6                           0,166 666 666 666 666 667 = 1/6
a=nue(k)*p^k*(1-p)^(n-k)        0,064 705 145 989 495 228
b=Bin(k)                        0,064 705 145 989 495 228
c=Bin(0)+Bin(1)+Bin(2)+Bin(3)   0,566 545 637 775 669 321
d=BiS(3)                        0,566 545 637 775 669 321

Sie können auch beliebig genau rechnen. Zum Beispiel:

             Rechenblatt mit 60 Dezimalstellen
q=sqrt(5)  2,236067977499789696409173668731276235440618359611525724270897
a=(1+q)/2  1,618033988749894848204586834365638117720309179805762862135449
b=(1-q)/2  -0,618033988749894848204586834365638117720309179805762862135449
n=200            200
fib=(a^n-b^n)/q  280571172992510140037611932413038677189525,0->
         ->00000000000000014651132704405917234892126696587015810107122

Folgende Terme bei Berechnungen werden automatisch gefunden:

    Brüche
6*(1/2+1/3+1/5+4/7)         =9,628571429        =337/35
    Wuzeln
sqrt(108/5)                 =4,647580015        =6/5*sqrt(15)
1/2*sqrt(3/5)               =0,387298335        =1/10*sqrt(15)
sqrt(3/2)+sqrt(5/4)         =2,34277886         =1/2*sqrt(5)+1/2*sqrt(6)
   Trigonometrische Funktionen
sin(60°)                    =0,866025404        =1/2*sqrt(3)
sin(15°)                    =0,258819045        =1/4*sqrt(6)-1/4*sqrt(2)
cos(15°)                    =0,965925826        =1/4*sqrt(2)+1/4*sqrt(6)
tan(15°)                    =0,267949192        =2-sqrt(3)
sin(18°)                    =0,309016994        =1/4*sqrt(5)-1/4
arcsin(1/2)                 =0,523598776=1/6*Pi Ergebnis Winkel im Bogenmaß
arcsi_(1/2)                 =30                 Ergebnis Winkel im Gradmaß
    10-/2-/nat. Logarithmen
lg(7000)                    =3,84509804         =3+lg(7)
lg(1001)                    =3,000434077        =lg(7)+lg(11)+lg(13)
lg(sqrt(7))                 =0,42254902         =1/2*lg(7)
ln(4,5)                     =1,504077397        =2*ln(3)-ln(2)
lb(12)                      =3,584962501        =2+lb(3)
ln(12)                      =2,48490665         =2*ln(2)+ln(3)

(Die Terme werden heuristisch aus dem 18-stelligen Zahlenwert ermittelt)

Folgende nach Aufforderung (benötigt längere Zeit):

sin(3°)	=0,052335956	=1/16(sqrt(2)(sqrt(5)-1)(sqrt(3)+1)-2(sqrt(3)-1)*sqrt(5+sqrt(5)))
sin(84°)	=0,994521895	=1/8(sqrt(2)sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(85,5°)	=0,996917334	=1/8(sqrt(2)sqrt(2+sqrt(2))sqrt(5+sqrt(5))+(sqrt(5)-1)sqrt(2-sqrt(2)))
cos(3°)	=0,998629535	=1/16(sqrt(2)(sqrt(5)-1)(sqrt(3)-1)+2(sqrt(3)+1)*sqrt(5+sqrt(5)))
cos(84°)	=0,104528463	=1/8(sqrt(2)sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
tan(6°)	=0,105104235	=1/2(sqrt(2)sqrt(5-sqrt(5))-sqrt(3)*(sqrt(5)-1))
tan(9°)	=0,15838444	=-1/4(sqrt(2)(sqrt(5)+1)sqrt(5+sqrt(5))-4(sqrt(5)+1))
tan(81°)	=6,313751515	=1/4(sqrt(2)(sqrt(5)+1)sqrt(5+sqrt(5))+4(sqrt(5)+1))
etc,

(Die Terme werden heuristisch aus dem 18-stelligen Zahlenwert ermittelt)

Abstände von Punkten, Geraden und Ebenen im Raum berechnen und veranschaulichen

Sie klicken auf "Dreieck":

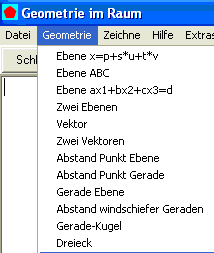
Dann erscheint folgendes Skript:

Dreieck A(6|4|4) B(2|6|5) C(3|4|1)
Überschreiben Sie die Zahlen und
klicken Sie dann auf "Rechnen"

Klick auf "Rechnen" liefert folgenden Text:

Dreieck A(6|4|4) B(2|6|5) C(3|4|1)
auf Ebene: 2*x1+5*x2-2*x3=24
BC=(1 -2 -4)       a=sqrt(21)=4,58257569496
AC=(-3 0 -3)       b=3*sqrt(2)=4,24264068712
AB=(-4 2 1)        c=sqrt(21)=4,58257569496
               Winkel
alpha=62,424 952 289 523 242 207°
beta=55,150 095 420 953 515 59°
gamma=62,424 952 289 523 242 203°
               Seitenhalbierenden
Strecke A(6|4|4) Ma(2'1/2|5|3)
Strecke B(2|6|5) Mb(4'1/2|4|2'1/2)
Strecke C(3|4|1) Mc(4|5|4'1/2)
Umkreis U(3'13/22|4'8/11|3'9/22)
r=7/22*sqrt(66)=2,58492131057
Kreis U(3,591|4,727|3,409)
r=2,585 orthogonal zu v(2 5 -2)
            SCHWERPUNKT(3'2/3|4'2/3|3'1/3)
Ha(2'4/7|4'6/7|2'5/7)  ha=3/7*sqrt(77)=3,760699
Hb(4'1/2|4|2'1/2)      hb=1/2*sqrt(66)=4,062019
Hc(4'2/7|4'6/7|4'3/7)  hc=3/7*sqrt(77)=3,760699
Dreiecksfläche=3/2*sqrt(33)=8,61684396981

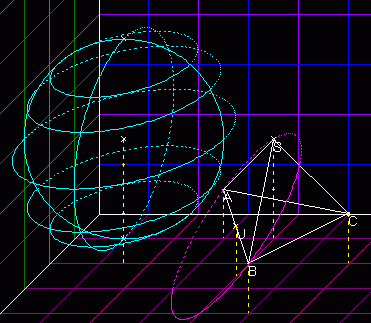
Sie klicken auf "Kugel durch ABCD":

Dann erscheint folgendes Skript:

Kugel durch A(4|4|6) B(0|3|6) C(5|4|5) D(-1|3|1)
Ändern Sie die Werte und klicken Sie dann auf "Rechnen"!

Klick auf "Rechnen" liefert folgenden Text:

Kugel durch A(4|4|6) B(0|3|6) C(5|4|5) D(-1|3|1)
Ansatz Kugel: x1^2+x2^2+x3^2+ax1+bx2+cx3=d
 => M(-a/2|-b/2|-c/2) r=d(A,M)
Punktprobe mit A,B,C und D führt mit Umformung
ax1+bx2+cx3-d=-(x1^2+x2^2+x3^2) auf das LGS für a,b,c und d:
n=4 m=4
4     4     6     -1 |-68
0     3     6     -1 |-45
5     4     5     -1 |-66
-1    3     1     -1 |-11
(1)-(2), (1)-(3), (1)-(4) führt auf das LGS für a,b und c:
n=3 m=3
4     1     0    |-23
-1    0     1    |-2
5     1     5    |-57
Lösung: a=-4 b=-7 c=-6
        in (1) => d=-12
KUGEL M(2|3'1/2|3) r=3,64
KUGEL M(2|3'1/2|3) Radius r=1/2*sqrt(53)=3,64005494464

 
Beispiel Ebene Parameterform -> Ebenengleichung:
         Sie rufen folgendes Beispiel auf und überschreiben die Werte:
Ebene Parameterform  p(4 2 3)    u(-3 -1 2)       v(-5 -4 1)
                     Aufpunkt    Richtungsvektor  Richtungsvektor
         TTMathe rechnet:
Koordinatengleichung der Ebene x1 - x2 + x3 = 5
Beispiel Ebene durch drei Punkte -> Ebenengleichung:
          Sie lassen sich folgendes Beispiel zeigen:
Ebene DREIECK  A(-1|3|-4)B(2|-5|3)C(1|-3|2), überschreiben die Werte und
erhalten die Koordinatengleichung  3x1 + 2x2 + x3 = -1
Beispiel Abstand Punkt Ebene:
       Sie rufen folgendes Beispiel auf und überschreiben die Werte:
2 -1 -5 3   <—— Diese Werte überschreiben: Ebene E: 2x1-x2-5x3=3
-1 2 1      <—— Diese Werte übreschreiben: Punkt P(-1 2 1)
         TTMathe rechnet:
Abstand = 2/5*sqrt(30) = 0,565685424
Fußpunkt = F(-1/5|1'3/5|-1) = F(-0,2|1,6|-1) (s=2/5)
Beispiel windschiefe Geraden:
         Sie rufen folgendes Beispiel auf und überschreiben die Werte:
Gerade p(9 10 -2)  u(-2 1 0)  Gerade g: x=p+s*u
Gerade q(1 -3 -4)  v(0 1 3)   Gerade h: x=q+t*v
         TTMathe:
g=p+s*u h=q+t*v mit GH senkrecht g und senkrecht h führt auf LGS
1*s-5*t=-3 10*s-1*t=19 s=1 t=2 G(7|11|-2) H(1|-1|2)
Abstand d(g,h)=g(G,H)=14 Winkel zwischen u und v phi=8,1301023542°

(Ebene Geometrie ist ein eigenständiges Programm. Siehe TTGEO )

Strecke, Dreieck, Kreis, Gerade, Ebene, Kugel im Raum veranschaulichen.
Lösung der quadratische Gleichung wird vorgerechnet.
Losung der Gleichung 3. und 4. Grades wird vorgerechnet. Cardano
Lösung beliebiger Gleichungen kann über Schaubild ermittelt werden.
Polymommultiplikation und -Division Beispiele

Kettenbrüche. Zum Beispiel:

  sqrt(2) = [1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...]
  sqrt(3) = [1,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,...]
                    und umgekehrt
  [0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...] = (sqrt(5)-1)/2
  [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...] = (1+sqrt(5))/2

Lissajoufiguren

Die Bahn wird nach folgender Formel berechnet.: x(t) = sin(a*t + b); y(t) = sin(c*t + d)
Das Frequenzverhältnis entspricht dabei a:c,
die Phasenverschiebung den Parametern b und d.

Weitere Beispiele mit TTGeo gezeichnet
Siehe Programmierung