Umwandlung einer Dezimalzahl in eine Binärzahl
Hinweis: Lektion 15 bis 19 werden für Lektion 20ff nicht vorausgesetzt.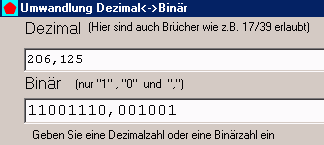
Downloadseite
"Umwandlungg Dezimalzahl in Binärzahl" (dez_bin.exe)
"Umwandlung Dezimalzahl in Hexadezimalzahl etc" (dez_in_b.exe)
Der Algorithmus ist ganz einfach. Er werde an einem Beispiel
erläutert.
Die Umwandlung ins 3-System oder ins System mit der Basis B
erfolgt analog. Im 3-Sytem ist a mod 3 eine Ziffer aus
{0;1;2} im B-System ist a mod B eine Ziffer aus {0;1; ... ;
B-1}.
Beispiel: 99810 = 11111001102 bedeutet:
998 im Zehnersystem = 1111100110 im Zweiersystem
denn: 998=1·29+1·28+1·27+1·26 +1·25+0·24+0·23+1·22+1·2+0·2
I Umwandlung einer natürlichen Zahl (Vorkomma)
Sei n=99810=a9a8a7a6a5a4a3a2a1a02 =a9·29+a8·28+...+a2·22+a1·2+a0Dabei handelt es sich um die Zahl 998 im Dezimalsystem und ihre Ziffern a9,a8, .... a0 im Dualsystem.
Beachte: a0 ist 1, wenn die Zahl ungerade, sonst Null und n dividiert durch 2=a9a8...a1 Rest a0.
In Pascal: n mod 2 = a0
n1=n div 2 =a9a8...a1 (Verschiebung um 1)
Jetzt wiederholt sich das ganze:
n1 mod 2 = a1
n2=n2 div 2 = a9a8...a2
....
Im Beispiel: 99810=11111001102, denn
998 div 2 = 499 Rest 0 letzte Dualziffer
499 div 2 = 249 Rest 1 vorletzte Dualziffer
249 div 2 = 124 Rest 1 ...
124 div 2 = 62 Rest 0
62 div 2 = 31 Rest 0
31 div 2 = 15 Rest 1
15 div 2 = 7 Rest 1 ...
7 div 2 = 3 Rest 1 dritte Dualzifer
3 div 2 = 1 Rest 1 zweite Dualziffer
1 div 2 = 0 Rest 1 erste Dualziffer
Somit erhält man durch folgende Prozedur die Dualdarstellung:
function DezInBinVorkomma(n: integer):string;
begin
result:='';
repeat
if n mod 2 =0 then result:='0'+result
else result:='1'+result;
n:=n div 2;
until n=0;
end;
(Im Programm ist noch die Vorgabe, dass n in einem String gegeben ist).
II Umwandlung einer Dezimalzahl (Nachkommastellen)
Sei n=0,8210=0,a1a2a3a4...2= a-1·2-1+a-2·2-3+a-3·2-6+...Dabei handelt es sich um die Zahl 0,82 im Dezimalsystem und ihre Ziffern a0,a1,a2,... im Dualsystem.
n, der Reihe nach mit 2 multipliziert, ergibt als Vorkommastelle zuerst a0, dann a1, ...
Im Beispiel ist 0,82(10) =0.11010001111010111000... (2), denn
0,82·2 = 1,64 => 1. Dualziffer nach dem Punkt ist 1
-
0,64·2 = 1,28 ==> 2. Dualziffer nach dem Punkt ist 1
-
0,28·2 = 0,56 ==> 3. Dualziffer nach dem Punkt ist 0
-
0,56·2 = 1,12 ==> 4. Dualziffer nach dem Punkt ist 1
-
...
Somit erhält man durch folgende Prozedur die Dualdarstellung:
function DezInBinnachkomma(r: real):string;
var n: integer;
begin
result := '0.';
n := 0;
repeat
inc(n);
r := 2*r;
if r >= 1 then Begin
result:=result + '1';
r:= r - 1;
End else result := result + '0';
until (r = 0) or (n > 64);
end;
November 2002: Philipps Verbesserungsvorschlag:
function DezInBinnachkomma(r: real):string;
begin
result := '0.';
repeat
r := 2*r;
if r >= 1 then Begin
result := result + '1';
r := r-1;
End else result:= result + '0';
until r < 1E-20;
end;
Zwei Vorteile: 1. Zählvariable n entfällt.
2. Viel stichhaltiger: Bei der ersten Version wird r = 0 geprüft. Sowas wird unter Informatikern bei r real wegen der Rundungsfehler als Programmierfehler betrachtet.
Nebenbei bemerkt: Nur Brüche mit einer Zweierpotenz im Nenner sind im Dualsystem endlich. Alle anderen unendlich z.B.
0,1 10) = 0.0001100110011001100110011...2) Im Computer nur ... 0,9 10 = 0.1110011001100110011001100...2 ... endlich ... 0,1+0,9 = 0,1111111111111111111111111...(2) ... viele Stellend.h. ein Programmierer, der in einer Schleife mit Anfangswert 0 und der Schrittweite 0,1 abfragt, wann 1 erreicht ist, erleidet damit Schiffbruch! Statt 1 wird möglicherweise nur 0,111..12=0,999...9(10) erreicht!
Das Programm bleibt bei einer wichtigen Anwendung "hängen". Schleifenende wird nicht ereicht: Programm ist unbrauchbar! Kunde ist verärgert! Keine weiteren Aufträge!
- Als Programmierer muss man stets Murphy's Gesetze beachten:
- 1. Gesetz: Wenn etwas schiefgehen kann, dann wird es auch schiefgehen.
- ...
- 246. Gesetz ((c) J. Mohr) Wenn etwas schiefgehen kann aber nicht schiefgehen muss, dann geht es beim Testen nicht schief, aber garantiert im Ernstfall.
Ich hatte ein Programm geschrieben (ca. 1979), das
die Daten unserer Abiturienten erfasst,
Belegüberprüfungen und Berechnungen durchführt
und zum Schluss das komplizierte Abiturzeugnis ausdruckt. Das
Programm funktionierte jahrelang einwandfrei. Doch
plötzlich erhielten Schüler ein "befriedigend", wo
eigentlich hätte "gut" stehen müssen.
Was war passiert? Ich hatte den Compilerschalter von Pascal auf
"doppelte Rechengenauigkeit" gestellt. Mehr nicht.
Die Auswirkung war vereinfacht folgende:
Beim Punkteschema entspricht 7, 8 und 9 Punkte "befriedigend",
10, 11 und 12 Punkte "gut".
Bei mehreren Noten wird der Mittelwert gebildet. Dabei wird ab
n=9,5 auf "gut" aufgerundet (Achtung: unstetige
Funktion!).
Beim Umstellen des Compilers war (vereinfacht ausgedrückt)
der Mittelwert nicht mehr n=9,5 sondern n=9,499999999999999999 und die Abfrage
...
if n < 9,5 then s := "befriedigend" else s := "gut"
...
führte nach der Umstellung des Compilerschalters zu dem
fatalen Ergebnis.
|
Literatur: Zu dieser Problematik ist folgender Aufsatz zu
empfehlen: "What every computer scientist should know about floating-point arithmetic". Siehe http://www.validlab.com |
Aufgabe 17.1:
Das nebenstehende (fehlerhafte) Programm soll von der Dezimalzahl n, die in Edit1 steht, die zugehörige Dualzahl berechnen.
a) Gib die Dualdarstellung der Zahl 206 an!
b) Was berechnet das Pragramm stattdessen bei der Eingabe von n=206?
c) Wie müsste man das Programm ändern, dass die Umwandlung bei Eingabe von n=206 richtig erfolgt? (wenig!)
d) Was würdest Du bei diesem Programm noch beanstanden?
procedure TForm1.Button1Click(Sender: TObject);
var n,p,i: integer;
s: string;
begin
n := strToInt(edit1.text);
p := 128;
s := '';
for i := 1 to 8 do Begin
if n >= p then BEgin
n := n - p;
s := s + '1';
ENd else s := '0' + s;
p := p div 2;
ENd;
showmessage(s);
end;
Lösung
III Umwandlung eine Binärzahl in eine Dezimalzahl
Beispiel Vorkomma: n=101011(2)=1*1+1*2+0*4+1*8+0·16+1*32 = 43 (10) Beispiel Nachkomma: n=0,1001(2)=1*1/2+0*1/4+0*1/8+1·1/16 = 0,5625 (10)
Die Prozeduren sind elementar und wohl ohne große Erläuterung verständlich.
function BinInDezVorkomma(s:string;
var r:extended):boolean;
var k:integer;
p:extended;
begin
trim(s);
r:=0;
p:=1;
for k:=length(s) downto 1 do Begin
if s[k]='1' then r:=r+p else
if s[k]<$gt;'0' then BEgin
//Binärzahl nur 1 und 0 erlaubt
result:=false;
exit;
ENd;
p:=p*2;
End;
result:=true;
end;
function BinInDezNachkomma(s:string;
var r:extended):boolean;
//true kein Fehler
var k:integer;
p:extended;
begin
trim(s);
r:=0;
p:=1/2;
for k:=1 to length(s) do Begin
if s[k]='1' then r:=r+p else
if s[k]<>'0' then BEgin
//Binärzahl nur 1 und 0 erlaubt
result:=false;
exit;
ENd;
p:=p/2;
End;
result:=true;
end;
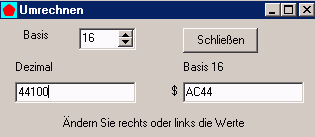
DownloadseiteIV Umwandlung Dezimalzahl in Hexadezimalzahl (oder beliebige Basis) und umgekehrt
Die Oberfäche dieses Programm findest Du oben rechts.
function copyab(const s:string; const i:integer):string;
//Rest von s ab i. em Zeichen
begin result:=copy(s,i,length(s)-i+1) end;
function BinInDezVorkomma(s:string;
var r:extended):boolean;
var k:integer;
p:extended;
begin
trim(s);
r:=0;
p:=1;
for k:=length(s) downto 1 do
Begin
if s[k]='1' then r:=r+p else
if s[k]<>'0' then BEgin
result:=false;
exit;
ENd;
p:=p*2;
End;
result:=true;
end;
function BinInDezNachkomma(s:string;
var r:extended):boolean;
//true kein Fehler
var k:integer;
p:extended;
begin
trim(s);
r:=0;
p:=1/2;
for k:=1 to length(s) do Begin
if s[k]='1' then r:=r+p else
if s[k]<>'0' then BEgin
result:=false;
exit;
ENd;
p:=p/2;
End;
result:=true;
end;
function BinInDez(s:string):string;
var n:integer;
a,b:string;
vork,nachk:extended;
korrekt:boolean;
begin
n:=pos('.',s);
if n=0 then n:=pos(',',s);
if n=0 then Begin
korrekt := BinInDezVorkomma(s,vork);
if korrekt then result := floatToStr(vork)
else result := 'Falsche Eingabe';
End else Begin
a:=copy(s,1,n-1);
b:=copyab(s,n+1);
korrekt:=BinInDezVorkomma(a,vork) and
BinInDezNachkomma(b,nachk);
if korrekt then result:=floatToStr(vork+nachk)
else result:='';
End;
end;
function DezInBinVorkomma(s:string):string;
var n:integer;
begin
result:='';
try n:=StrToInt(s) Except result:=''; exit End;
repeat
if n mod 2 =0 then result:='0'+result
else result:='1'+result;
n:=n div 2;
until n=0;
end;
function DezInBinnachkomma(s:string):string;
var r:extended;
n:integer;
begin
r:=StrToFloat('0'+Decimalseparator+s);
result:='';
n:=0;
repeat
inc(n);
r:=2*r;
if r>=1 then Begin
result:=result+'1';
r:=r-1;
End else result:=result+'0';
until (r=0) or (n>64);
end;
function DezInBin(s:string):string;
var n:integer;
a,b:string;
begin
n:=pos('/',s);
if n>0 then Begin //Bruch->Dezimalzahl
a:=copy(s,1,n-1);
b:=copyab(s,n+1);
try s:=FloatToStr(strToFloat(a)/StrToFloat(b));
except result:='Falsche Eingabe' End;
End;
n:=pos('.',s);
if n=0 then n:=pos(',',s);
if n=0 then result:=DezInBinVorkomma(s) else Begin
a:=copy(s,1,n-1);
b:=copyab(s,n+1);
result:=DezInBinVorkomma(a)
+decimalseparator+DezInBinNachkomma(b);
End;
end;
procedure TForm1.E_dezChange(Sender: TObject);
begin
if e_bin.focused then exit;
try
e_bin.text:=dezInBin(e_dez.text);
except e_bin.text := 'Falsche Eingabe' End;
end;
procedure TForm1.E_binChange(Sender: TObject);
begin
if e_dez.focused then exit;
try
e_dez.text:=BinInDez(e_bin.text);
except e_dez.Text := 'Falsche Eingabe' End
end;
In Simon Reinhards www.delphi-fundgrube.de ist folgende allgemeine Routine angegeben:
(Nur noch im Archiv aufrufbar:Archiv)
type
TNumbBase = 1..36;
function NumbToStr(Numb: LongInt; Base: TNumbBase): String;
const NumbDigits = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ';
begin
Result:=EmptyStr;
while Numb > 0 do begin
Result:=NumbDigits[(Numb mod Base)+1]+Result;
Numb:=Numb div Base;
end;
if Result=EmptyStr then
Result:='0';
end;
Umwandlung eines Dezimalbruches in einen möglichst einfachenBruch
Problemstellung: Sie wollen eine einfache Bruchrechnung in Ihr Programm implementieren:Umwandlung eines Bruches in den Typ Real ist kein Problem.
Zum Beispiel:
1/2 -> 0.5
1/3 -> 0.33333...3 (Genauigkeit je nach Compiler)
Jetzt führen Sie einige Rechenoperationen aus:
Zum Beispiel die Summe von 1/2 und 1/3:
0.5 + 0.33333...3 = 0.83333...3
Wie erhalte ich nun aus 0.83333...3 den exakten Bruch 5/6?
