Joachim Mohr   Mathematik Musik
≡

Delphi-Kurs

Lektionen in Delphi

Für blutige Anfänger ist die erste Einführung gedacht.
Technische Hinweise
Inzwischen (Stand: Mai 2015/März 2020) ist die Entwicklungsumgebung von Free-Pascal (eine kostenlose Version) zu neuem Leben erwacht und kann unter den Namen Lazarus heruntergeladen werden. Meine neueren Programme entwickle ich zur Zeit unter dieser Umgebung weiter und kann sie deshalb mit gutem Gewissen weiterempfehlen.
Alle Lektionen der Delphi-Ecke sind in der gepackten Zip-Datei Delphi-Ecke (Stand: 12.02.2007 mit ca. 3 MB enthalten und können lokal auf den Computer heruntergeladen werden.

Die Lektionen

M­oti­va­tion Wozu über­haupt Program­mieren lernen?
1. Lektion Das erste Programm "Hallo Welt"
2. Lektion Variablen und Wer­tzu­weisung
3. Lektion if ... then ... else I. Teil
4. Lektion
  		Schleife: for .. to .. do ..Begin .. End
Summen und Produkte
5. Lektion
  		repeat und while-Schleifen
Werte­tafeln
... zu­sammen­fassen­de Auf­gab­en
wei­tere Auf­gaben
6. Lektion Pasca­lfunktionen (Einstieg)
7. Lektion if .. then .. else II.Teil
div und mod
Prim­zahlen und Prim­faktoren
8. Lektion Case .. of .. End
zu­sammen­fassende Auf­gaben
9. Lektion Algorithmen
Der eu­kli­dische Al­go­rith­mus
10. Lektion Re­kur­sive Funk­tio­nen I. Teil: Er­ste Bei­spie­le
11. Lektion Pro­zedur­en
12. Lektion Itera­tionen
zu­sammen­fassende Aufgaben
13. Lektion Re­kur­sion II. Teil: Basis­wissen
14. Lektion Arrays und Ordnung­salgorith­men
zusammen­fassende Aufgaben
Die 15. Lektion wird für Lektion 16 u.s.w. nicht voraus­gesetzt.
15. Lektion Das Gauß-Verfahren zur Lösung eines LGS
16. Lektion Recordtypen
17. Lektion Ein zweites Fenster erzeugen
18. Lektion Objekt­orientierte Program­mierung:
Unter­schied zwischen Pro­zedur und Me­thode
  19. und 20. Lektion für Er­gän­zungen noch freigehalten
21. Lektion Eigen­schaften, Me­thoden und Ereig­nisse am Bei­spiel Öff­nen und Spei­chern von Da­teien
22. Lektion Klassen und Instanzen
23. Lektion Klas­sen selbst de­finieren
24. Lektion Nach­komme von TForm selbst schreiben
Anhang 1 hoch(x,n) = xn für x,n: real
Anhang 2 Genauigkeit bei der Gleit­komma­rechnung
Anhang 3 Ein Programmmanager. (Deine eigene Start­leiste)
Anhang 4 Lektion in Graphik
Anhang 5 Lektion in Bild­bearbeitung
Anhang 6 Bewegung aufs Bild: Ver­wen­dung der Timer­komponente
Anhang 7 Wettrennen: Images werden zur Lauf­zeit erzeugt und mit Bild ge­laden
Anhang 8 Wie Delphi definieren wir selbst eine Form als Klasse.
Anhang 9 Rekursion III. Teil: Ein mathe­matischer Parser
Anhang 10 Um­wand­lung von Dezimal­zahlen in Dual­zahlen
Anhang 11 Kryptologie
Anhang 12 Vermischtes (Die FAQ)
Bemerkungen zu diesen Lektionen:

Mathematisch wird der Anfangskenntnisstand der Oberstufe des Gymnasiums vorausgesetzt.

Dieser Delphikurs soll nicht Windows erklären, sondern in die grundlegenden Praktiken einführen, die jeder Programmierer kennen sollte - gleichgültig in welcher Programmiersprache er zu schreiben gedenkt.

An praktischen Beispielen soll der Anfänger als Bestandteile algorithmischer Problemlösungen kennen lernen:

1. Eingabe und Ausgabe 2. Va­riablen­typ 3. Wert­zu­weisung 4. Wie­der­h­lung
5. Verzweigung 6. Funk­tion 7. Pr­zedur 8. Al­g­rith­mus
9. Iteration 10. Re­kur­sion 11. Array (Vektor) 12. Record (Datenblatt)
13. Genauigkeit bei Real 14. Klas­se In­stanz 15. Eigen­s­chaft Me­thode 16. etwas OOP
17. Daten speichern 18. Ver­zeich­nisse lesen 19. Gra­phik 20. Bild­bearbei­tung

Das sind für Anfänger viele verwirrende Elemente. Sie gibt es aber in jeder guten Programmiersprache. Um damit umgehen zu können, muss man lernen, sich vorzustellen, was im Computer passiert, wenn der Programmcode ausgeführt wird.

Das ist ein langwieriger Lernprozess. Als Anfänger muss man daher viel üben. Diese Lektionen werden Dir dabei helfen. Die ersten Lektionen sind dabei die wichtigsten.

Delphi zwingt wie die Vorgängersprache Pascal zum logischen und strukturiertem Aufbau eines Programms. Die Deklaration aller verwendeten Variablen ermöglicht einen Überblick über ihren Gültigkeitsbereich.

Mit diesem Grundwissen kann sich dann der fortgeschrittene Programmierer anwendungsorientierten Projekten widmen.
Einfache und komplexe Beispiele findest du hier in der Delphi-Ecke.

Eine kurze Bemerkung zu Delphi:

Delphi ist ein sogenanntes schnelles Entwicklerwerkzeug (Rapid Application Development Tool). Das Schreiben von Quelltext wird drastisch reduziert, da du die Standardwindowselemente wie Meldungs-, Eingabe-, Pfadsuchfenster u.s.w. mit ein paar Mausklicks verfügbar machen kannst. Die Fehlersuche beschränkt sich auf Deinen Quelltext, da die Windowselemente dank ihrer gekapselten Eigenschaften und Funktionen einwandfrei funktionieren und von dir auch nicht durch Nebeneffekte gestört werden können.

Noch ein Hinweis (jetzt vielleicht noch unverständlich):

Einstellungen, die du sinnvollerweise zur Entwurfszeit im Objektinspektor vornimmst, werden in Beschreibungen oft als Laufzeitzuweisungen angegeben. Wenn du diese Zeilen in dein Programm mitkopiert, kann du dir die Einstellungen im Objektinspektor sparen. (Du sollst jedoch die Alternative kennen und anwenden können!)
Zum Beispiel:
  memo1.Font.Name := 'Courier New'; //Im Objektinspektor
  memo1.Font.Size := 12;      //Im Objektinspektor
Motivation: Wozu überhaupt programmieren lernen? nach M. Papst, Plauen

Braucht man das später wirklich? Man kann doch noch vieles mehr mit dem Computer machen ohne ihn zu programmieren? Alle bedienen doch so den Computer - beruflich und privat? Und Geldverdienen als Lieferant kommerzieller Software kommt für mich sowieso nicht in Frage!

Aber es ist eine gewaltiger Unterschied, ob man einen Computer bedient oder beherrscht:

"Bedienen" des Computers ist schnell gelernt, weil es von "Dienen" kommt. Wie oft ärgert man sich über den Computer, weil er es anders machen zu müssen glaubt, als dem Bediener vorschwebt. Man muss die Bedienungsanleitung genau kennen, um im richtigen Augenblick einen Mausklick hier, einen anderen Mausklick dort und so weiter zu machen. Und wenn nichts mehr geht, wird einem schon die Hotline weiterhelfen. Die kennt schließlich schon die gröbsten Programmierfehler und wie man ihnen ausweicht.

Ist es nicht besser, diese Technik zu beherrschen als ihr nur zu dienen?

Mit Hilfe des Computers wollen wir ja unsere Arbeit erleichtern und nicht erschweren.

Und dazu ist ein Grundverständnis von Programmabläufen unentbehrlich.

Man muss wissen:
Wie kann ich das Problem analysieren?
Wie ist es strukturiert?
Wie plane ich vorausschauend am besten?
Wie kann ich Aktivitäten verteilen und verknüpfen?
Gibt es Alternativen?
Kurz: Wie denke ich algorithmisch?
Und ist es im Alltagsleben - beruflich oder privat- nicht genauso?

Als Vorgesetzter ist es zwingend erforderlich, richtig planen zu können. Und eine gute ChefIn wird MitarbeiterInnen, die mitdenken, die Anerkennung nicht verweigern.

Auch hier wird uns eine intensive Schulung im algorithmischen Denken von Vorteil sein!

Mit dieser Bildung werden wir komplizierten Situationen immer besser gewachsen sein!

Und wie ist es, wenn Du nur Programme einsetzt oder sogar Programme erstellen lässt?

Wenn Du etwas vom Programmieren verstehst, weißt Du viel besser, was Du von einem Programm verlangen kannst und was nicht. Du kannst viel besser beurteilen, ob die Softwarefirma was taugt oder ob das Geld für teure Programme schlecht angelegt ist.

Schließlich werden beim Programmieren von herausfordernden Problemen unterhaltsame und kreative Kräfte freigelegt.

Das kann ungeheuren Spaß machen!

Technische Hinweise

Alle Lektionen und Texte der Delphi-Ecke sind in der gepackten Zip-Datei Delphi-Ecke (ohne Urlaubsbilder) (Stand: 12.02.2007 mit ca. 3 MB) enthalten und können lokal auf den Computer heruntergeladen werden.

Für blutige Anfänger ist die erste Einführung gedacht.
Eine günstige Einsteigerversion (immer noch brauchbar Delphi 4) gibt es auf CD im Buch "Delphi für Kids" (ca. 19 €).

Herr Volker Tautz teilte mir freundlicherweise folgendes mit:
In der neueren Ausgabe "Delphi für Kids" von Hans-Georg Schumann von Mitp-Verlag (Taschenbuch - August 2005) (24,95 €) ISBN 978-3-8266-1529-0 liegt eine CD mit einem voll funktionsfäheigen Delphi 7 bei.

Im Buch wird auf Seite 407ff. die Installation genau beschrieben: Von CodeGear from Delphi erhält man von einen Schlüssel, mit dem man Delphi 7 installieren kann (unter Vista muss das setup.exe mit der rechten Maustaste "Als Administrator ausführen" gestartet werden.). Wer die manchmal nützliche Hilfe-Datei "WinHlp32.exe" benutzen will, muß diese sich diese von Microsoft herunterladen.)
Neu: Interessant ist auch die 2007-Ausgabe von Turbo-Explorer von Borland Software Corporation

1. Lektion: Das erste Programm "Hallo Welt"

Dazu:
Programm Abspeichern
Auf Diskette kopieren
Objekt, Eigenschaft, Methode
Kommentare nach "//" und zwischen geschweifte Klammern

Beispiel 1.1:

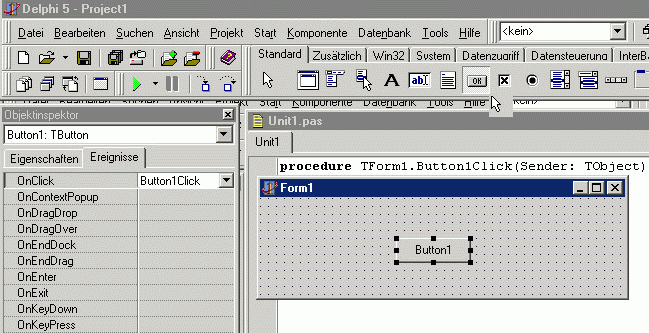
1delphi_bsp1.gif 
  Starte in Delphi eine Neue Anwendung (Menu Datei|Neu).
  Klicke in der Komponentenleiste auf einen Button und setze ihn
  aufs Formular und klicke im Objektinspektor auf das
  Ereignis OnClick.
  Delphi schreibt folgenden Quellcode:

procedure TForm1.Button1Click(Sender: TObject);
begin

end;

 Merke: Was Delphi schreibt, darf nicht geändert oder
     gelöscht werden! Du darfst nur vor begin die
     Variablen deklarieren (siehe Programme in Lektion 1)
     und zwischen begin und end Deine Anweisungen.
 Ergänze nun die Prozedur folgendermaßen:

procedure TForm1.Button1Click(Sender: TObject);
begin
 ShowMessage('Hallo Welt'); //Einzige Anweisung
end;
Hinweis:
Kommentare kann man nach // schreiben, zwischen { und } oder zwischen (* und *).
Kommentare überliest der Compiler und werden nur zur Programmerklärung verwendet.

Speichere mit Menü Datei|Projekt speichern unter... in einem Eigenen Ordner HalloWelt ab.

Delphi speichert zu jedem Projekt mehrere Dateien ab, nämlich .RES (Ressourcendatei) .DPR (Projektdatei) .DFM (graphische Formulardatei) werden alle von Delphi verwaltet und .PAS (Unit Quelltext, nur in diesem schreibt der Programmierer)

Jetzt Programm starten:

Der Compiler erzeugt Unit-Object-Zwischencode .DCU und die eigentliche ausführbare Datei .EXE (nur die erhält der Kunde).

Hinweis:
Wenn Du Dein Programm auf Diskette schreibst, kopiere nur die .RES-, die .DPR-, die .DFM- und die .PAS- Dateien. (die .DCU- und die .EXE- erfordern ca. 10 mal so viel Speicherplatz)

Du erkennst hier:
Die Programmentwicklung in Delphi verläuft in drei Etappen:
1. Etappe:
Bedieneroberfläche gestalten. Hier: Das Objekt button1, d.h. eine Instanz von Tbutton, platzieren

2. Etappe:
Objekteigenschaften zuweisen. Hier: Im Objektinspekor button1 zum Beispiel die captionOKgeben. Denkbar ist auch die Schrift (Font) zu vergrößern.

3. Etappe:
Ereignisbehandlung schreiben. Hier SchowMessage(..). Zwischen Groß- und Kleinschreibung wird nicht unterschieden. Du kannst auch showmessage schreiben.
Bald werden dir folgende Bezeichnungen geläufig werden:

Objekte.
Zum Beispiel der "OK-Knopf" als button1. Man sagt auch: Das Objekt button1 ist eine Instanz des Objekttyps Tbutton. Bei Delphi heißen die sichtbar gemachten Objekte Komponenten.

*) Objekte haben Eigenschaften (z.B. caption oder left)
*) Objekte reagieren auf Ereignisse (z.B. Mausklick)
*) Objekte haben Methoden = spezielle Prozeduren. Zum Beispiel show und hide.


Man spricht hierbei von Objektorientierter Programmierung (OOP).
niklaus wirth
Niklaus Wirth, geboren 1934 Winterthur, Schweiz

Das von Borland/Inprise entwickelte Delphi ist eine objektorientierte Nachfolgesprache von Pascal, einer von dem Zürcher Professor Niklaus Wirth entwickelte klar konzipierte und streng strukturierte Programmiersprache, benannt nach dem französischen Philosophen und Mathematiker Blaise Pascal (1623-1662), der um 1640 (vor seiner mystischen Erleuchtung) eine mechanische Rechenmaschine entwickelt hatte.

Die von ihm inspirierte objektorientierte Nachfolgesprache Oberon setzte sich leider nicht durch, obwohl sie gegenüber Delphi oder auch Java den außerordentlichen Vorteil hat, kurz und bündiges Programmieren zu verlangen. Siehe "Pascal and its Successors"(25.09.2002) von Niklaus Wirth. (Zitat: Are we therefore condemned to eternally produce an ever growing mountain of software of ever growing complexity, software that nobody fully understands, although everybody is well aware of its defects and deficiencies?")

Im folgenden ist häufig von Pascal die Rede. Damit ist Quelltext von Delphi gemeint, der reines bewährten Pascal ohne OOP darstellt.


Beispiel 1.2:
Lasse Dich nicht von den vielen Fachausdrücken verwirren. Du sollst sie hier nur einmal gehört haben. Eigentlich wichtig werden sie erst ab Lektion 20. Das Lernziel hast Du erreicht, wenn Du weißt, was im Programm geschieht.

1. Etappe:
Setze zwei Instanzen button1 und button2 von dem Objekttyp Tbutton und eine Instanz label1 von dem Objekttyp Tlabel auf die Instanz form1 vom Objekttyp TFormular.
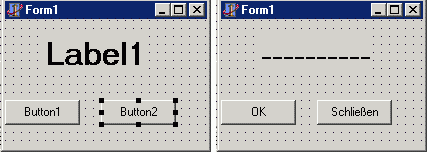
1delphi_bsp2_1.gif
Bemerkung: Die Instanz form1 vom Typ TForm1 ist automatisch vorhanden, wenn du eine neue Anwendung startest.

2. Etappe:


3. Etappe:
Jetzt wird der eigentliche Quellcode geschrieben:
Die Methode für das Ereignis Klicken-auf-Button1.
Das hört sich komplizierter an, als es ist. (Ab Lektion 20 beschäftigen wir uns damit ausführlicher.) Dein Quelltext sieht folgendermaßen aus:

procedure TForm1.Button1Click(Sender: TObject);
begin
 label1.Caption := 'Hallo Welt';
 label1.Show;
 button1.hide;
 button2.show;
 button2.left := button1.left;
end;
Klicke Schließen an und wähle im Objektinspektor das Ereignis OnClick. Und ergänze den Quelltext folgendermaßen: 


procedure TForm1.Button2Click(Sender: TObject);
begin
 close
end;
close bezieht sich hier auf form1, da hier Button2Click eine Methode von Tform1 ist.

Der Befehl close schließt das Hauptfenster form1 und damit die gesamte Anwendung: Das kurze Leben von "Hallo Welt" ist beendet.

Starte nun dein Programm. Du siehst: Dem Anwender bleibt nichts anderes übrig, als zuerst den OK-Knopf und dann den Schließen-Knopf zu betätigen. Das nennt man intuitive Benutzerführung.

2. Lektion: Variablen

Dazu:
Wertezuweisung "a := ..."
+ beim Typ string
Die Pascal-Funktionen: showmessage, IntToStr und floatToStr

Mit Hilfe der Variablen werden Werte im Computer gespeichert.

Variablentypen:

integer ganze Zahlen Z={...-3, -2, -1, 0, 1, 2, 3,...}
real reelle Zahlen. Genauer: Gleitkommazahlen (floating point numbers)
strings Zeichenketten (der Form 'xyz')
boolean Wahrheitswerte (true und false)
Hinweis: Computer haben nur endlichen Speicher.
Deshalb sind bei Delphi Integer-Zahlen n zur Zeit auf den Bereich |n| 〈 231 und Real-Zahlen auf 15 bis 16 signifikante Stellen beschränkt.
Wenn man konkrete Aufgaben löst, gibt man bei Gleitkommazahlen vor, mit welcher Genauigkeit gerechnet werden soll. Statt Real ist möglich: single Einfache Genauigkeit, weniger Platzbedarf, schnelleres Rechnen. double Doppelte Genauigkeit, mehr Platzbedarf, je nach Prozessor langsameres Rechnen.
In Delphi 2 bis Delphi 8 ist der Typ "Real" als "Double" implementiert. 
Übung: Welche Werte stehen in den folgenden Programmen in
    den für die Variablen reservierten Speicherbereichen?
    Schreibe dies Zeile für Zeile auf!

Aufgabe 2.1: Protokolliere die Variablenbelegung!
  a) Füge nach jedem Befehl ein:
    showmessage('a=' + a);
    (Ersetzte gegebenenfalls passend a durch b und c!)

procedure TForm1.Button1Click(Sender: TObject);
 var a, b, c:string;
begin
 a := 'Hallo';
 b := 'Welt';
 c := a + ' ' + b;
end;

Hinweis: Jeder Befehl wird mit einem Semikolon abgeschlossen!

Praktischer Hinweis:
Du kannst diese Prozedur in ein Delphiproject kopieren. Dazu musst Du einen button1 auf dem Formular platzieren und auf ihn doppelklicken: Lösche dann das Gerüst procedure ... end; und kopiere die hier geschriebene Prozedur in Deine Unit. (So ersparen wir uns die Arbeit, jeweils das ganze Project in einem eigenen Ordner zu kopieren. Außerdem sind die Lektionen ohne unzählige Projectordner viel übersichtlicher.).
>
  b) Füge nach jedem Befehl ein!
   showmessage('a=' + IntToStr(a) + ' b=' + IntToStr(b) +
         ' c=' + IntToStr(c));

procedure TForm1.Button1Click(Sender: TObject);
 var a, b, c: Integer;
begin
 a := 5; b := 7; c := 9;
 a := b; b := c; c := a;
 a := a + 1; b := b-1; c := c-1;
end;

  c) Füge nach jedem Befehl ein!
   showmessage('a=' + floatToStr(a) + ' b=' + floatToStr(b));
   Ersetzte gegebenenfalls passend a und b durch c und d!

procedure TForm1.Button1Click(Sender: TObject);
 var a,b,c,d:real;
begin
 a: = 1 + 3/10; b := - 3/10;
 a: = a + 1/10; b := b - 1/10;
 c: = a + b; d := 1 - c;
end;

 d) Füge nach jedem Befehl ein: showmessage(...)
procedure TForm1.Button1Click(Sender: TObject);
  var a,b,c:integer;
begin
 a := -7; b := 11; c := 13;
 a := a + 6; b := b-12; c := c-11;
 a := a + b; b := b + c; c := a + b;
 a := a + b + c; b := a + b + c; c := a + b + c;
end.

 e) Was berechnet folgendes Programm?
  (Schreibe keine Zahl sondern einen Rechenausdruck!)

procedure TForm1.Button1Click(Sender: TObject);
  var s:real;
begin
 s := 0;
 s := s + 1;
 s := s - 1/3;
 s := s + 1/5;
 s := s - 1/7;
 s := s + 1/9;
 s := s - 1/11;
 //weiter siehe Aufg. 4.2
end;

Lösung

3. Lektion: if .. then und if .. then .. else .. I. Teil

Dazu: random(n)

Wir können Bedingungen mit if.. then .. in unser Programm einbauen: Ein Befehl wird nur ausgeführt, wenn eine Bedingung erfüllt ist. 


Beispiel 3.1: Eine Zufallszahl wird mit Worten ausgegeben:

procedure TForm1.Button1Click(Sender: TObject);
 var k:integer;
begin
 k := random(2) + 1; // k = 1 oder k = 2
 if k = 1 then showmessage('Eins');
 if k = 2 then showmessage('Zwei');
end;
Bemerkung:
random(n) liefert eine Zufallszahl x mit 0 〈= x 〈 n. Vor dem ersten Aufruf sollte randomize aufgerufen werden. Dabei wird der globalen Variablen RandSeed einen von der Systemzeit abhängigen Anfangswert zugewiesen.


Deshalb sollte bei bei wichtigen Anwendungen wie Simulationen folgendes eingefügt werden.

procedure TForm1.FormCreate(Sender: TObject);
begin
Randomize;
end;


Dann erhält der Anwender garantiert bei jedem Start ein neues Ergebnis.
Zum Testen kann man statt randomize zum Beispiel RandSeed := 0 setzten. Dann erhält man immer dieselbe Folge von "Zufalls"-zahlen.
Beispiel zu if Ausdruck then Anweisung1 else Anweisung2. Wenn der Ausdruck True ergibt, wird Anweisung1 ausgeführt, andernfalls Anweisung2.
Beispiel 3.2: Dasselbe wie in Beispiel 3.1 wird mit folgendem Programm erreicht: 
procedure TForm1.Button1Click(Sender: TObject);
 var k:integer;
begin
 k := random(2) + 1;
 if k = 1 then showmessage('Eins') else
  showmessage('Zwei');
end;

Aufgabe 3.1:
Eine Aussage über zwei ganze Zahlen wird gemacht. Verwende dazu aus der Komponentenpalette "Beispiele" zwei Spinedits. Mit diesen kann man ganze Zahlen mit der Eigenschaft value auslesen.

Was ist der Unterschied von a) und b) 
a)Beachte ...
procedure TForm1.Button1Click(Sender: TObject);
 var a,b:integer;
begin
 a := spinedit1.Value;
 b := spinedit2.Value;
 if a 〈 b then 
  showmessage('Erste Zahl kleiner als 2. Zahl');
 if 2*a 〈 b then 
  showmessage('Erste Zahl kleiner als die Hälfte der 2. Zahl');
end;

b)1
procedure TForm1.Button1Click(Sender: TObject);
 var a,b:integer;
begin
 a := spinedit1.Value;
 b := spinedit2.Value;
 if 2*a 〈 b then 
  showmessage('Erste Zahl kleiner als die Hälfte der 2. Zahl') else
 if a 〈 b then 
  showmessage('Erste Zahl kleiner als 2. Zahl');
end;

Lösung

Beispiel 3.4: Kopfrechenübung: Zwei Zufallszahlen x,y
       mit 0 〈= x,y 〈= 10 sollen durcheinander dividiert werden.

procedure TForm1.Button1Click(Sender: TObject);
 var x,y:integer;
begin
 randomize;
 x := random(11); //liefert Zufallszahl aus {0,1,...,10}
 y := random(11);
 showmessage('Schätze ' + intToStr(x) + '/' + intToStr(y) + '!');
  if y = 0 then showmessage('Durch 0 darf nicht dividiert werden!')
   else  showmessage(intToStr(x) + '/' + intToStr(y) + ' = ' +
       floatToStr(x/y));
end;

4. Lektion: Schleife: "for .. to .. do .. " und "for .. to .. do Begin .. End"

Dazu:
Summen
Produkte
>
Motivation: Warum Summen und Produkte in der Mathematik so wichtig sind, sei an folgendem Beispiel erläutert 


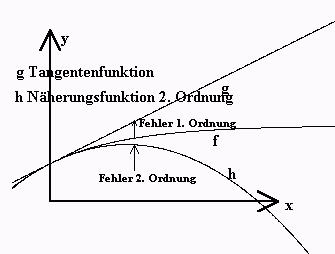
Für jede Funktion f ist die Tangentenfunktion g mit

g(x) = f(0) + f'(0)·x eine Näherung des Schaubildes in Q(0|f(0)).

(Der "Fehler 1. Ordnung" ist "nahe bei x=0" klein.)

Noch besser wird f durch eine Parabel angenähert, wenn man noch

die Krümmung durch die 2. Ableitung berücksichtigt:

                        1         2
h(x) = f(0) + f'(0)·x + -·f''(0)·x  (Siehe Schaubild!)
                        2

(Der "Fehler 2. Ordnung" ist "nahe x=0" kleiner).


Allgemein bestimmt man die ganzrationale Funktion g
                                                   n
                         2         n
mit g (x) = a + a x + a x + ... a x  als Näherungsfunktion so, dass
     n       0   1     2         n
                                                  (n)       (n)
g(0) = f(0), g'(0) = f'(0) , g''(0) = f''(0) ... g   (0) = f   (0).


Man erhält dann die "Taylorreihe" als Näherungsfunktion

                                                       (n)
               f'(0)     f''(0) 2   f'''(0) 3         f   (0)  n
g (x) = f(0) + —————·x + —————·x  + ——————·x  + ... + ———————·x
 n              1!         2!          3!                n!

Zum Beispiel für f(x) = sin(x) die "Taylorreihe"

    1   3  1   5  1   7
x - ——·x + ——·x - ——·x + ... mit n! = 1·2·3· ... ·n
    3!     5!     7!
Wie man π mit einer Summe oder Reihe berechnet: siehe Leibniz/Wallis/Euler etc. 		nf.gif
Fazit: Summen und Produkte sind in der numerischen Mathematik das "tägliche Brot". 

Um den Befehl showmessage('Hallo Welt'); 4 mal ausführen zu
lassen, kann man folgende Schleife verwenden:

procedure TForm1.Button1Click(Sender: TObject);
 var i:integer;
begin
 for i := 1 to 4 do showmessage(IntToStr(i) + ' Hallo Welt');
end;

Die folgende Prozedur ohne for .. to do macht genau dasselbe.

procedure TForm1.Button1Click(Sender: TObject);
 var i:integer;
begin
 i := 1; showmessage(IntToStr(i) + ' Hallo Welt');
 i := 2; showmessage(IntToStr(i) + ' Hallo Welt');
 i := 3; showmessage(IntToStr(i) + ' Hallo Welt');
 i := 4; showmessage(IntToStr(i) + ' Hallo Welt');
end;

Will man in einer Schleife mehrere Befehle ausführen lassen,
schreibt man diese zwischen Begin und End.

procedure TForm1.Button1Click(Sender: TObject);
 var i:integer;
begin
 for i := 1 to 10 do Begin
  showmessage(IntToStr(i) + ' Hallo Welt');
  showmessage('Dieses war der ' + IntToStr(i) + '. Streich');
  showmessage('Doch der nächste folgt zugleich');
 End;
 showmessage('Jetzt ist Schluss');
end;

Hinweis: In Delphi darf man groß- und kleinschreiben, wie man will.
     Hier wird deshalb zur besseren Lesbarkeit das erste,
     das zweite u.s.w. ineinandergeschachtelte begin mit
     zugehörigem end folgendermaßen geschrieben.
Merke! Auf jeden Fall mit Einrückungen schreiben.
begin ...
 Begin ...
  BEgin ...
   BEGin ...
     beGin ...
     ...
     enD;
   END;
  ENd;
 End;
end;

Anektdote (Typisch deutsch):

Die Polizei,
 die die Bankräuber,
  die die Sparkasse in Weiler,
   die neben dem Rathaus,
    das vom berühmten Architekten,
     der auch das Rathaus in Oberdorf,
      das kürzlich
      abbrannte,
     gebaut wurde,
   steht,
  überfielen,
 verfolgte,
hatte Erfolg.
Wer jetzt noch keine Graphik kennenlernen will, kann den folgenden Einschub überspringen und gleich zu Summen springen.

Programm: Zeichne Parabel y = v*x2

Zum folgenden Programm benötigen wir folgende Begriffe: 
 Screen.Width ist die Breite des Bildschirms
 Screen.Height ist die Höhe des Bildschirms
Unsese Form hat verschiedene Eigenschaften:
Zum Beispiel:
  form1.Width  (Breite)
  form1.Height (Höhe)
  form1.Top   (Obere Rand im Vergleich zum Bildschirm)
  form1.left  (Linker Rand im Vergleich zum Bildschirm)
Komplizierter ist die Eigenschaft 
  form1.canvas
  canvas (engl.) = Leinwand
Das ist die Zeichenfläche von Form1.
Darauf kann gezeichnet werden:

——————————————>
1. Koordinate nach rechts
|
|
| x
| (200|100) in Pixel
|
|
2. Koordinate nach unten

form1.Canvas.Rectangle(100,100,200,200)
zeichnet ein Rechteck: links oben (100|100) rechts unten (200|200) 
form1.Canvas.Ellipse(100,100,200,200)
zeichnet eine Ellipse, die das Rechteck oben an allen Seiten berührt 
mit form1.Canvas.Pen.Width := 5;
   form1.Canvas.Pen.Color := clblue; //cl = Color
wird die Dicke und Farbe unseres Schreibstiftes bestimmt.
Das Rechteck wird folgendermaßen mit der Pinselfarbe rot eingefärbt:
form1.Canvas.brush.Color := clRed;
Eine Linie von A(100|100) nach B(200|200) wird folgendermaßen gezeichnet: form1.canvas.moveto(100,100); form1.Canvas.LineTo(200,200);

Programm 


//Button1 und button2 auf ein panel mit panel1.align := bottom;
procedure TForm1.Button1Click(Sender: TObject); //Vorbereitung
begin
 top := 0;
 left := 0;
 //form1.width := screen.Width; Kürzer nur ...
 width := screen.Width;  //width bezieht sich hier auf den Typ TForm1
 height := screen.height;
 //panel1.Align := albottom; im Objektinspector
 canvas.Pen.Width := 0;
 canvas.Brush.Color := clwhite;
 canvas.Rectangle(0,0,width,height);
end;

procedure TForm1.Button2Click(Sender: TObject);
  var x, yi: integer; //yi = y_integer
    yr, v: real;  //yr = y_real
begin
 canvas.Pen.Width := 5;
 canvas.Pen.Color := clred;
 canvas.Brush.Color := clyellow;
 v := height/(width*width);
 for x := 0 to width do Begin
  yr := v*x*x;
  yi := round(yr);
  canvas.Ellipse(x,yi,x + 10,yi + 10); //nur Integer erlaubt
 End;
end;

I) Summen können mit folgenden zwei Zeilen gebildet werden:
  s := 0; //Anfangswert: das neutrale Element bez. " + "
  for i := .. to .. do s := s + ..

Beispiel 4.1 s = 1 + 4 + 9 + 16 + .. + 10*10


procedure TForm1.Button1Click(Sender: TObject);
 var s,i:integer;
begin
 s := 0; //Anfangswert
 for i := 1 to 10 do
  s := s + i*i; //Hier wird "aufaddiert"
 showmessage('s=' + intToStr(s)); //385
end;

Hinweis: Ein schwerer Programmierfehler wäre es, den Anfangswert
     s := 0 nicht zu setzten. Für s ist zwar eine
     Speicherstelle reserviert. Diese ist jedoch noch nicht
     initialisiert. Der Compiler gibt deshalb eine Warnung aus.
     Diese Warnungen zu beachten, hat sich bestens bewährt.

Die for .. to .. do-Schleife ersetzt die in der folgenden Prozedur
beschriebenen 20 Befehle:

procedure TForm1.Button1Click(Sender: TObject);
 var s,i:integer;
begin
 s := 0;
 i := 1; s := s + i*i; //1
 i := 2; s := s + i*i; //1 + 4
 i := 3; s := s + i*i; //5 + 9
 i := 4; s := s + i*i; //14 + 16
 i := 5; s := s + i*i; //30 + 25
 i := 6; s := s + i*i; //55 + 36
 i := 7; s := s + i*i; //91 + 49
 i := 8; s := s + i*i; //140 + 64
 i := 9; s := s + i*i; //204 + 81
 i := 10; s := s + i*i;//285 + 100
 showmessage('s=' + intToStr(s)); //385
end;



II) Produkte können mit folgenden zwei Zeilen gebildet werden:
  p := 1; //Anfangswert: das neutrale Element bez. "*"
  for i := .. to .. do p := p * ..

Beispiel 4.2 p := 6! = 1*2*3* .. *6

procedure TForm1.Button1Click(Sender: TObject);
 var p,i:integer;
begin
 p := 1;
 for i := 1 to 6 do p := p*i;
 showmessage('p=' + intToStr(p));
end;

Ohne Schleife müsste man folgendes schreiben.
(Als Kommentar ist die Wertebelegung protokolliert.
 Das ist stets eine gute Übung beim Programm studieren).

procedure TForm1.Button1Click(Sender: TObject);
 var p,i:integer;
begin
 p := 1;
 i := 1; p := p*i; //p=1
 i := 2; p := p*i; //p=1*2
 i := 3; p := p*i; //p=2*3
 i := 4; p := p*i; //p=6*4
 i := 5; p := p*i; //p=24*5
 i := 6; p := p*i; //p=120*6
 showmessage('p=' + intToStr(p)); //p=720
end;

Aufgabe 4.1: Schreibe ein Programm, das berechnet:

 a) s = 1 + 1/2 + 1/3 + 1/4 + ... + 1/9999

 b) s = 1000 + 1001 + .. + 1998 + 1999

 c) p = 2^32 = 2*2*2* .. *2

Lösung


Verallgemeinerung: Nach Eingabe eines Wertes in ein Editfeld soll
          eine Summe bzw. ein Produkt berechnet werden.
(OOP: Die Editkomponente kannst du von der Komponententabelle als
   edit1 auf die Form platzieren)

   Lösung mit n als integer:
   n := stringToInt(edit1.text);
   for i := 1 to n do ..

Beispiel 4.3 xn: x hoch n
     Man benötigt edit1 für n und edit2 für x.

procedure TForm1.Button1Click(Sender: TObject);
 var i,n:integer;
   p,x:real;
begin
 n := strToInt(edit1.text);
 x := strToFloat(edit2.text);
 p := 1;
 for i := 1 to n do p := p*x;
 showmessage(floatToStr(x) + '^' + intToStr(n) + '=' + floatToStr(p));
end;

Aufgabe 4.2: Was berechnet folgendes Programm bei Eingabe von
       a) n=5    (Keine Zahl sondern Rechenausdruck!)
       b) n=10
       c) allgemein
procedure TForm1.Button1Click(Sender: TObject);
  var i,n,plusminus:integer;
    s,p:real;
begin
 n := strtoInt(edit1.text);
 plusminus := 1;
 s := 1;
 for i := 1 to n do Begin
  plusminus := - plusminus;
  s := s + plusminus/(2*i + 1);
 End;
 showmessage(floatToStr(s));
 p := 4*s;
 showmessage(floatToStr(p));
end;

Lösung

5. Lektion: For-, repeat und while-Schleifen

for .. to .. do ..
for .. to .. do Begin .. End
repeat .. until ..
while .. do ..
while .. do Begin .. End
Dazu
Wertetafeln
die Komponente memo1
Die Eigenschaft memo1.lines
Die Methoden memo1.lines.add(..) und memo1.lines.clear 


Beispiel 5.1: Wertetafel für y = 1/3x^3 - 3x von -5 bis 5
Man benotigt außer dem Button noch eine Memokomponente.

procedure TForm1.Button1Click(Sender: TObject);
 var x :integer;
   y :real;
begin
 memo1.Lines.clear;
 for x := -5 to 5 do Begin
  y := 1/3*x*x*x - 3*x;
  memo1.lines.Add(IntToStr(x) + '  ' + FloatToStr(y));
 End;
end;

Bemerkung:
Hier verwenden wir eine äußerst nützliche Komponente, nämlich die Komponente memo.

Komponenten kann man als Programmteile betrachten, die "gekapselt" programmiert sind. Der Benutzer braucht nicht den Quellcode verstehen. Er muss nur die Eigenschaften wie zum Beispiel memo1.lines.count und Methoden wie zum Beispiel memo1.lines.add(..) kennen. Er muss also das Rad nicht neu erfinden.

Verwende andererseits nicht für jede Kleinigkeit, die man auch selbst mit Hilfe der Standardkomponenten programmieren kann, eine spezielle Komponente. Die Suche nach einer Komponente wie zum Beispiel "Wertetafel" wäre vielleicht erfolgreich. Aber bis du ihre Funktionen erfasst hast, wirst du ein passendes Programm selbst programmiert haben. Und: Ein selbst geschriebenes Programm funktioniert genau so, wie du es dir vorstellst. 
Aufgabe 5.1: Schreibe ein Programm das die Wertetafel
       für eine Funktion ausgibt.
       Die Grenzen soll der Benutzer eingeben können.

Lösung

Aufgabe 5.2: Was berechnet folgendes Programm

procedure TForm1.Button1Click(Sender: TObject);
 var x :integer;
   y :real;
begin
 memo1.Lines.clear;
 for x := -36 to 36 do Begin
  y := sin(10*x*Pi/180); //sin berechnet den Sinus im Bogenmaß
  //Beachte: x im Bogenmaß ist x*Pi/180 im Gradmaß
  memo1.lines.Add(IntToStr(x) + '0  ' + FloatToStr(y));
 End;
end;

Lösung

Beispiel 5.2: Wertetafel von x1 bis x2 mit Schrittweite s mit
repeat .. until ..:

procedure TForm1.Button1Click(Sender: TObject);
 var x, x1, x2, s, y:real;
begin
 x1 := -2;  //Alternative: Einlesen von editx1
 x2 := 2;  //Alternative: Einlesen von editx2
 s :=  1/10; //Alternative: Einlesen von edits
 x := x1; //Anfangswert
 repeat
  y := 1/3*x*x*x - 3*x;
  memo1.lines.Add(FloatToStr(x) + '  ' + FloatToStr(y));
  x := x + s;
 until x > x2; //Programmierfehler wäre .. until x = x2 bzw.
        //until x = x2 + s, da real nur angenähert rechnet!
        //siehe auch Gleitkommarechnung
end;
Hier wird x laufend um s = 0.1 erhöht, bis es schließlich x2 = 2 übertrifft. Solange der Ausdruck nach until nicht den Wert true hat, wird der Teil zwischen repeat und until wiederholt. Erst wenn, x = 2.1 ist also 〈x2 den Wert false hat, gibt es keine Wiederholung mehr.
Beispiel 5.3: Wertetafel von x1 bis x2 mit Schrittweite s mit
while .. do Begin .. End;

procedure TForm1.Button1Click(Sender: TObject);
 var x, x1, x2, s, y:real;
begin
 x1 := -2;  //Alternative: Einlesen von editx1
 x2 := 2;  //Alternative: Einlesen von editx2
 s :=  1/10; //Alternative: Einlesen von editx2
 x := x1;  //Anfangswert
 memo1.Lines.clear;
 while x 〈= x2 do Begin
  y := 1/3*x*x*x - 3*x;
  memo1.lines.Add(FloatToStr(x) + '  ' + FloatToStr(y));
  x := x + s;
 End;
end;
Solange die Bedingung x 〈 x2 nach while den Wert true hat, wird der Befehl nach while ... wiederholt. Da nach while eine Befehlsguppe von drei Befehlen steht, muss diese Gruppe zwischen Begin und End.

Beispiel 5.4 Aus einer endlichen oder unendlichen Schleife kann man mit exit herausspringen.

Im Beispiel mußt Du ein Shape auf dem Formular plazieren. ("Shape" findest Du bei Delphi 5 auf der Komponentleiste "Zusätzlich"). Gestalte es nach Deinen Wünschen, zum Beispiel als eine kleine Ellipse. Du braucht dazu zwei globale Variablen "stop" und "geschwindigkeit". Diese werden vor "implementation" nach "Form1: TForm1" deklariert.

Beim "Startbutton" setzt sich shape1 in Bewegung bis zum rechten Rand, dann springt es wieder nach links und bewegt endlos sich wieder nach rechts.

repeat
 das shape bewegt sich ohne Unterlass
until false; //Die Bedingung nach until wird nie wahr.
Mit einem zweiten Button kann jedoch die Bewegung gestoppt werden. Die Variable "stop" wird auf true gesetzt. Sobald dies der Fall ist wird die Endlosschleife "repeat ... until false" mit exit verlassen. Dass die Botschaft auch ankommt, wird durch "application.ProcessMessages" bewirkt. (Das veranlasst Windows alle Botschaften, die es erhalten hat, erst einmal abzuarbeiten. Zum Beispiel auch, das Shape weiter rechts zu zeichnen.).

Mit einem 3. Button schließlich wird die geschwindigkeit erhöht.

Zu erwähnen bleibt noch, dass "DoubleBuffered := true" das Flackern verhindert.
Hier das ganze Programm. 
var
 Form1: TForm1; //... schreibt Delphi. Darunter schreibst Du die
         // globalen Variablen "stop" und "geschwindigkeit"
 stop: boolean;
 geschwindigkeit: integer;

implementation //... schreibt Delphi

{$R *.DFM} // ... schreibt Delphi

procedure TForm1.Button1Click(Sender: TObject);
begin
 DoubleBuffered := true;
 stop := false;
 geschwindigkeit := 1;
  repeat
  if stop then exit;
  shape1.Left := shape1.Left + geschwindigkeit;
  if shape1.Left 〉 form1.Width - shape1.Width - 20 then 
    shape1.Left := 0;
  application.ProcessMessages;
 until false;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
 stop := true;
end;

procedure TForm1.Button3Click(Sender: TObject);
begin
 geschwindigkeit := geschwindigkeit + 1;
end;



Aufgabe 5.3: Schreibe die Prozeduren so um, dass
Anfangs- und Endwert sowie die Schrittweite eingelesen werden
können.
Lösung

Überprüfe dein Können! 


Aufgabe 5.4: Was berechnet folgendes Programm ?
       Denke Dir nach jedem Befehl "showmessage(...)"
       und schreibe ein Verlaufsprotokoll.

a)  procedure TForm1.Button1Click(Sender: TObject);
    var a,b,c,d,x,y: integer;
   begin
    a := 2; b := -10; c := 0;
    a := a + 4; b := b + 4 ; c := c + 4;
    a := b + c; b := a + c; c := a + b;
    x := 7;
    x := x*x;
    x := x*x; //Darstellung als Potenz mit kleinster Basis erwünscht!
    y := x;
    x := x*x;
    x := x*x;
    y := x*y;
   end;

b) procedure TForm1.Button1Click(Sender: TObject);
    var a,b,c,d,w,x:real;
   begin
    a := 6; b := -5; c := -25;
    d := b*b - 4*a*c;
    w := sqrt(d); //sqrt=Quadratwurzel
    x := (-b - w )/(2*a);
   end;

c) procedure TForm1.Button1Click(Sender: TObject);
    var k,a: integer;
      x: real;
   begin
    x := 0;
    for k := 1 to 6 do Begin
     a := k*k;
     x := x + 1/a; //Rechenausdruck genügt
    End;
   end;

d) procedure TForm1.Button1Click(Sender: TObject);
    var k,a: integer;
      x: real;
   begin
    x := 0;
    k := 1;
    repeat
     a := k*k;
     x := x + 1/a; //Rechenausdruck genügt
     k := k + 2;
    until k > 6;
   end;

e)  procedure TForm1.Button1Click(Sender: TObject);
    var k,a,b: integer;
      x: real;
   begin
    x := 1;
    k := 1;
    while k 〈 6 do Begin
     a := 2*k;
     b := 2*k + 1;
     x := x * a/b; //Rechenausdruck genügt
     k := k + 1;
    End;
   end;

Lösung

Aufgabe 5.5: Schreibe jeweils ein Programm!

 a) Die Wertetafel für y = x^2 - 2x soll für
   die Werte x = -2; -1,9; ... 1,6; 1,7 1,8; 1,9 und 2
   in ein Memofeld geschrieben werden.

   (i)  Mit einer for  -Schleife.
   (ii) Mit einer while -Schleife.
   (iii) Mit einer repeat-Schleife.

 b) In ein Editfeld soll die natürliche Zahl n eingegeben werden
   können. Anschließend soll die Summe
   s = 1 + 1/4 + 1/9 + 1/16 + ... + 1/(n*n)
   berechnet werden und in eine zweites Editfeld geschrieben
   werden.

 c) In zwei Editfeldern sollen die natürlichen Zahlen
   a und b eingegeben werden (a 〈 b)
   Anschließend soll das Produkt p = a*(a + 1)*(a + 2) ... *(b-1)*b
   berechnet werden.

Lösung

Aufgabe 5.6:

  Schreibe ein Programm, welches das kleinste n ausgibt,
  für das s = 1 + 1/2 + 1/3 + 1/4 + ... + 1/n > 20 ist.

Lösung
Aufgabe 5.7: Ein Selbständiger hat ein Vermögen von 1,674 Mio. EUR. Er rechnet mit einem Verbrauch von 48 000 EUR jährlich, jedes Jahr 5% mehr. Wir nehmen an, dass das Restvermögen auch zu 5 % verzinst wird. Wie lange kann er unter diesen Voraussetzungen von seinem Vermögen zehren?
Schreibe dazu ein Programm. 
Mathematische Lösung:
 Anfangsvermögen     K0 = 1674000
 Anfangsauszahlung    a0 = 48000;
 Vermögen nach 1 Jahr   K1 = (K0 - a0)*1.05
 Auszahlung nach 1 Jahr  a1 = a0*1.05
 Vermögen nach 2 Jahren  K2 = (K1 - a1)*1.05
    ...
 Auszahlung nach n Jahren an = an-1*1.05
 Vermögen nach n Jahren  KN = (Kn-1 - an-1)*1.05
Lösung


Weitere Aufgaben mit Lösungen