Die Homepage von Joachim Mohr
11. Lektion: Strukturiertes Programmieren: Prozeduren I. Teil
Beispiele geändert (vereinfacht): Januar 2004- Prozeduren dienen wie Funktionen dazu:
- Programme übersichtlicher zu machen.
- Wiederverwendbaren Quelltext zu schreiben.
ax2 + bx + c = 0
hat die Lösung
- b ± sqrt(b·b - 4ac)
x = —————————————————————
1,2 2a
Dabei hängt die Anzahl der Lösungen noch von der
Diskriminante d = b·b - 4ac ab: Keine Lösung für d < 0, eine Lösung für d = 0 und 2 Lösungen für d > 0.
Die folgende überall wiederverwendbare Prozedur hat als Eingangsparameter die Variablen a, b und c und als Ausgangsparameter die Variablen Anzahl, x1 und x2.
Merke: Ausgangsvariablen werden mit dem Schlüsselwort var in der Prozedur deklariert. Nur dann können Sie verändert werden.
Genau genommen: die Prozedur legt für Eingangsvariablen(Wertparameter) eine Kopie der Variablen im Speicher an. Werden die Eingangsvariablen in der Prozedur verändert, hat dies woanders keine Auswirkungen.
Ausgangsvariablen (Variablenparameter) verwendet jedoch die ursprüngliche Variable, d.h. die Speicherstelle der Variablen, mit der die Prozedur aufgerufen wird, wird überschrieben. Eine Änderung bleibt so nach Aufruf der Prozedur erhalten.
Der Funktionsaufruf könnte dann so aussehen: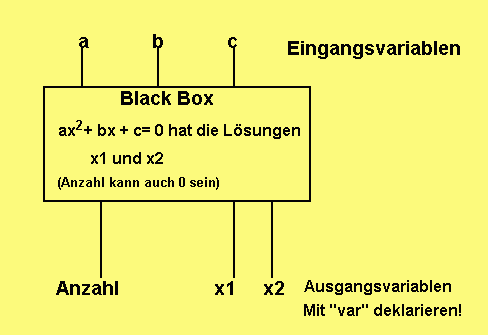
procedure QuadrGl(a,b,c: real; var anzahl: Integer; var x1,x2: real); var d: real; begin d := b*b - 4*a*c; if d < 0 then Anzahl := 0 else if d = 0 then Begin Anzahl := 1; x1 := -b/(2*a); End else Begin anzahl := 2; x1 := (-b + sqrt(d))/(2*a); x2 := (-b - sqrt(d))/(2*a) End; end;
procedure TForm1.Button1Click(Sender: TObject);
var anz: integer;
x1,x2: real;
begin
QuadrGl(1,5,6,anz,x1,x2);
if anz = 0 then showmessage('Keine Lösung') else
if anz = 1 then showmessage('Eine Lösung: x ='+floatToStr(x1))
else showmessage('Lösungen: x1=' + FloatToStr(x1) + ' x2=' + FloatToStr(x2));
end;
Natürlich können im Hauptprogramm die Variablen beliebige Namen bekommen.
Auch andere als in der Prozedur. Zum Beispiel:
procedure TForm1.Button1Click(Sender: TObject);
var z: integer;
u,v: real;
begin
QuadrGl(1,5,6,z,u,v);
if z = 0 then showmessage('Keine Lösung') else
if z = 1 then showmessage('Eine Lösung: x ='+floatToStr(u))
else showmessage('Lösungen: x1=' + FloatToStr(u) + ' x2=' + FloatToStr(v));
end;
Wird wie hier zum Beispiel quadrGl(1,5,6,z,u,v) aufgerufen, sind nachher die Variablen z, u und v
mit den Werten
z=2 u=-2 v=-3belegt. In der Prozedur sind a,b,c Werteparameter und z, x1 und x2 Variablenparameter.
Zusammenfassung:
Beim Aufruf der Prozedur werden bei den Werteparametern, im Beispiel a,b,c, Speicherplätze für die Werte von a, b und c reserviert und beim Verlassen der Prozedur wieder freigegeben.Anders ist es bei den Variablenparametern, im Beispiel Anzahl,x1 und x2. Die Prozedur bekommt mitgeteilt, wo im Hauptprogramm Speicherplatz für Anzahl,x1 und x2 reserviert ist (mittels "Zeiger"), von dort entnimmt sie die Werte, falls benötigt (im Beispiel nicht), und überschreibt (wie im Beispiel) die Werte, die dann im Hauptprogramm verwendet werden können.
Aufgabe 11.1: Schreibe das Programm so um, dass die Eingangsvariablen in drei Editfeldern eingeben werden können.
Lösung
Aufgabe 11.2 Schreibe ein Programm, das nach Eingabe von Radius und Höhe das Volumen und die Oberfläche eines Kegels ausgibt. Trenne zwischen Eingabe und Ausgabe procedure button1click ... und der Berechnungsprozedur procedure Kegel.... (Beim Kegel ist die Oberfläche O = Pi·r·(r+s), wobei s die Seitenkante ist. Die Formel für's Volumen V = 1/3Pi·r^2·h ist allgemein bekannt.)
Lösung
Aufgabe 11.3 Schreibe ein Programm, das nach Eingabe der Seitenlängen eines Dreiecks, die Winkel ausgibt. Kapselung die Berechnungen wieder in eine Prozedur. (Verwende den Kosinussatz a^2 = b^2 + c^2 - 2b*c*cos(alpha) und al = ArcCos(x), wenn Cos(al) = x ist).
Lösung
Aufgabe 11.4 Das LGS (lineare Gleichungssystem)
ax + cy = e
bx + dy = f
hat die Lösung
x = (ed - cf)/det
y = (af - be)/det
für det = ad - bc
Bei det = 0 hat das LGS keine eindeutige Lösung.
Schreibe eine Prozedur mit Eingangsparameter a, b, c, d, e und f (real)
und Ausgangsparameter lsg (boolean) und x und y (real), das das LGS
löst. Die Variable lsg soll dabei true sein, wenn eine eindeutige Lösung
existiert. Löse mit der Prozedur dann das LGS
5x - 7y = 9
-3x + 2y = 4
Lösung
Beispiel 11.2 Bei diesen Beispielen gibt es nur Eingangsvariablen. Statt dass Ausgangsvariablen berechnet werden, werden geometrische Objekte gezeichnet.
Dazu musst du vom Komponentenreiter "Zusätzlich" das Image1 auf dein Formular platzieren. Das Image1 besitzt eine Zeichenfläche - "Canvas" genannt. Auf die kannst Du folgendermaßen eine Strecke zeichnen.
procedure ZeichneStrecke(a1,a2, b1, b2: integer); begin form1.image1.Canvas.Pen.Width := 3; //Die Dicke des Zeichenstiftes ist 3 form1.Image1.Canvas.MoveTo(a1,a2); //Beginn der Zeichnung bei (a1,a2) form1.Image1.Canvas.LineTo(b1,b2); //Ende der Zeichnung bei (b1,b2) //(a1,a2) ist auf der Zeichenfläche "a1 Pixel nach rechts und a2 Pixel nach unten" end;Kürzer:
procedure ZeichneStrecke(a1,a2, b1, b2: integer);
begin
with form1.Image1.Canvas do Begin
Pen.Width := 3;
MoveTo(a1,a2);
LineTo(b1,b2);
End;
end;
Die folgende Prozedur zeichnet ein Quadrat
procedure zeichneQuadrat(a1,a2,a: integer); begin ZeichneStrecke(a1,a2,a1+a,a2); //Seite oben ZeichneStrecke(a1+a,a2,a1+a,a2+a); //Seite rechts ZeichneStrecke(a1+a,a2+a,a1,a2+a); //Seite unten ZeichneStrecke(a1,a2+a,a1,a2); //Seite links end;Um dem ganzen noch etwas Farbe zu verleihen (und damit du siehst, wie man "brush" verwendet) färben wir unser image1 noch gelb ein:
procedure faerbegelb;
begin
with form1.Image1 do Begin
canvas.brush.Color := clyellow;
canvas.rectangle(0,0,width,height);
End;
end;
Unzählige Quadrate kann man dann im Hauptprogramm
zum Beispiel folgendermaßen zeichnen.
procedure TForm1.Button1Click(Sender: TObject);
var x, y: integer;
begin
Faerbegelb;
x := 0;
repeat
y := 0;
repeat
zeichneQuadrat(x,y,10);
y := y + 20;
until y > form1.Image1.height;
x := x + 20;
until x > form1.image1.Width;
end;
Das Ganze sieht dann folgendermaßen aus:

Nebenbei bemerkt: Ein Logo kann man leicht mit folgender Prozudur bewerkstelligen:
procedure TForm2.Button2Click(Sender: TObject);
begin
with Image1.Canvas do Begin
brush.Color := $FFFF00;
rectangle(0,0,image1.width,image1.height);
font.Size := 18;
font.Name := 'Comic Sans MS';
TextOut(100,5,'Tempo Tabellen Text');
brush.Color := $00BFFFBF;
ellipse(20,40,410,220);
font.size := 10;
TextOut(185,50,'(c) J. Mohr');
TextOut(165,70,'mit Bildbearbeitung');
End;
End;

Anhang: Mit "echten" Koordinaten zeichnen
Um mit echten Koordinaten zu zeichnen muß man zuerst die Koordinaten eine Punktes P(x|y) im Koordinatensystem in Pixelkoordinaten umrechnen: Siehe dazu folgendes Programm, das die Koordinatenachsen und eine Strecke von 0(0|0) nach P(5|5) zeichnet:
procedure KoordinatenInPixelkoordinaten(x,y: real; var xp,yp: integer);
const xmax = 10; //Durch Verändern dieser Werte, kannst du ...
ymax = 10; //... jeden beliebigen Maßstab einzeichnen.
{ | ymax
|
|
| x,y
|
———————————————————————— xmax
|
|
|
|
| }
var hoehe, breite, //Die Canvasdimensionen
xp1, xp2, yp1, yp2: integer; //die Pixelkoordinaten
{Lineare Funktion:
x-Werte: xp(0) = breite/2; xp(xmax) = breite
breite breite
=> xp(x) = —————— x + ——————
2*xmax 2
y-Werte: yp(0) = hoehe/2; yp(ymax) = 0
hoehe hoehe
=> yp(y) = - ————— y + —————
2*ymax 2 }
begin
breite := form1.image1.width;
hoehe := form1.image1.Height;
xp := round(breite/(2*xmax)*x + breite/2);
yp := round(- hoehe/(2*ymax)*y + hoehe/2);
end;
procedure ZeichneStrecke(a1,a2, b1, b2: real);
var ap1, ap2, bp1, bp2: integer;
begin
KoordinatenInPixelkoordinaten(a1,a2,ap1,ap2);
KoordinatenInPixelkoordinaten(b1,b2,bp1,bp2);
form1.Image1.Canvas.MoveTo(ap1,ap2);
form1.Image1.Canvas.LineTo(bp1,bp2);
end;
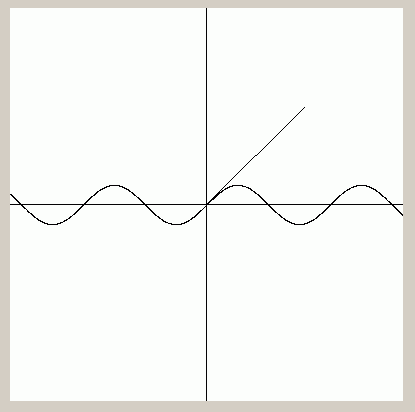
Im Hauptprogramm werden die Koordinatenachsen
gezeichnet sowie die Strecke von 0(0|0) bis P(5|5).
Und - weils so einfach ist - gleich noch die Sinuskurve, die aus lauter Streckenelementen zusammengesetzt wird.
procedure TForm1.Button1Click(Sender: TObject);
var x: real;
begin
form1.image1.Width := form1.image1.Height;
ZeichneStrecke(-10,0,10,0); //x-Achse
ZeichneStrecke(0,10,0,-10); //y-Achse
ZeichneStrecke(0,0,5,5); //Strecke von 0(0|0) nach P(5|5)
x := -10;
repeat
zeichneStrecke(x,sin(x),x+0.01,sin(x+0.01));
x := x + 0.01; //auf 1/100 LE genau
until x > 10;
end;
Um wieder viele Quadrate zu zeichen - ähnlich wie oben - kannst du dir das folgende Programm anschauen:
procedure zeichneQuadrat(a1,a2,a: real); //Nicht Neues (siehe oben)
begin
ZeichneStrecke(a1,a2,a1+a,a2); //jetzt unten
ZeichneStrecke(a1+a,a2,a1+a,a2+a); //rechts
ZeichneStrecke(a1+a,a2+a,a1,a2+a); //jetzt oben
ZeichneStrecke(a1,a2+a,a1,a2); //links
end;
procedure TForm1.Button1Click(Sender: TObject);
var x, y: integer;
begin
form1.image1.Width := form1.image1.Height;
for x := -8 to 8 do
for y := -8 to 8 do
ZeichneQuadrat(x,y,0.5);
end;
12. Lektion: Iterationsverfahren
Iteration bedeutet: "Schritt für Schritt".Hier betrachten wird Iterationsverfahren im engeren Sinne: Eine nicht perfekte Lösung wird Schritt für Schritt verbessert.
Aufgabe 12.1 Das klassische Beispiel für ein Iterationsverfahren ist das Heron-Verfahren zur Berechnung von sqrt(a) ("Quadratwurzel von a").
Anfangswert x0 = 1
Schritt für Schritt wird die Näherung für sqrt(a) verbessert:
1 a
x1 = -(x0 + ——)
2 x0
1 a
x2 = -(x1 + ——)
2 x1
1 a
x3 = -(x2 + ——)
2 x2
...
Kurz formuliert: x0 = 1
1 a
x = -(x + -) (n = 0, 1, 2, ...)
n+1 2 n xn
Schreibe ein Programm dazu! Wichtige Überlegung: Wann kann ich aufhören!
Lösung
Heron von Alexandrien, ca. 60 n.Chr., Verfasser eines Euklid-Kommentars. Viel bekannter ist er jedoch als "Programmierer" geworden. Zum Beispiel erfand er eine Konstruktion zum selbsttätigen Öffnen einer Tempeltür. Durch das Feuer auf dem Altar wird Luft erhitzt. Diese drückt Wasser aus einem Gefäß in ein anderes, das Seilrollen in Bewegung setzt. Durch Wachszargen in Walzen , die mit den Seilrollen verbundenen sind, läuft ein Programm ab, das die Seilrollen vorwärts und rückwärts bewegt ... Die Zuschauer erstarrten vor Andacht dieser göttlichen Kräfte.
Nachtrag: Begründung zum Heronverfahren:
Es sei x eine Näherung für sqrt(a),
etwa x < sqrt(a). Dann ist
1 1 a a
—— > ——————— und - > ——————— = sqrt(a)
x sqrt(a) x sqrt(a)
a
Wir sehen: ist x zu klein, dann ist - zu groß.
x
a
Umgekehrt gilt: ist x zu groß, dann ist - zu klein.
x
Und es gilt fast: Um was der eine Wert zu klein ist, ist der andere Wert zu groß.
Und damit ist klar: Mit dem Mittelwert von x und a/x erhalten wir eine bessere Näherung.
Wer das Newtonverfahren kennt: Die Iteration von Heron ist identisch mit dem Newtonverfahren zur Bestimmumg der Lösung von f(x) = a - x2.
Beispiel 12.1 Das Intervallhalbierungsverfahren zur Berechnung einer Nullstelle einer Funktion f.
Mathematischer Hintergrund: Eine stetige Funktion f hat im Intervall [a,b] mindestens eine Nullstelle, wenn
Hat man nun ein solches Intervall [a,b], so berechnet man den Mittelwert m = 1/2(a+b). Ist zufällig f(m) = 0 ist man fertig. Sonst betrachtet man das Vorzeichen von f(m).
Als verbessertes Intervall, in dem die Nullstelle liegt, nimmt man
[a, m], falls f(a) und f(m) verschiedenes Vorzeichen haben oder
[m, b], sonst.
Nach n Schritten ist die Nullstelle bis auf 1/2n·(b-a) genau.
Beispiel: f(x) = x3 - 7/3x - 20/27
Bei dieser Funktion findet man f(1) < 0 und f(2) > 0.
Mit folgendem Programm wird die Nullstelle auf 10-12 genau bestimmt:
Die gewählte Genauigkeit "eps=10-12" kann nicht beliebig verschärft werden. Sie hängt von der Implementierung der Genauigkeit des Typs "real" ab. Ist sie zu scharf gewählt, kann es passieren, dass die repeat-Schleife nie verlassen wird.
function f(x:real):real;
begin
result :=x*x*x - 7/3*x - 20/27
end;
function intervallh(a,b: real): real; //Vor (f(a)*f(b) < 0
const eps = 1E-12
var m: real;
begin //Die einfachste Form
repeat
m := (a+b)/2;
if f(m)*f(a) < 0 then b := m else a := m;
until abs(b-a) < eps;
//Die Profis setzen hier abs(b-a) < eps*(1+abs(a));
//Dann ist z.B. auch der Fall a=100000 berücksichtigt!
result := (a+b)/2;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x1, x2: real;
begin
x1 := strToFloat(edit1.text);
x2 := strToFloat(edit2.text);
if f(x1)*f(x2) < 0 then showmessage('Kein Vorzeichenwechsel')
else showmessage('Nullstelle=' + FloatToStr(intervallh(x1,x2)));
end;
Effizienter konnte man das Intervallhalbierungsverfahren folgendermaßen programmieren:
function intervallh(x1, x2: real):real; //Vor.: f(x1) und f(x2) verschiedenes Vorzeichen
var m, y1, ym:real;
n : integer;
begin
y1 := f(x1);
n := 0;
repeat
m := (x1 + x2)/2;
ym := f(m);
if abs(ym) < 1E-12 //Genauigkeit von real
then Begin
result := m;
exit;
End;
if ((y1 > 0) and (ym > 0)) or ((y1 < 0) and (ym < 0)) then Begin
x1 := m;
y1 := ym;
End else x2 := m;
n :=n + 1;
if n > 100 then Begin
showmessage('Nullstelle nicht gefunden');
exit;
End;
until abs(x2 - x1) < 1E-12;
result := (x1 + x2)/2;
end;
Die "Einfädelung", um alle Nullstellen zwischen - 10 und 10 zu finden,
könnte man folgendermaßen bewerkstelligen:
procedure TForm1.Button1Click(Sender: TObject);
var x: real;
begin
x := -10;
while x < 10 do Begin
if f(x) *f(x+0.1) < 0 then
memo1.lines.Add(floatToStr(intervallh(x,x+0.1)));
x := x + 0.1;
End;
end;
Bemerkung für Mathematiker: Beim "Sekantenverfahren" wird m := 1/2(a+b)
ersetzt durch die Abszisse
b - a
m := a - ——————————— · f(a)
f(b) - f(a)
des Schnittpunktes der Sekante durch P(a|f(a)) und Q(b|f(b)) mit der x-Achse.
Beim Newtonverfahren wird die Iteration nach dem "Einfädeln" (Genauigkeit 1/10) beschleunigt durch die Iteration: (x0 erste Näherung)
f(x0) f(x0+h) - f(x0-h)
x1 = x0 - —————— mit f'(x0) = ————————————————— für "kleines" h > 0.
f'(x0) 2·h
Das Programm dazu: Beispiel 12.2 Newtonverfahren mit "Einfädeln":
function f(x:real):real;
begin
result :=x*x*x - 7/3*x - 20/27
end;
function fs(x:real):real; //fs = f'
const h = 1E-12;
begin
result := (f(x + h) - f(x - h))/(2*h) //Ableitung numerisch
end;
function newton(x: real): real;
const eps=1E-12;
begin
repeat
x := x - f(x)/fs(x);
until abs(f(x)) < eps;
result := x;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x: real;
begin
x := -10;
while x < 10 do Begin
if f(x) *f(x+0.1) <= 0 then
memo1.lines.Add('NS ='+floatToStr(newton(x)));
x := x + 0.1;
End;
end;
Effizienter (f(x) wird weniger oft berechnet) und mit einer Sicherheitsabfrage,
falls das Newtonverfahren nicht
funktioniert (und solche Beispiel sind zu jedem Programm konstruierbar):
function newton(var x0:real): real;
var y0:real;
n:integer; //Bremse
begin
n := 0;
y0 := f(x0);
repeat
x0 := x0 - y0/fs(x0); //fs = f'
y0 := f(x0);
//form1.memo1.lines.add(FloatToStr(x0) + ' ' + FloatToStr(y0));
inc(n);
until (abs(y0) < 1E-15) or (n > 25);
if n > 25 then showmessage('Newtonverfahren funktioniert nicht!');
result := x0;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x, y1,y2: real;
begin
x := -10;
y1 := f(x);
while x < 10 do Begin
y2 := f(x + 0.1);
if y1*y2 <= 0 then
memo1.lines.Add('NS ='+floatToStr(newton(x)));
x := x + 0.1;
y1 := y2;
End;
end;
Überprüfe dein Können!
Aufgabe 12.2: Betrachte folgende Funktion f ! (sie verwendet fak(k)=k! und hoch(x,n)=xn )
function f(x: real; n:integer):real;
var k: integer;
begin
result := 0;
for k := 0 to n do result := result + 1/fak(k)*hoch(x,k);
end;
a) Was ist f(2,5) (Achtung: Parameter 2 und 5)? Rechenausdruck genügt!
(Hinweis b) Was passiert, wenn man f(2,-5) berechnen will?
Aufgabe 12.3: Gegeben ist folgende Funktion.
function f(n: integer):real;
begin
if n = 0 then result := -1 else result := -n/2*f(n-1);
end;
a) Was ist f(5)? (Rechenausdruck genügt!) b) Was passiert, wenn man f(-5) berechnen will?
Aufgabe 12.4: Gegeben ist folgende Funktion.
function f(n: integer):real;
begin
if n <= 1 then result := 1 else result := n/2*f(n-1) + n/3*f(n-2);
end;
a) Was ist f(4)? (Rechenausdruck genügt!)
b) Was passiert, wenn man f(-5) berechnen will?
Aufgabe 12.5: Auch Prozeduren dürfen rekursiv sein (sich selbst
aufrufen). Was wird bei folgendem Programm ins Memo geschrieben?
procedure p(n: integer);
var k: integer;
s: string;
begin
if n > 0 then Begin
s:= '';
for k := 1 to n do s := s + '*';
form1.memo1.lines.add(s);
p(n-2);
End;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
p(10);
end;
Aufgabe 12.6: Schreibe eine Funktion
"function newton(x0: real): real", die nach Eingabe des Startwertes
x0 eine Nullstelle der Funktion f nach dem Newtonverfahren
xn+1= xn - f(xn)/fs(xn) berechnet.
Es wird vorausgesetzt, dass die Funktion f und deren Ableitung fs schon im Programm definiert sind.
Das Verfahren soll abbrechen, wenn ein Wert x mit |f(x)| < 1E-9 ermittelt ist. (Dies wird nach endlich vielen Schritten vorausgesetzt.)
Zusatz: Baue eine weitere Abbruchbedingung ein, falls nach 25 Schritten noch kein Ergebnis in Sicht ist.
Aufgabe 12.7: Das folgende Programm berechnet nach dem Intervall- halbierungsverfahren eine Nullstelle der Funktion f.
function f(x: real):real; //Könnte auch viel komplizierter sein!
begin
result := x*x - 2;
end;
function intervallh(x1, x2: real):real;
var m:real;
begin
repeat
m := (x1 + x2)/2;
if f(x1)*f(m) < 0 then x2 := m else x1 := m;
until abs(x2 - x1) < 1E-15;
result := (x1 + x2)/2;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x1, x2:real;
begin
x1 := strTofloat(edit1.text);
x2 := strTofloat(edit2.text);
showmessage(floatToStr(intervallh(x1,x2)));
end;
Ändere das Programm in folgenden Punkten:
(a) falls f(x1) und f(x2) gleiches Vorzeichen haben, soll
die Funktion "intervallh" nicht aufgerufen werden.
(b) Die Abbruchbedingung von "intervallh" soll
|(f(m)| < 1E-15 sein.
(c) Schreibe statt repeat die Funktion mit while.
Zusatz:
(d) Stell Dir vor, die Berechnung von f(m) dauere sehr lange.
Deshalb soll doppelte Berechnung vermieden werden.
Speichere deshalb f(x1) und f(m) in den Variablen
y1 bzw. ym und verwende y1 bzw. ym, falls f(x1) bzw.
f(m) zum zweiten Mal gebraucht werden.
Aufgabe 12.8 Schreibe eine Funktion "dritteWurzel(a)", die
die 3. Wurzel von a (0 ≤ a) als Lösung der Funktion Aufgabe 12.9 Schreibe eine Funktion "vierteWurzel(a)", die die 4. Wurzel von a (0 ≤ a) als Lösung der Funktion
Lösung
13. Lektion: Rekursion 2. Teil
"Iterativ arbeiten ist menschlich, rekursiv arbeiten ist göttlich"Anonym
Rekursionen sind erstaunlich kurze, leicht verständliche und effiziente Algorithmen.
In der Lektion "Sortieren" werden wir davon ausgiebig Gebrauch machen.
Hier noch ein paar einfachere Algorithmen.
Beispiel 13.1: pos(nadel,heuhaufen) ermittelt die Position des ersten Vorkommens vom String Nadel im String Heuhaufen. Die folgende Prozedur pos_n liefert die Position des i-ten Vorkommens.
function copyab(const s:string; const i:integer):string; //Rest von s ab i. em Zeichen
begin result:=copy(s,i,length(s)-i+1) end;
function pos_n(const a: string; b: string; n: integer): integer;
var k:integer;
begin
if n <= 1 then result := pos(a,b) else Begin
k := pos(a,b);
if k = 0 then result := 0 else BEgin
b := copyab(b,k+1);
result := pos_n(a,b,n-1); //rekursiv
if result >0 then result:=k+result;
ENd;
End;
end;
Aufgabe 13.1 Schreibe ein rekursive Funktion,
die als Ergebnis das n-te Wortin einem Text ermittelt.
Die einzelnen Wörter sind durch eine Leerzeichen voneinander getrennt.
Zum Beispiel ist in 'aaa bbb ccc ddd' das dritte Wort 'ccc'. Lösung
Beispiel 13.2: Rekursion ist bestens geeignet für einen Formelauswerter.

Ein schönes Beispiel, wie man Graphik rekursiv programmieren kann ist die Kochkurve.
Quelltext siehe Downloadseite "Schneeflockepas.zip"
Folgende Funktionen werden dort verwendet:
procedure pv(r,th: real); //polarvektor
var rad: real;
begin
rad := th*pi/180;
with form1.Image1.Canvas do
lineTo(round(penpos.x + r*cos(rad)),
round(penpos.y + r*sin(rad)));
end;
procedure fraktaleLinie(ordnung: integer; l, th:real);
begin
if ordnung = 0 then pv(l,th) else Begin
fraktaleLinie(ordnung - 1, l/3,th);
fraktaleLinie(ordnung - 1, l/3,th - 60);
fraktaleLinie(ordnung - 1, l/3,th + 60);
fraktaleLinie(ordnung - 1, l/3,th);
application.ProcessMessages;
End;
end;
Im Hauptprogramm steht nur noch:
form1.Image1.Canvas.moveTo(100, 150); fraktaleLinie(ordnung,L,0); fraktaleLinie(ordnung,L,120); fraktaleLinie(ordnung,L,240);
Den Rest des Kapitels kannst Du ruhig überspringen. Er ist nur für Spezialisten gedacht:
- Intervallhalbierungs- und Newtonverfahren rekursiv: Beispiel 13.3 und 13.4. Vergiss es!
- Alle Daten einer Festplatte auflisten: Beispiel 13.5. Siehe auch die FAQ
- Ein mathematischer Parser (Formelinterpreter). Lohnt sich, zu studieren!
- Lektion 14: Ordnungsalgorithmen. Pflicht für alle Informatiker!
- Backtracking am Beispiel eines Irrgartens. Verblüffend einfach!
- Der (erweiterte) Euklidische Algorithmus
Beispiel 13.3 und 13.4 sind nicht nur für Spezialisten!
Die Bestimmung von Nullstellen nach dem Intervallhalbierungsverfahren kann man auch rekursiv formulieren.
Beispiel 13.3 Intervallhalbierungsverfahren rekursiv.
Hinweis: Dieses Beispiel kannst Du ruhig überspringen. Die Iteration ist dafür die geignetere Methode (Die Rekursion steht hier nur zum Vergleichen.)
function Intervallhalbierung(x1, x2: real):real;
const Genauigkeit = 1E-15;
var xm, y1, ym:real;
begin
xm := (x1+x2)/2;
//Intervall [a,b] klein genug?
if abs(x2 - x1) < Genauigkeit then Begin
result := xm;
exit;
End;
y1 := f(x1);
ym := f(xm);
//Test form1.memo1.lines.add(FloatToStr(xm) + ' ' + FloatToStr(ym));
//Prüfung, in welchem Intervall die Nullstelle ist. Rechts oder links?
if ((y1 >= 0) and (ym >= 0)) or ((y1 <= 0) and (ym <= 0)) then
result := Intervallhalbierung(xm, x2) else //halbes Intervall rechts
result := Intervallhalbierung(x1,xm); //halbes Intervall links
//rekursiv bestechend übersichtlich!
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, b, fa, fb: real;
begin
a := 1;
b := 2;
//Ab hier a, b und f beliebig
fa := f(a);
fb := f(b);
showmessage('f(' + FloatToStr(a) +')=' + FloatToStr(fa)+#13+
'f(' + FloatToStr(b) +')=' + FloatToStr(fb));
if fa*fb >= 0 then showmessage('Abbruch: f(a)*f(b) > =0') else
showmessage('Nullstelle x =' + floatToStr(Intervallhalbierung(a,b)));
end;
Bemerkung: Im Gegensatz zum Iterationsverfahren, werden hier bei
jedem Schritt zwei y-Werte y1 und ym berechnet. Gleich viele Rechnungen
wie im Iterationsverfahren benötigt folgende rekursive Funktion:
function Intervallhalbierung(x1, x2: real; var y1:real):real;
const Genauigkeit = 1E-15;
var xm, ym:real;
begin
xm := (x1+x2)/2;
if abs(x2 - x1) < Genauigkeit then Begin
result := xm;
exit;
End;
//y1 := f(x1) entfällt hier
ym := f(xm);
//Test form1.memo1.lines.add(FloatToStr(xm) + ' ' + FloatToStr(ym));
//Prüfung, in welchem Intervall Nullstelle ist. Rechts oder links?
if ((y1 >= 0) and (ym >= 0)) or ((y1 <= 0) and (ym <= 0)) then
result := Intervallhalbierung(xm, x2, ym) else
result := Intervallhalbierung(x1,xm, y1);
end;
Beispiel 13.4 Nullstellenbestimmung mit "Einfädeln" nach dem
Intervallhalbierungsverfahren und beschleunigte Berechnung nach dem Newtonverfahren.
Im "Hauptprogramm" Button1Click wird in einem großen Intervall "abgetastet", ob die Funktion einen Vorzeichenwechsel hat. Ist dies der Fall, wird die "eingefangene" Nullstelle berechnet.
function f(x:real):real;
begin
result :=x*x*x - 7/3*x - 20/27
end;
function fs(x:real):real; //fs = f'
const h = 1E-12; //Ableitung Näherungsweise
begin
result := (f(x + h) - f(x - h))/(2*h)
end;
function Intervallhalbierung(x1, x2: real):real;
const Genauigkeit = 1/100; //fürs "Einfädeln"
var xm, y1, ym:real;
begin
xm := (x1+x2)/2;
if abs(x2 - x1) < Genauigkeit then Begin
result := xm;
exit;
End;
y1 := f(x1);
ym := f(xm);
if ((y1 >= 0) and (ym >= 0)) or ((y1 <= 0) and (ym <= 0)) then
result := Intervallhalbierung(xm, x2) else
result := Intervallhalbierung(x1,xm);
end;
function newton(x:real; n:integer):real;
const Genauigkeit =1E-12; //nicht zu klein, da fs nur numerisch
var y, ys:real;
begin
y := f(x);
if abs(y) < Genauigkeit then Begin
result := x;
exit;
End;
ys := fs(x);
//test form1.memo1.lines.add(FloatToStr(x) +
//' ' + FloatToStr(y) + ' ' + FloatToStr(ys));
dec(n); //n zählt ... 3, 2, 1, 0. Dann ist Schluss.
if (abs(ys) < Genauigkeit) or (n < 0) then Begin
showmessage('Newtonverfahren fehlgeschlagen');
result := 0;
exit;
End;
result := newton(x - y/ys,n - 1);//rekursiv
end;
function NullstelleZwischen(a,b: real):real;
begin
result := newton(Intervallhalbierung(a,b),10);
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, b, x1, x2, y1, y2, Schrittweite: real;
begin
a := -10;
b := 10;
Schrittweite := 1/10;
x1 := a;
y1 := f(x1);
memo1.Lines.Text := 'Nullstellen im Intervall ['+floatToStr(a)+';'+
FloatToStr(b)+']';
while x1 < b do Begin
x2 := x1 + Schrittweite;
y2 := f(x2);
if (y1 <= 0 ) and (y2 >= 0) or (y1 >=0 ) and (y2 <= 0) then
memo1.Lines.Add(floatToStr(nullstelleZwischen(x1,x2)));
x1 := x2;
y1 := y2;
End;
end;
Beispiel 13.5: Wie kann ich alle Dateien, die auf einem Datenträger
sind erfassen? Dateien können direkt auf dem Datenträger gespeichert sein, jedoch meistens sind sie in Verzeichnissen, in Unterverzeichnissen von Verzeichnissen u.s.w.
Hier lohnt sich das rekursive Durchsuchen. Das Programm dazu findest Du unter Fragen und Anworten
Ein weiteres Beispiel findest Du beim erweiterten euklidischen Algorithmus.
weitere Aufgaben zur Rekursion
14. Lektion: Arrays und Ordnungsalgorithmen
Ein Array ist eine indizierte Menge von Elementen desselben Typs. Zum Beispiel kann man in einem Stringarray die Namen der Schüler einer Klasse speichern.
var myarray: array[1..33] of string; //Deklaration eines statischen Arrays
begin
myarray[1] = 'Daniel';
myarray[2] = 'Jakob';
...
myarray[33] = 'Anna';
...
end;
I Statische Arrays und Bubblesort
Hinweis: Programm zur Veranschaulichung und zum Geschwindigkeitsvergleich von Sortieralgorithmen.Beispiel 14.1 Im Beispiel wird ein Array mit Zahlen gefüllt. Damit man auch etwas sieht, werden die Werte des Arrays in ein Memo geschrieben. Dann werden sie durcheinandergewirbelt (permutiert) und in ein zweites Memo geschrieben. Schließlich geordnet und in ein drittes Memo geschrieben.
const von = 5;
bis = 10;
var
Form1: TForm1;
aa: array[von .. bis] of integer; //globale Variablen
//dasselbe "aa: array[5 .. 10] of integer;
{Bei globalen Variablen verliert man leicht den Überblick.
(Delphi verwendet deshalb immer aussagekräftige Namen.)
Man kann dies ganz vermeiden, wenn man den Array als
Parameter an Prozeduren übergibt. Dann muss allerdings
der erste Index Null sein. (Siehe Ende des Kapitels.)}
implementation
{$R *.DFM}
procedure tausche(var a,b: integer);
var x: integer;
begin
x := a;
a := b;
b := x;
end;
procedure permutiere; //greift auf die globale Variable aa zu
var i:integer;
begin
for i := von to bis do
tausche(aa[i], aa[von + random(bis - von + 1]));
//kleinster wert von von + random(bis - von + 1])
//ist von + 0; größer wert von + bis -von = bis
end;
procedure bubblesort(n1,n2:integer);
//sortiert den globalen array von n1 bis n2
var i:integer;
fertig: Boolean;
begin
repeat
fertig:=true;
for i:=n1 to n2-1 do Begin
if aa[i] > aa[i+1] then BEgin
tausche(aa[i],aa[i+1]);
fertig:=false;
ENd;
End;
until fertig;
end;
procedure TForm1.Button1Click(Sender: TObject);
var k: integer;
begin
for k := von to bis do aa[k] := k;
memo1.Lines.Clear;
for k := von to bis do memo1.lines.Add(intTostr(aa[k]));
permutiere;
memo2.Lines.Clear;
for k := von to bis do memo2.lines.Add(intTostr(aa[k]));
bubblesort(von,bis);
memo3.Lines.Clear;
for k := von to bis do memo3.lines.Add(intTostr(aa[k]));
end;
Aufgabe 14.1 a) Schreibe ein Programm, das alle Namen die in
Memo1 stehen in Memo2 geordnet ausgegeben werden. Gehe davon aus,
dass in Memo1 zum Beispiel 20 Namen stehen. b) Schreibe ein Programm, das 6 Lottozahlen geordnet ausgibt.
Lösung
Beispiel 14.2 Arrays können auch Komponenten sein. Es werden 100 Labels zur Laufzeit erzeugt (genaueres Lektion 22), mit "1", "2", ... "100" beschriftet und gleichmäßig auf die Form1 verteilt. Im Vorgriff auf dynamische Arrays läuft diesmal der Index nicht von 1 bis 100 sondern von 0 bis 99.
procedure TForm1.Button1Click(Sender: TObject);
var b: array[0..99] of Tlabel;
k: integer;
begin
for k := 0 to 99 do Begin
b[k] := Tlabel.Create(Form1); //Zur Laufzeit erzeugen
b[k].Parent := Form1; //Labels müssen wissen, wohin sie gehören.
b[k].Top := (k div 10)*20;
b[k].Left := (k mod 10) *40;
b[k].Caption := IntToStr(k+1);
end;
showmessage('Ok');
for k := 0 to 99 do b[k].Free; //wieder freigeben (destroy)
end;
Überprüfe dein Können!
Uebungen 1. Block:
- Getestet wird, ob Du folgende Begriffe verstanden hast:
- Funktion (auch einfache rekursive Funktionen),
- Prozedur (mit der Bedutung von Wert- und Variablenparameter)
- Statische Arrays
- Bubblesort
- Natürlich auch Bedingungen, Schleifen und Wiederholungen u.s.w.
function test1(a,b: integer): integer;
begin
if a > 0 then result := a else
if b > 0 then result := b else result := 0;
end;
procedure test2(a,b:integer; var x:integer);
begin
if a > b then x := a else x := b;
end;
procedure TForm1.Button1Click(Sender: TObject);
var ergebnis: integer;
begin
ergebnis := test1(4,3);
memo1.Lines.Add('1. a) ' + inttostr(ergebnis));
ergebnis := test1(-4,-3);
memo1.Lines.Add(' b) ' + inttostr(ergebnis));
memo1.Lines.Add(' c) ' + inttostr(test1(-4,9)));
test2(4,3,ergebnis);
memo1.Lines.Add(' d) ' + inttostr(ergebnis));
test2(-4, 3,ergebnis);
memo1.Lines.Add(' e) ' + inttostr(ergebnis));
test2(-4, -3,ergebnis);
memo1.Lines.Add(' f) ' + inttostr(ergebnis));
end;
Aufgabe 14.u2 Was berechnet (Rechenausdruck genügt)
die folgende Funktion beim Aufruf von
a) f(3,2) b) f(2,3) c) f(5,10); d) f(0.75,200);
function f(x: real; n: integer): real;
begin
result := 1;
while n > 0 do Begin
result := result*x;
n := n - 1;
End;
end;
Aufgabe 14u3 Was berechnet (Rechenausdruck genügt)
die folgende Funktion beim Aufruf von
a) f(2) b) f(3) c) f(5); d) f(100);
function f(n: integer): real;
begin
if n = 1 then result := 1
else result := f(n-1)/n;
end;
Aufgabe 14u4 Die Oberfläche 0 und das Volumen V eines senkrechten Kreiskegels mit dem Radius r und der Höhe h berechnet sich zu
—————
/2 2
s =\/h + r
O = Pi*r*(s+r)
1 2
V = -Pi*r *h
3
Schreibe eine Prozedur "procedure kegel(...)" mit den "Eingangsvariablen" r und h und den "Ausgangsvariablen" O und V,
die die Oberfläche und das Volumen nach diesen Formeln berechnet.
Ergänze dann das folgende "Hauptprogramm" sinnvoll: procedure TForm1.Button1Click(Sender: TObject); var radius, hoehe, oberflaeche, volumen: real; begin radius := 5; hoehe := 10; //Berechnung der Oberfläche und des Volumens //showmessage ... oberfläche und Volumen end;
Aufgabe 14u5 Ein array sei als globale Variable folgendermassen deklariert:
var aa: array[1..50] of real;a) Schreibe eine Prozedur "procedure fuelle;", die aa mit ziemlich willkürlichen Zahlen füllt Es soll dabei das Körpergewicht von 50 Männern simuliert werden.
b) Schreibe dann eine Prozedur, die den Array aa so sortiert, dass die größte Zahl nach
Lösungen
Uebungen 2. Block (Diesselben Vorraussetzungen wie erster Block)
Aufgabe 14.uu1a) Was gibt das folgende Programm aus?
b) Ersetze die Prozedur durch eine Funktion. Wie ändert sich dann das Hauptprogramm ...Button1Click ...?
procedure oberstufeneu(p,m:real; var note:integer);
var n: real;
begin
p := p * 60 / m;
//Gute Schüler werden noch besser
if p > 56 then n := 15 else
if p > 55 then n := 14 else
//Hauptformel
if p > 23 then n := (p - 12) / 3 else
//Nicht so gute Schüler werden noch schlechter
if p > 22 then n := 4 else
if p > 18 then n := 3 else
if p > 14 then n := 2 else
if p > 10 then n := 1 else
n := 0;
note := trunc(n); //trunc rundet ab. z.B. trunc(4.99)=4
end;
procedure TForm1.Button1Click(Sender: TObject);
var max: real;
note: integer;
begin
max := 30; //Maximale Punktezahl der Klassenarbeit
oberstufeneu(7,max,note);
showmessage('Ronald erhält ' + inttostr(note) + ' Notenpunkte');
oberstufeneu(14,max,note);
showmessage('Gerhard erhält ' + inttostr(note) + ' Notenpunkte');
oberstufeneu(27,max,note);
showmessage('Joschka erhält ' + inttostr(note) + ' Notenpunkte');
end;
Aufgabe 14.uu2
a) Was berechnet folgendes Programm ?
b) Schreibe die Funktion so um, dass f(n)=1^2*2^2*3^2*...*n^2 wird.
function f(n: integer): real;
var k,a: integer;
begin
result := 0;
for k := 1 to n do Begin
a := k*k;
result := result + 1/a;
End;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
showmessage('f(2) = ' +floattoStr(f(2)) + #13+ //#13 "Neue Zeile!"
'f(4) = ' +floattoStr(f(4)) + #13+
'f(100) = ' +floattoStr(f(100)) + #13+
'f(0) = ' +floattoStr(f(0)) + #13+
'f(-2) = ' +floattoStr(f(-2)));
end;
Aufgabe 14.uu3
Schreibe ein Programm "Procedure quadrgl(a,b,c:real; var n: integer;
var x1,x2): real), das die Lösungen
x1,2 = (-b ± sqrt(d))/(2·a) der quadratischen Gleichung ax2 + bx +c = 0 ausgibt,
wobei d = b2 - 4·a·c ist.
Aufgabe 14.uu4 Formuliere die Funktionen f und g in Delphi (n: Integer)
1 1 1
a) Die Funktion f(n) soll 1 + - + - + ... + - berechnen.
2 3 n
1 3 5 2n-1
b) Die Funktion g(n) soll -·-·- · ... · ————
2 4 6 2n
berechnen.
Aufgabe 14.uu5 Was macht folgende Methode?
procedure TForm1.fuelleMemo(n:integer);
begin
memo1.Clear;
while memo1.Lines.Count <= n do
memo1.lines.add(chr(65+random(25)) + chr(65+random(25)) + chr(65+random(25)));
end;
Hinweis: chr(65) = 'A' chr(66) = 'B' u.s.w.
In Memo1 stehen 100 Namen.
Diese sollen in ein array gelesen werden, dort geordnet und in Memo2
geschrieben werden.
Lösungen
Uebungen 3. Block (Anspruchsvoller)
- Voraussetzungen
- Funktion (auch rekursive Funktionen bis mathematischer Parser)
- Prozeduren
- Statische Arrays
- Bubblesort
- Instanzen zur Laufzeit erzeugen)
function f(n: integer): real;
begin
//showmessage(intToStr(n));
if n <=1 then result := 0 else
if n mod 2 = 0 then result := f(n-1) + 1/n
else result := f(n-1) - 1/n
end;
a) Was wird bei f(10) berechnet? (Rechenausdruck genügt). b) Was wird bei f(-1) berechnet?
c) Schreibe dazu ein Hauptprogramm "procedure TForm1.Button1Click...", das eine Wertetafel für f(n) (n = 1,2,3, ... 10) ausgibt.
d) Im Programm werden die "//"-Zeichen entfernt. Wie oft erscheint beim Aufruf von f(10) das Meldungsfenster von "showmessage"?
Lösung
Aufgabe 14.z2 Betrachte folgende Funktion f!
function f(n: integer): real;
begin
//showmessage(intToStr(n));
if n=1 then result :=2 else
result := f(n-1)*f(n-1)
end;
a) Was wird bei f(10) berechnet? (Recheausdruck genügt). b) Was wird bei f(-1) berechnet?
c) Im Programm werden die "//"-Zeichen entfernt. Wie oft erscheint beim Aufruf von f(10) das Meldungsfenster von "showmessage" (Größenordnung genügt)?
d) Schreibe die Funktion f so um, dass die Effizienz verbessert wird. Es soll aber trotzdem noch eine rekursive Funktion sein.
Lösung
Bei den Aufgaben 14.z3 und 14.z5 wird vorausgesetzt, dass bekannt ist, wie Komponenten zur Laufzeit erzeugt werden (Lektion 22).
Aufgabe 14.z3 Schreibe ein Programm "procedure TForm1.Button1Click...", das 100 Editfenster, alle sichtbar (10 Reihen, 10 Spalten), auf dem Formular erzeugt. Die Editfenster sollen die Nummern 1 bis 100 tragen.
Zusatz: Vertausche anschließend den Inhalt des ersten, zweitem, dritten, ... Editfenster mit dem Inhalt eines zufällig ausgewählten weiteren Editfenster.
Lösung
Aufgabe 14.z4
Ein Array ist folgendermaßen als Variable definiert:
"var aa: array[0 .. 99] of integer;"
Schreibe eine Prozedur, die in aa[0], aa[1], ... und aa[99]
Zufallszahlen schreibt und anschließend dieses Array ordnet.
Dabei soll in aa[0] der größte Wert, in aa[1] der zweitgrößte Wert
u.s.w. stehen. Lösung
Aufgabe 14.z5
In einem Edit-Array stehen 100 verschiedene Zahlen zwischen 1 und 1000 zufällig verteilt. Das Array ist folgendermaßen als globale Variable definiert:
"var ee: array[0 .. 99] of Tedit;"
Schreibe eine Prozedur, die die 10 Editifelder rot färbt
die die höchsten Nummern tragen. Hinweis: "ee[0].color := clred" färbt ee[0] rot.
Lösung
Aufgabe 14.z6 Was ist ein mathematischer Parser und wie kann man ihn programmieren. Beschreibe in deinen Worten die Vorgehensweise.
Lösung
II Dynamische Arrays und Sortieren durch Mischen (Mergesort)
Seit Delphi 5 gibt es dynamische Arrays, d.h. die Feldgrenzen eines Arrays aa können zur Laufzeit mit setlength(aa,NeueLaenge) geändert werden. Zu Beachten ist:- Das erste Element ist immer aa[0]
- Das letzte Element ist immer aa[n-1], wobei n die Länge des Arrays ist: n := length(aa)
procedure TForm1.Button1Click(Sender: TObject);
var aa: array of string;
i: integer;
begin
setlength(aa,26); //dasselbe: setlength(aa,Ord('Z')-ord('A') + 1);
//Speicherplatz reserviert für aa[0], aa[1] .. aa[25]
for i := 0 to length(aa) - 1 do
//Achtung: letzter Speicherplatz bei length(aa) -1
aa[i] := char(65 + i) + char(65 + i);
for i := 0 to length(aa) - 1 do showmessage(aa[i]);
end;
Beispiel 14.4 Dasselbe Programm wie in Aufgabe 14.1. Namen, die ungeordnet in Memo1 stehen, sollen in ein Array eingelesen und geordnet werden und in Memo2 ausgegeben werden.
Unterschied:
- Es wird ein dynamische Array verwendet.
- Das Array wird nicht global deklariert, sondern als Parameter übergeben.
- Das array wird als "type Tstringarray = array of string" deklariert. Dies ist die beste Methode, wenn ein Array als Parameter einer Prozedur oder als result eine Funktion verwendet wird.
type Tstringarray = array of String; // Eigene Type-Deklarationen vor ...
var //... diese beiden Zeilen, die Delphi ...
Form1: TForm1; //... schreibt, einfügen
...
procedure tausche(var a,b: string);
var x: string;
begin
x := a;
a := b;
b := x;
end;
procedure bubblesort(var aa: Tstringarray); //statt aa: array of string
var i:integer;
fertig: Boolean;
begin
repeat
fertig:=true;
for i:=0 to length(aa) - 2 do Begin
if aa[i] > aa[i+1] then BEgin
tausche(aa[i],aa[i+1]);
fertig:=false;
ENd;
End;
until fertig;
end;
procedure TForm1.Button1Click(Sender: TObject);
var k: integer;
aa: Tstringarray; //statt aa: array of string;
begin
setlength(aa, memo1.lines.count);
for k := 0 to length(aa) - 1 do aa[k] := memo1.Lines[k];
bubblesort(aa);
memo2.Lines.Clear;
for k := 0 to length(aa) - 1 do memo2.lines.Add(aa[k]);
end;
Aufgabe 14.2 (Zahlen durcheinanderwirbeln und wieder ordnen.)
Formuliere Beispiel 14.1 so um, dass dynamische Arrays verwendet werden. Lösung
Beispiel 14.5 (Beispiel 14.2 auf dynamische Array abgewandelt.) Es werden 100 Labels zur Laufzeit erzeugt (genaueres Lektion 22), mit "1", "2", ... "100" beschriftet und gleichmäßig auf die Form1 verteilt.
procedure TForm1.Button1Click(Sender: TObject);
var b: array of Tlabel;
k: integer;
begin
setlength(b,100);
for k := 0 to length(b) - 1 do Begin
b[k] := Tlabel.Create(Form1); //Zur Laufzeit erzeugen
b[k].Parent := Form1; //Labels müssen wissen, wohin sie gehören.
b[k].Top := (k div 10)*20;
b[k].Left := (k mod 10) *40;
b[k].Caption := IntToStr(k+1);
end;
showmessage('Ok');
for k := 0 to length(b) - 1 do b[k].Free; //wieder freigeben (destroy)
end;
-
Aufgabe 14.3
Das Sieb des Eratosthenes zur Bestimmung aller Primzahlen funktioniert folgendermaßen: - Man schreibt alle Zahlen von 2 bis zum Beispiel n=1000 auf.
- Anschließend streicht man alle Vielfachen von 2 aus, nämlich 4,6,8,10,12,14,..., 1000
- dann alle Vielfachen von 3, nämlich 6,9,12,15,18 ..., 999
- (die Vielfachen von 4 braucht man nicht mehr durchstreichen, da alle geraden Zahlen bereits gestrichen sind)
- dann streicht man alle Vielfachen von 5, 7, 11 ,13 , ..., bis round(srt(1000))
- Übrig blieben nur die Primzahlen bis 1000
- Schreibe ein passendes Programm dazu!
Simuliert wird dies mit einem array aa of boolean. aa[k] := true bedeutet: Zahl steht noch da. aa[k] := false bedeutet: Zahl ist durchgestrichen (keine Primzahl).
Eratosthenes, geb. um 284 v. Chr., war ein Universalgelehrter. Von Athen holte in Ptolemaios III, Herrscher von Ägypten, nach Alexandria, wo er die dortige riesige wissenschaftliche Bibliothek leitete. Er starb 80jährig hochangesehen.
Aufgabe 14.4
In einer Textdatei stehen die Daten der Mitglieder eines Vereins in folgender Struktur:
Beispiel: (Vornamen ab 15. Stelle) Wöhl Alexandra Sabrina Reiser Inken Susanne Hertkorn Melanie Faigle Sandro Zorell Adrian Frank Lutz Katjenka Christina Bauer Tobias Maximilian Sinn ClaudiaDie Daten können nach folgender Prozedur mit Hilfe der Dialogkomponente opendialog1 in memo1 und anschließend in den dynamischen array daten eingelesen werden.
procedure TForm1.Button1Click(Sender: TObject);
var pfad: String;
k: integer;
begin
if opendialog1.Execute then
pfad := opendialog1.FileName;
memo1.Lines.LoadFromFile(pfad);
// Gegestück mit savedialog1: memo1.Lines.SaveToFile(pfad);
Anzahl := memo1.lines.Count;
setlength(daten,Anzahl);
for k := 0 to Anzahl-1 do
daten[k] := memo1.lines[k];
end;
Ordne die Datei
a) Nach Nachnamen b) Nach Vornamen
und schreibe sie in ein memo2!
Lösung
Sortieren durch Mischen
Die Zeit zum Sortieren wächst bei Bubblesort im Quadrat, d.h. Für die doppelte, dreifache ... Anzahl benötigt man, die vierfache, neunfache ... Zeit. Man sagt: Bubblesort ist von der Größenordnung O(n2).Wir kommen nun zu einem Sortierverfahren, das von der Größenordnung O(n·lb(n)) ist, wobei lb der Logarithmus zur Basis 2 ist. Zum Beispiel lb(8)=3, lb(1024)=10.
Vergleichen wir die beiden Größenordnungen, sehen wir den enormen Vorteil.
| n | n2 | n·lb(n) |
| 8 | 64 | 24 |
| 103 | 106 | 104 |
| 106 | 1012 | 20·106 |
Sortieren durch Mischen bedeutet im ersten Schritt (Beispiel 14.7): Man teilt den Stapel in zwei Teile, sortiert jede Hälfte extra und mischt sie dann geordnet zusammen.
Sortieren durch Mischen bedeutet im zweiten Schritt (Aufgabe 14.5): Man teilt den Stapel in vier Teile, sortiert jedes Viertel extra, mischt dann die ersten zwei und die letzten zwei und schließlich die sich ergebenden zwei Stapel zusammen.
Sortieren durch Mischen bedeutet im endgültigen Schritt (Aufgabe 14.6): Man halbiert die Stapel (rekursiv) solange, bis nur noch ein Element übrigbleibt (was natürlich gar nicht mehr sortiert werden muss) und mischt die Stapel dann geordnet zusammen.
Beispiel 14.7: Zwei Hälften werden mit Bubblesort geordnet und dann geordnet zusammengemischt.
Hinweis: Das Feld ist nun lokal definiert und wird als Parameter an die Ordnungsfunktion übergeben. So ist diese Funktion für jedes Array brauchbar. Mehrfache indizierte Araays müssen dann allerdings als Typ deklariert werden. (Siehe Lektion 15: Lösen von linearen Gleichungssystemen.)
procedure tausche(var a,b:real);
var x:real;
begin
x:=a;
a:=b;
b:=x;
end;
//Noch muss ein Teil sortiert werden. Primitv mit Bubblesort
procedure bubblesort(var aa:array of real; n1,n2:integer); //sortiert von n1 bis n2
var i:integer;
fertig: Boolean;
begin
repeat
fertig:=true;
for i:=n1 to n2-1 do Begin
if aa[i] > aa[i+1] then BEgin
tausche(aa[i],aa[i+1]);
fertig:=false;
ENd;
End;
until fertig;
end;
//Die folgende Prozedur bleibt beim rekursiven Programmieren übrig
procedure Einsortieren(var aa:array of real; n1,m,n2:integer);
//aa[n1]<=aa[n1+1] <=..<=aa[m] aa[m+1]<=aa[m+2]<=...<=aa[n2]
// i1——————————————————> i2——————————————————————>
// k—————————— füllt Hilfsfeld———————————————————————>
var i1,i2,k,n:integer;
hilf: array of real;
begin
n:=n2-n1+1; //Anzahl von aa[n1] ... aa[n2]
setlength(hilf,n); //Platz für hilf[0] ... hilf[n-1]
i1:=n1;
i2:=m+1;
for k:=0 to n-1 do //i1>m und i2>n2 auch abfangen!
if (i1>m) or ((i2<=n2) and (aa[i1]>aa[i2])) then Begin
hilf[k]:=aa[i2];
inc(i2);
End else Begin
hilf[k]:=aa[i1];
inc(i1);
End;
for k:=0 to n-1 do aa[n1+k]:=hilf[k];
end;
procedure zeige(mm:Tmemo; aa:array of real);
var i:integer;
begin
mm.Lines.Clear;
for i:=0 to length(aa)-1 do mm.Lines.Add(FloatToStr(aa[i]));
end;
procedure sortieren(var aa:array of real);
var n,mitte:integer;
begin
n:=length(aa); //z.B. n=10
mitte:=n div 2; //z.B. mitte:=5
bubblesort(aa,0,mitte-1); //ordnen von 0 bis 4 (5 Elemente)
bubblesort(aa,mitte,n-1); //Ordnen von 5 bis 9 (5 Elemente)
//Zu Testzwecken
zeige(form1.memo2,aa);
Einsortieren(aa,0,mitte-1,n-1);
end;
procedure TForm1.BFuellenClick(Sender: TObject);//Button1 umbenannt
var i,anzahl:integer;
aa:array of real;
begin
anzahl:=strToInt(EAnzahl.text);
setlength(aa,anzahl);
for i:=0 to Anzahl-1 do aa[i]:=i+1;
//Durcheinanderwirbeln
randomize;
for i:=0 to Anzahl-1 do tausche(aa[i],aa[random(Anzahl)]);
zeige(memo1,aa);
end;
procedure TForm1.BOrdnenClick(Sender: TObject); //button2 umbenannt
var aa:array of real;
n,i:integer;
begin
n:=strToInt(EAnzahl.text);
setlength(aa,n); //n Plätze für aa[0] bis aa[n-1] reserviert
for i:=0 to n-1 do aa[i]:=StrToFloat(memo1.lines[i]);
sortieren(aa);
zeige(memo3,aa);
end;
Aufgabe 14.5: Vier Hälften werden mit Bubblesort geordnet und dann
geordnet zusammengemischt. Verwende die Prozeduren von Beispiel 14.7. Lösung
Aufgabe 14.6:Sortiere einen Stapel durch Einsortieren rekursiv mit einer Prozedur sortieren(aa,n1,n2), die den array vom Index n1 bis zum Index n2 folgendermaßen sortiert:
Wenn n1 = n2 ist, tue nichts. Sonst:
Bestimme die Mitte m von n1 und n2.
Sortiere den Stapel vom Index n1 bis m.
Sortiere den Stapel vom Index m+1 bis n2.
Mische die beiden Stapel geordnet zusammen.
Lösung
