6. Lektion: Strukturiertes Programmieren (Einstieg)
Pascalfunktionen (1.Teil)
Die Funktion bei den Wertetafeln wollen wir nun außerhalb der button1click-Prozedur definieren. Das Programm lässt sich dann besser pflegen
Wichtig: Selbstdefinierte Funktionen müssen im Programm vor dem Aufruf stehen.
Hinweis: Viele Funktionen brauchen gar nicht mehr selbst definiert werden, da
sie schon als Standardfunktionen zur Verfügung stehen.
Klassische Mathematische Funktionen:
*) Betrag-, Quadrat- und und Wurzelfunktion
Abs(x):real (x:real) Beispiel: abs(-5) = 5
Die Funktion Abs(x) gibt den Absolutbetrag |x| zurück.
Sqr(x):real (x:real) Beispiel: sqr(-2.5) = 6.25
Die Funktion Sqr gibt das Quadrat eines Wertes zurück.
Sqrt(x):real (x:real) Beispiel: sqrt(2.25) = 1.5
Die Funktion Sqrt gibt die Quadratwurzel eines Wertes zurück.
*) Exponential- und Lorarithmusfunktione
Exp(x) = e^x (e hoch x) mit e=2.171828... Beispiel: exp(1) = 2.171828...
Ln(x):real
Die Funktion Ln gibt den natürlichen Logarithmus einer Zahl zurück.
Hinweis: Der Logarithmus zur Basis B ist dann ln(x)/ln(B)
Beispiel: lg(10000) = ln(10000)/ln(10) = 4
Und: Um a^x zu berechnen kann man für a>0 setzen: a^x = exp(ln(a)·x)
*) Trigonometrische Funktionen:
Sin(x):real (x:real im Bogenmaß) Beispiel: sin(30*Pi/180) = 0.5
Die Funktion Sin berechnet den Sinus eines Winkels.
Hinweis: sin(x*Pi/180) ist dann der sinus (x:Gradmaß)
Beachte: Pi=3,1415926535897932385 ist eine Konstante
Cos(x):real (x:Bogenmaß) Beispiel: cos(60*Pi/180) = 0.5
Die Funktion Cos berechnet den Cosinus eines Winkels.
Hinweis: cos(x*Pi/180) ist dann der Cosinus (x:Gradmaß)
tan(x):real (x:real im Bogenmaß) Beispiel: tan(45*Pi/180)
Die Funktion Tan berechnet den Tangens eines Winkels.
Hinweis: 1. tan(x*Pi/180) ist dann der Tangens (x:Gradmaß)
2. In der Standardversion von Delphi ist Tangens nicht verfügbar.
Kein Problem: Tan(x) = sin(x)/cos(x)
ArcTan(x):real (x:real) Beispiel:ArcTan(1) = Pi/4 (Hauptwert)
Die Funktion ArcTan berechnet den Arcustangens einer bestimmten Zahl.
ArcSin und ArcCos muss man sich selbst schreiben (Ist auch Sinnvoll, da nicht eindeutig!)
Delphifunktionen vom Typ Integer:
Round(x):integer (x:real) Round(4.5351) = 5 Round(4.45351) = 4
Die Funktion Round rundet den Wert von x auf den nächsten Integer-Wert.
Trunc(x):Integer Beispiel: Trunc(4.983) = 4
Die Funktion Trunc konvertiert eine Gleitkommazahl in einen Integer-Wert.
Delphifunktionen vom Typ Real:
Frac(x): real (x:real) Beispiel: Frac(2.4578) = 0.458
Die Funktion Frac gibt den Nachkommaanteil einer Zahl zurück.
Int(x):real (x:real). Fast dasselbe trunc(x):integer
Die Funktion Int gibt den ganzzahligen Anteil einer Zahl zurück.
Beispiel: Int(4.899) = 4
Funktionen vom Typ String:
Copy(s,a,b);string (s:string a,b:integer) Beispiel: copy('abcde',2,3) = 'bcd'
Die Funktion Copy gibt einen Teilstring eines Strings zurück.
Length(s):integer (s:string) Beispiel: length('abcde') = 5
Die Funktion Length gibt die Anzahl der Zeichen eines String zurück.
Pos (a,b):integer (a,b:string) Beispiel: pos('ef','aebcdef') = 6
Die Funktion Pos gibt den Indexwert des ersten Zeichens von a innerhalb
zurück, der in dem String b vorkommt (sonst =0)
Chr(n):char (n:integer 0<=n<=255). Umkehrfunktion ist ord(n).
Die Funktion Chr gibt das Zeichen mit einem bestimmten ASCII-Wert zurück.
Beispiel: chr('a') = 97 chr('A') = 65
Ord(c):integer (c:char) Beispiel: ord(97) = 'a' ord(65) ='A'
Die Umkehrfunktion von chr(n)
Konvertierungsfunktionen:
StrToInt(s):integer (s: String)
StrToInt konvertiert einen String, der eine Integer repräsentiert,
in eine Zahl.
StrToFloat(s): real (s: String)
StrToFloat konvertiert einen bestimmten String in einen Gleitkommawert.
IntToStr(n): String (n:integer)
IntToStr konvertiert den Integer-Wert n in einen String.
FloatToStr(x): String (x:real)
FloatToStr konvertiert die Gleitkommazahl x in die entsprechende
String-Darstellung.
Weitere Funktionen:
Random(n):integer (n:integer) Beispiel: Wuerfelaugenzahl :=Random(6) + 1
Die Funktion Random erzeugt die Zufallszahl 0 oder höchstens n-1
Randomize sollte einmal im Programm aufgerufen werden, das Random(n) verwendet.
Randomize initialisiert den Zufallszahlengenerator mit einem zufälligen Wert.
formatfloat('
0.
',x) :string (x: real)
formatfloat konvertiert die Gleitkommazahl x in die entsprechende
String-Darstellung. Die Stringdarstellung ist - hier als Beispiel -
mit einer Null vor dem Komma und mit passenden Leerzeichen formatiert.
Aufgabe 6.1 Betrachte folgende Funktion: (Schau Dir dazu die Onlinehilfe zu round und abs an!)
function f(x: real):real;
begin
result := round(abs(1000*x))/1000;
if x < 0 then result := -result;
end;
Was ist
a) f(25.45778)
b) f(-35,4445)
c) f(0.00005) ?
c) allgemein f(x) ?
Lösung
Nun wird am Beispiel gezeigt, wie mit einer selbst definierten Funktion x ——> f(x) gerechnet wird.
Beispiel 6.1 a) Berechnung von f(3) und f(2.1345) für f(x)= 1/3x^3 - 3x
function f(x:real):real; //Die eigenständig definierte Funktion
var y:real;
begin
y := 1/3*x*x*x - 3*x; //result ist der Rückgabewert
result := y; //Version ohne "y" siehe unten
end;
procedure TForm1.Button1Click(Sender: TObject);
var a,b: real;
begin
a := f(3);
b := f(- 2.1345);
showmessage('Der Wert der Funktion für x = 3 ist y= ' + FloatToStr(a));
showmessage('Der Wert der Funktion für x = -2,1345 ist = ' + FloatToStr(b));
end;
Beispiel 6.1 b) Wertetafel für f(x) = 1/3x^3 - 3x
function f(x:real):real;
begin
result := 1/3*x*x*x - 3*x;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x, x1, x2, s, y:real;
begin
x1 := -5; //Alternative: Einlesen von editx1
x2 := 5; //Alternative: Einlesen von editx2
s := 1/2; //Alternative: Einlesen von editx2
x := x1; //Anfangswert
memo1.Lines.clear;
while x <= x2 do Begin
y := f(x);
memo1.lines.Add(FloatToStr(x) + ' ' + FloatToStr(y));
x := x + s;
End;
end;
Aufgabe 6.2: Schreibe mit Hilfe einer Funktion eine Wertetafel
für f(α)=2*sin(α)+sin(2*α)
für α = -720°, ..., 0°, 30°, 60°, .. 720°
Lösung
Beispiel 6.2 a) Die Fakultät n! = 1*2*...*n wird als Funktion definiert, auf "Buttonklick" dann 10! ausgegeben. function fakultaet(n:integer):real; //n: Eingangsparameter var k: integer; p: integer; //k und p: lokale Variable begin p := 1; //Version ohne "p" siehe unten for k := 1 to n do p := p*k; //siehe Produkt result := p; //result ist der Rückgabewert end; procedure TForm1.Button1Click(Sender: TObject); begin showmessage(FloatToStr(fakultaet(10))); //Zeigt: 10! = 3 628 800 end; {Bemerkung: Da Fakultaet(17) schon zu groß für den Typ Integer wird, ist hier der Rückgabewert von Fakultaet vom Typ real} Beispiel 6.2 b) (rekursiv siehe Beispiel 10.1)Funktionen mit zwei oder mehr Eingangsparametern sind möglich. Zum Beispiel die bei der Binominialverteilung wichtige Funktion:
Die Fakultät n! = 1*2*...*n wird als Funktion definiert. Auf "Buttonklick" dann eine Wertetafel ausgedruckt. Bemerkung: Der Rückgabewert result darf wie eine lokale Variable verwendet werden. function fakultaet(n:integer):real; //Ohne lokale Variable p var k: integer; //k: lokale Variable begin result := 1; for k := 1 to n do result :=result*k; end; procedure TForm1.Button1Click(Sender: TObject); var i:integer; begin memo1.text := 'n fakultaet(n)'; for i := 1 to 100 do memo1.lines.add(IntToStr(i)+' '+ formatfloat('
',fakultaet(i))); end;
Aufgabe 6.3 a) Programmiere nuebk(n,k) ohne Fakultäte nach folgender Formel:n n! 49 "n über k". ( ) = ————————— . Zum Beispiel ( ) = 13 983 816 k k!·(n-k)! 6 Die Funktion in Delphi programmiert: function nuebk(n,k:integer):real; begin result := fakultaet(n)/(fakultaet(k)*fakultaet(n-k)) end;
Weitere Aufgaben zu Funktionen (mit Lösungen)n n·(n-1)·(n-2)·..·(n-k+1) ( ) = ———————————————————————— k 1 · 2 · 3 ... · k Hinweis: Hier kann der Ergebnistyp als integer deklariert werden. Die Division muss dann allerdings mit "div" (ganzzahlige Division) statt mit "/" durchgeführt werden. b) Drucke in ein Memofeld das Pascalsche Dreieck 1 Zeile 0: nuebk(0,0) 1 1 Zeile 1: nuebk(1,0) nuebk(1,1) 1 2 1 ... 1 3 3 1 1 4 6 4 1 Zeile 4: nuebk(4,0) nuebk(4,1)...nuebk(4,4) ... Lösung
Aufgabe 6.4: Schreibe eine Funktion hoch(x,n), die für natürliche Zahlen n den Wert y := yn ausgibt. Teste 210; 1,52 und 50! Lösung
7. Lektion: if .. then und if .. then .. else .. II. Teil
- Dazu:
- Die Ganzzahloperationen div und mod.
- and, or und not
- random(n)
- application.ProcessMessages
- sleep(1000)
- Der Befehl exit (siehe Besprechnung von Aufgabe 7.3)
- Die Eigenschaft PasswordChar eines Editfeldes.
Beispiel 7.1 bis 7.4 sind identisch mit Beispiel 3.1 bis 3.4.
Jetzt werden Bedingungen (1. Thema) und Schleifen (2.Thema) kombiniert (Wenn du dich in der Sonatenform auskennst, befinden wir uns nun in der Durchführung. Das ist bei einer Symphonie der ergreifendste Teil.).
Beispiel 7.5: Alle Teiler i der Zahl p=17017 sollen ausgegeben werden.
procedure TForm1.Button1Click(Sender: TObject);
var p,i:integer;
begin
p := 17017;
memo1.text := 'Teiler von ' + intToStr(p) + ':';
for i := 1 to round(sqrt(p)) do
if p mod i = 0 then
memo1.Lines.add(intToStr(i)+' '+intToStr(p div i));
end;
Beispiel für die hier verwendeten Operatoren div und mod:
17 : 5 = 3 Rest 2
Ganzahlig kann 17 nicht durch 5 dividiert werden, deshalb ist
17/5 als Gleitkommadivision bei Integer-Zahlen nicht erlaubt.
q := 17 div 5 ergibt q = 3 (div: Die ganzzahlige Division)
r := 17 mod 5 ergibt r = 2 (mod: Der Rest)
Somit: 17 = q*5 + r mit 0 <= r < 5
Allgemein: q := p div i ergibt den ganzzahligen Quotienten
r := p mod i ergibt den Rest
Somit: p = q*i + r mit 0 <= r < i, (p,q,r : Integer)
Und: Ist i ein Teiler von p, dann ist der Rest r = p mod i = 0
Wir verwenden hier einen Trick, um die Schleife
for i := 1 to p
drastisch verringern zu können. Wir geben gleichzeitig zum Teiler i den
korrespondierenden Teiler j = p/i aus. So braucht die Schleife nur bis
höchstens zur Quadratwurzel sqrt(q) von q laufen. Ist nämlich j ein Teiler von q mit j > sqrt(q), dann gibt es ein zugehöriges i mit p = i*j mit i < sqrt(q) (sonst wäre i*j > q).
Im folgendem Programm werden die 2-er Potenzen ausgegeben. Dazu wird
die Funktion hoch(x,n) = xn verwendet.
Beispiel 7.6: Wertetafel für
2-20, 2-19, ... 219, 220
Die Funktion hoch(x,n) wird jetzt auf negative Hochzahlen n
erweitert.
function hoch(x:real; n:integer):real; //x^n (x:real; n ganze Zahl)
var p:real;
i,nabs:integer;
begin
nabs := abs(n);
p :=1;
for i := 1 to nabs do p := p*x;
if n < 0 then result := 1/p else result := p;
//Beachte: x^(-n) = 1/x^n für n < 0
end;
procedure TForm1.Button1Click(Sender: TObject);
var n: integer;
y: real;
begin
memo1.lines.clear;
for n := -20 to 20 do Begin
y :=hoch(2,n);
memo1.Lines.Add(IntToStr(n)+ ' ' +
formatfloat('
0.
',y));
End;
end;
formatfloat('
0.
',y) gibt den Wert von
y formatiert aus: Eine Null vor dem Komma und mit passenden Leerzeichen.
- Aufgabe 7.2:
- Oft muß man Zahlenreihen so untereinander schreiben, dass das Komma immer an derselben Stelle steht.
- Schreibe deshalb eine Funktion, die mit Hilfe von
formatfloat('
0.
',x) eine Gletkommazahl in einen String umwandelt, der genau 11 Zeichen vor dem Komma hat. - Teste die Funktion mit einer Wertetafel.
- Hinweis:
- Das Komma findest du mit der Funktion pos(',',s). Achte darauf, dass Komma und zwei Nachkommastellen möglicherweise durch Leerzeichen "hinten" aufgefüllt werden müssen.
- Die Länge eines String s findest du mit der Funktion
length(s).
Achte darauf, dass der Gesamtstring 14 Zeichen haben muss und möglicherweise "vorne" mit Leerzeichen aufgefüllt werden muss. - Aufgabe 7.3:
- Schreibe eine Funktion IstPrimzahl(n), die für eine natürliche Zahl n true oder false ausgibt, je nachdem sie prim ist oder echte Teiler hat.
- Im Programm sollen dann alle Primzahlen bis 1000 in ein Memofeld geschrieben werden. Die Einer, Zehner, .. sollen dabei untereinander stehen.
- Aufgabe 7.4:
- Schreibe ein Programm zur Passwortabfrage.
- Hinweis:
- 1. Mit edit1.PasswordChar := '*' werden die Eingaben in edit1 unsichtbar.
- 2. Bei der Lösung findest du einen Hinweis, wie man die Passwortabfrage auf drei mal beschränken kannst (mit Hilfe einer globalen oder privaten Variablen.)
Nach if können auch mit and, or und not verknüpfte Wahrheitswerte stehen.
Sind a und b boolsche Variablen (also true oder false), dann gilt folgende Wahrheitstabelle. Der Vollständigkeit wird das hier nicht behandelte xor ("entweder-oder") mit erwähnt.
| Wahrheitstabelle nach Wittgenstein | |||||
|---|---|---|---|---|---|
| a | not a | b | a and b | a or b | a xor b |
| true | false | true | true | true | false |
| true | false | false | false | true | true |
| false | true | true | false | true | true |
| false | true | false | false | false | false |
- Merke:
- a and b ist nur true, wenn a true und b true
- a or b ist nur false , wenn a false und b false. Es handelt sich hier um das nicht ausschließende "oder" (lateinisch: vel) und nicht um "Entwerder-Oder" (lateinisch:"aut". In der Booleschen Algebra das exklusive oder "xor").
function f(a: boolean): string; // f=BooleanToString
begin
if a then result := ' true ' else
result := ' false ';
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, b :boolean;
begin
memo1.Font.Name := 'Courier New'; //gleicher Abstand
memo1.text := ' a b a and b a or b a xor b';
a := true; b := true;
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
a := true; b := false;
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
a := false; b := true;
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
a := false; b := false;
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
end;
Das folgende, elegantere Programm macht dasselbe. Dabei ändert b seinen
Wahrheitswert ständig, a nur jedes zweite Mal. Dann
würde es von vorne beginnen, wenn nicht nach fünf Zeilen Schluss wäre.
(Für dich eine gute Übung, das ausführlich nachzuvollziehen. Vielleicht
wird es für ich einfacher, wenn du "b" durch das äquivalente "b = true"
ersetzt. Denn ist "b" true, dann ist "b = true" natürlich auch
true und auch "(b = true) = true" u.s.w. Die Beteuerung
"Ich sag die Wahrheit" ist, logisch gesehen, überflüssig.)
function f(a: boolean): string; // f=BooleanToString
begin
if a then result := ' true ' else
result := ' false ';
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, b :boolean;
begin
memo1.Font.Name := 'Courier New'; //gleicher Abstand
memo1.wordwrap := false; //siehe Bemerkung unten
memo1.text := ' a b a and b a or b a xor b';
a := true; b := true;
repeat
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
b := not b;
if b then a := not a;
until memo1.lines.count >= 5;
end;
Bei diesem Programm zeigte sich wieder einmal die Tücke der Programmierung:
Beim ersten Test meines Programms fehlte die Zeile "memo1.wordwrap := false".
(Das bedeutet: Kein Zeilenumbruch, falls Zeile zu lang.)
Und: Der Abbruch der Repeat-Schleife war "until memo1.lines.count = 5".
Promt landete ich in einer Endlosschleife, weil mein Memo1 nicht
breit genug war und auf einmal eine Zeile durch zwei Zeilen ersetzt wurde.
Nach Zeilenlänge "4" kam nicht "5" sondern "6". Fatal! Deshalb noch die komponentenunabhängige Lösung ohne wordwrap. (Das sollte man immer anstreben. Dann ist die Übertragung in eine andere Programmiersprachen einfacher).
function f(a: boolean): string; // f=BooleanToString
begin
if a then result := ' true ' else
result := ' false ';
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, b :boolean;
k: integer;
begin
memo1.lines.clear:
memo1.lines.add := ' a b a and b a or b a xor b';
a := true; b := true;
k := 0;
repeat
memo1.lines.add(f(a) + f(b) + f(a and b) + f(a or b) + f(a xor b));
inc(k); //Dasselbe wie k := k + 1;
b := not b;
if b then a := not a;
until k = 5;
end;
Beispiel 7.7: In einer Schachtel befinden sich 15 blaue, grüne, rote und
gelbe Buntstifte, von jeder Farbe mindestens einer. Blaue Stifte sind am
meisten und grüne am wenigsten vorhanden.
Außerdem hat es gleichviele rote wie gelbe Stifte. Durch ein einfaches "brutales" Programm lassen sich alle Möglichkeiten ermitteln.
procedure TForm1.Button1Click(Sender: TObject);
var blau, gruen, rot, gelb: integer;
begin
memo1.Text := 'blau grün rot gelb';
for blau := 1 to 15 do
for gruen := 1 to 15 do
for rot := 1 to 15 do
for gelb := 1 to 15 do
if (blau > gruen) and
(blau > rot) and
(blau > gelb) and
(gruen < blau) {entbehrlich} and
(gruen < rot) and
(gruen < gelb) and
(rot = gelb) and
(blau + gruen + rot + gelb= 15) then
memo1.lines.add(IntToStr(blau)+ ' '
+ IntToStr(gruen) + ' '
+ IntToStr(rot) + ' '
+ IntToStr(gelb));
end;
Die Klammern in diesem
Beispiel sind unbedingt notwendig, da z.B. X and Y für
Integerzahlen X und Y (siehe Bitweise Operatoren)
Vorrang vor true and false hat.
Merke:
Bei and, or und not besser Klammern setzten.Zum Beispiel hat (2 < 3) and (-4 < -3) den Wahrheitswert true.
Dagegen erzeugt 2 < 3 and -4 < -3 einen Syntaxerror.
Beispiel 7.8: Drei Lottozahlen werden erzeugt
(erweiterbar auf 6 Lottozahlen plus Zufallszahl)
procedure TForm1.Button1Click(Sender: TObject);
var x1,x2,x3: integer;
begin
randomize;
x1 := random(49) + 1;
edit1.text := IntToStr(x1);
application.ProcessMessages; //Windows ändert sofort edit1
sleep(2000); // 2 Sekunden Geduld
x2 := x1;
while x2 = x1 do x2 := random(49) + 1;
edit1.text := edit1.text+' '+IntToStr(x2);
application.ProcessMessages;
sleep(2000);
x3 := x2;
while (x3 = x1) or (x3 = x2) do x3 := random(49) + 1;
edit1.text := edit1.text+' '+IntToStr(x3);
application.ProcessMessages;
sleep(2000);
end;
Beispiel 7.9: Umwandlung Dezimalzahl in roemische Zahl
 Programm dazu: siehe Downloadseite
Programm dazu: siehe Downloadseite
Der Algorithmus ist folgender: Beispiel 1964
1. Tausender verarbeiten 1000 = M 1964=M+964 (M+Rest)
Rest >=900? 900 = CM 1964=M+CM+64 (MCM+Rest)
Rest >=500? 500 = D
Rest >= 400? 400 = CD
2. Hunderter verarbeiten 100 = C
Rest >= 90? 90 = XC
Rest >= 50? 50 = L 1964=MCM+L+14
Rest >= 40? 40 = XL
3. Zehner verarbeiten 10 = X 1964=MCM+L+X+4
Rest >= 9? 9 = IX
Rest >=5? 5 = V
Rest >= 4? 4 = IV 1964=MCM+L+X+IV
4. Einer verarbeiten 1 = I
In Delphi "übersetzt" wird es etwas lang. Wenn du aber die "Tausender"
verstanden hast, ist der Rest wegen der Ähnlichkeit leicht.
Function roemisch(n: integer):string;
begin
result := '';
{——————— Tausender —————————}
while n >= 1000 do Begin //kann mehrmals vorkommen
result := result +'M';
n := n-1000;
End;
if n >= 900 then Begin //kann nur einmal vorkommen
result := result +'CM';
n := n-900;
End;
if n >= 500 then Begin
result := result +'D';
n := n-500;
End;
if n >= 400 then Begin
result := result +'CD';
n := n-400;
End;
{————————— Hunderter ——————————— }
while n >= 100 do Begin //kann mehrmals vorkommen
result := result +'C';
n := n-100;
End;
if n >= 90 then Begin
result := result +'XC';
n := n-90;
End;
if n >= 50 then Begin
result := result +'L';
n := n-50;
End;
if n >= 40 then Begin
result := result +'XL';
n := n-40;
End;
{——————— Zehner ———————————}
while n >= 10 do Begin
result := result +'X';
n := n-10;
End;
if n >= 9 then Begin
result := result +'IX';
n := n-9;
End;
if n >= 5 then Begin
result := result +'V';
n := n-5;
End;
if n >= 4 then Begin
result := result +'IV';
n := n-4;
End;
{ ——————————— Einer ——————————— }
while n >= 1 do Begin //kann mehrmals vorkommen
result := result +'I';
n := n-1;
End;
end;
Dieses Programm kürzer geschrieben findest du im Downloadverzeichnis
unter Umwandlung Dezimalzahl in römische Zahl
Aufgabe 7.5: Ineinandergeschachtelte if ... then-Anweisungen.
Was wird im folgendem Programm berechnet?
procedure TForm1.Button1Click(Sender: TObject);
var a,b,c :integer;
begin
for a := 0 to 1 do for b := 0 to 1 do Begin
if a = 0 then BEgin
if b = 0 then c := 2 else c := 3;
ENd else BEgin
if b = 0 then c := 5 else c := 7;
ENd;
memo1.lines.add('a='+IntToStr(a)+' b='+IntToStr(b)+
' c='+IntToStr(c));
End;
end;
Hinweis: Bei verschachtelten if ... then-Konstrukten ist Pascal zweideutig. Schreibe nie
if b0 then if b1 then s0 else s1sondern entweder
if b0 then Begin
if b1 then s0 else s1
End
oder
if b0 then Begin
if b1 then s0
End else s1
wobei b0,b1 Bedingungen und s0,s1 Anweisungen bedeuten sollen.
Lösung
Beispiel 7.10 Eingabefelder löschen bei Kreisberechnungen.
Setzte 4 Editfelder und 4 Buttons auf ein Formular. Im Objektispektor kannst du die Namen für die Editfelder umbenennen.
Nenne sie er, ed, eu und eA!
In den Eingabefeldern er für den Radius, ed für den Durchmesser, eu für den Umfang und eA für die Fläche des Kreises werden nach Eingabe einer Größe die anderen Größen berechnet. Sobald eine Eingabe erfolgt, werden die anderen Felder gelöscht. Schreibe die Ereignisprozedur OnKeyUp für er folgendermaßen:
procedure TForm1.erKeyUp(Sender: TObject; var Key: Word; Shift: TShiftState); begin if sender <> er then er.text := ''; if sender <> ed then ed.text := ''; if sender <> eu then eu.text := ''; if sender <> ea then ea.text := ''; end;Weise nun auch den Feldern ed, eu, eA im Objektinspektor unter "Ereignisse" dieselbe Ereignisprozedur OnKeyUp zu.
Jetzt ist klar: Der Text des Feldes, in dem die Eingabe erfolgt, wird nicht gelöscht, jedoch in allen anderen Editfeldern. Wird zum Beispiel gerade der Radius eingeben, ist Sender = er und er.text wird nicht auf '' gesetzt, aber alle anderen.
Aufgabe 7.6: Ergänze nun das Programm so, dass auf Klick auf einen Button aus dem Radius, auf Klick auf einen zweiten Button aus dem Durchmesser u.s.w. alle übrigen Größen berechnet werden.
Lösung
Beispiel 7.10 Zerlegung einer Zahl in ihre Primfaktoren.
Beispiel: 4004 zerlegt in seine Primfaktoren: 4004= 2·2·7·13
Verfahren: Wir dividieren 4004 nacheinander, auch mehrmals, durch 2,3,5, 7 ..., bis zum Schuß 1 dasteht.
Ein solches Verfahren nennt man auch Algorithmus. Präziser formuliert:
| Wiederhole... |
| Falls n durch i (i=2,3,5,7,...) dividiert werden kann, notiere i und ersetze n durch n/i. |
| ... bis n=1. |
| Die notierten i's sind die Faktoren der PFZ |
Bsp.: n=4004
i=2 n=2002
i=2 n=1001
i=7 n=143
i=11 n=13
i=13 n=1
Also: 4004=2*2*7*11*13
Eine Beschleunigung erreicht man durch folgende Überlegung:
Ist n=a·b so muss ein Faktor a oder b kleiner/gleich sqrt(n) sein.
(Widerspuchsbeweis: a > sqrt(n) und b > sqrt(n) = > a·b > n )
Man braucht also nur mögliche Faktoren i <= sqrt(n) betrachten. In Pascal:(rekursiv Beispiel 10.4)
function PFZ(n:integer):string; var i:integer; begin result:=''; i:=2; repeat while n mod i =0 do BEgin n:=n div i; if result <> '' then result:=result+'*'; //Das 1. Mal kein '*' result:=result+floatToStr(i); ENd; if i=2 then i:=i+1 else i:=i+2; //ungerade (eigentlich genügen Primzahlen) if i > trunc(sqrt(n)) then i:=n; //ohne diese Zeile:Kaffeepause! until n=1; if pos('*',result)=0 then result:='Primzahl'; end;
8. Lektion: Case .. of .. End
Dazu: Die Komponente RadiogroupViele ineinandergeschachtelte if .. then kann man ersetzten durch Case .. of .. else .. End.
Zum Beispiel kann man statt
if i = 1 then s := 'eins' else
if i = 2 then s := 'zwei' else
if i =3 then s := 'drei' else
s := 'viel'
schreiben
Case i of 1: s := 'eins';
2: s := 'zwei';
3: s := 'drei';
else s := 'viel';
End;
Beispiel 8.1: Hier wird dies demonstriert:
procedure TForm1.Button1Click(Sender: TObject);
var i : integer;
s : string;
begin
for i := 1 to 10 do Begin
CAse i of 1: s := 'eins';
2: s := 'zwei';
3: s := 'drei';
else s := 'viel';
ENd;
showmessage(intToStr(i) + ' = ' + s);
End;
end;
Dasselbe ohne else:
procedure TForm1.Button1Click(Sender: TObject);
var i : integer;
s : string;
begin
for i := 1 to 10 do Begin
s := 'viel';
CAse i of 1: s := 'eins';
2: s := 'zwei';
3: s := 'drei';
ENd;
showmessage(intToStr(i) + ' = ' + s);
End;
end;
Beispiel 8.2:
Du benötigst hier radiogroup1 aus der Standardkomponentenleiste.
Bei einer Radiogroup kann der Benutzer aus
einer Gruppe von Feldern genau eines auswählen.
Aktiviere radiogroup1 und doppelklicke im
Objektinspektor bei items auf "..." und schreibe
in den sich nun öffnenden String-Listen-Editor
rot
blau
grün
gelb
schwarz
weiß
Wird jetzt auf der Radiogrup eine Farbe gewählt, soll
das Fenster die entsprechnede Farbe enthalten:
procedure TForm1.RadioGroup1Click(Sender: TObject);
begin
Case radiogroup1.ItemIndex of 0 : color := clred;
1 : color := clblue;
2 : color := clgreen;
3 : color := clyellow;
4 : color := clblack;
5 : color := clwhite;
End;
//Nur zur Demonstration
for i :=0 to radiogroup1.Items.Count -1 do
showmessage(IntToStr(i) + '=' +radiogroup1.items[i]);
end;
Beachte: Die Feldelemente heißen items.
Die Anzahl der Elemente ist radiogroup1.Items.Count.
Die Feldelemente (Items) der Radiogroup werden von
0 an durchnummeriert bis radiogroup1.Items.Count -1.
(In der Informatik fängt man häufig bei 0 an zu zählen!)
Die Eigenschaft itemindex ist die Nummer des
ausgewählten Elements.
Für den Fachmann:clred u.s.w. sind vordefinierte Konstanten.
Genauer: In der unit graphics wird definiert
clRed = TColor($0000FF)
clBlue = TColor($FF0000)
clLime = TColor($00FF00)
(Daraus kann man alle Farben mischen)
clBlack = TColor($000000) (Kein Farbpixel wird aktiviert)
clWhite = TColor($FFFFFF) (Alle drei Farbpixel)
Aufgabe 8.1:
Unter folgenden Bedingungen zahlt ein Betrieb an seine Mitarbeiter
eine Jahresendprämie:
Betriebszugehörigkeit weniger als ein Jahr : keine Prämie
Betriebszugehörigkeit ein Jahr aber weniger als 5 Jahre: 200 EUR
Betriebszugehörigkeit 5 Jahre aber weniger als 10 Jahre: 400 EUR
Betriebszugehörigkeit 10 Jahre und mehr : 800 EUR
Schreibe dazu ein passendes Programm und verwende dabei "Case"!
Aufgabe 8.2:
Der Fahrkartenautomat gibt aus
Einzeltageskarten für 1 Zone zu EUR 2,00
Gruppentageskarten für 1 Zone zu EUR 3,00
Einzeltageskarten für 3 Zonen zu EUR 5,00
Gruppentageskarten für 3 Zonen zu EUR 8,00
Einzeltageskarten für 6 Zonen zu EUR 9,00
Gruppentageskarten für 6 Zonen zu EUR 14,00
Simuliere den Automaten!
Aufgabe 8.3:
Plaztiere ein Spinedit- und ein Editfeld auf Dein Formular.
Nach Eingabe der Punktzahl im Spineditfeld soll die Note in Worten
im Editfeld erscheinen. Zum Beispiel:
Notenpunkte Note
11 gut
Schreibe dazu ein Programm.
Aufgabe 8.4:
Oft werden Prüfsummen folgendermaßen gebildet:
Multipliziere die erste Ziffer mit 7,
die zweite mit 3,
die dritte mit 1,
die vierte wieder mit 7,
u.s.w.
und addiere alle Summandden.
Die Prüfziffer ist dann die letzte Ziffer dieser Summe.
z.B. Prüfsumme von 861214 = 8·7 + 6·3 + 1·1 + 2·7 + 1·3 + 4·1 = 96
Prüfziffer = 6
Schreibe eine Funktion unter Verwendung von Case, die die Prüfsumme ermittelt.
Lösung
Überprüfe dein Können!
Aufgabe 8.5 Was passiert bei folgendem Programm? Gib insbesondere an, was im Memo1 steht! (Ausrechnen, z.B. 5/2*Pi=7,85 nicht notwendig!)
a) function flaeche(art: string; r: real): real;
begin
if art = 'Kreis' then result := Pi*r*r else
if art = 'Quadrat' then result := r*r else
if art = 'Kugel' then result := 4/3*Pi*r*r*r
else Begin
showmessage('Unbekanntes Objekt');
result := 0;
End;
end;
procedure TForm1.Button1Click(Sender: TObject);
var a, r, y: real;
begin
r := 5;
y := flaeche('Kreis',r);
memo1.lines.Add('Kreisfläche (r=5) = ' + FloatToStr(y));
a := 3;
y := flaeche('Quadrat',a);
memo1.lines.Add('Quadrat (a=3) = ' + FloatToStr(y));
a := 10;
y := flaeche('Dreieck',a);
memo1.lines.Add('gleichseitiges Dreieck (a=10) = ' + FloatToStr(y));
end;
b) function f(x: real): real;
var p, q: real;
begin
p := 0;
if x < 0 then p:= 2*x;
if x > 0 then q := x/2 else q := 0;
result := p + q;
end;
procedure TForm1.Button1Click(Sender: TObject);
var i: integer;
begin
for i := - 2 to 2 do
memo1.lines.add(IntToStr(i)+ ' '+ floatToStr(f(i)));
end;
c) function g(a,b: real): real;
begin
if a > 0 then result := 2*a + 3*b
else result := 2*a - 3*b;
end;
procedure TForm1.Button1Click(Sender: TObject);
var i:integer;
begin
i := -4;
repeat
memo1.lines.add(IntToStr(i)+ ' '+ floatToStr(g(i,2*i)));
i := i+2;
until i = 4;
end;
d) function h(x: integer): real;
var p, q: real;
begin
p := 1;
q := 1;
while q <= x do Begin
p := p*q;
q := q + 1;
End;
result := p;
end;
procedure TForm1.Button1Click(Sender: TObject);
var a: integer;
begin
a := 0;
while a <= 5 do Begin
memo1.lines.add(IntToStr(a)+ ' '+ floatToStr(h(a)));
a := a + 1;
End;
end;
Aufgabe 8.6 Schreibe ein Programm "Procedure ... Button1Click ..",
das die Lösungen x1,2 = (-b ± sqrt(d))/(2·a)
der quadratischen Gleichung ax2 + bx +c = 0 ausgibt,
wobei d = b2 - 4·a·c ist. In 3 Editfeldern soll die Eingabe a, b, c und in 2 Editfeldern die Ausgabe x1,2 stehen. Etwa so:
edit1 edit2 edit3
a b c
edit4 edit5
x1 x2
Das zusätzlich Besondere bei Deinem Programm soll sein:
Zwei Lösungen (d > 0): zusätzlich edit5.show Eine Lösung (d = 0): edit5.hide Keine Lösung (d < 0): edit4.text ='keine Lösung' edit5.hideAufgabe 8.7 Im Edit1-Feld soll die Punktzahl eingeben werden, im Edit2-Feld soll dann die zugehörige Note in Buchstaben stehen. Schreibe unter Verwendung von Case das zugehörige Programm!
Zur Erinnerung: 0 -> ung; 1, 2, 3 -> mgh; 4, 5, 6 -> ausr;
7,8,9 -> bfr; 10,11,12 -> gut; 13,14,15 -> sgt
Aufgabe 8.8 Formuliere die Funktionen f und g in Delphi (n: Integer)
Aufgabe 8.9 Was wird bei folgendem Programm ins Memo geschrieben?1 1 1 a) Die Funktion f(n) soll 1 + - + - + ... + - berechnen. 2 3 n 1 3 5 2n-1 b) Die Funktion g(n) soll -·-·- · ... · ———— 2 4 6 2n berechnen.
procedure TForm1.Button1Click(Sender: TObject);
var a, b, q, r, a1:integer;
begin
a := 416;
b := 160;
repeat
q:= a div b;
r:= a mod b;
a1 := q*b + r;
memo1.Lines.Add(' a = ' + intToStr(a) +
' q = ' + intToStr(q) +
' r = ' + intToStr(r) +
' a1 = ' + intToStr(a1));
a:=b;
b:=r;
until r = 0;
end;
Lösungen von Aufgaben 8.5 bis 8.9 (Haus-)Aufgabe 8.10 Schreibe ein Simulationsprogramm. Verwende dazu die Komponente Timer. Ein Tag soll in 500 ms entsprechen.
//Wichtig: Kommentiere das Programm ausführlich.
Eugen hat eine Aktie A im Wert von 1000 EUR. Josef hat 1000 EUR bar.
Täglich wechselt die Aktie den Besitzer. Der Wert der Aktie kann
täglich um maximal p% nach oben oder unten schwanken (random).
Wie viel besitzt jeder nach einem Tag, nach zwei, drei ... Tagen?
9. Lektion: Algorithmen
Die Informatik beschäftigt sich mit dem Auffinden von Lösungen von Problemen. Genauer befasst sie sich mit dem Auffinden von systematischen Verfahren, die für ein gegebenes Problem eine korrekte Lösung sicherstellen. Solche Verfahren heißen Algorithmen.In der Mathematik kann man häufig Sätze in Formeln fassen. Das ist die einfachste Form einer Rechenvorschrift. Zum Beispiel: Die Fläche des Kreises mit Radius r beträgt A = Pi*r2.
Oft gibt es aber Situationen, in denen das Rechenschema nicht so einfach beschrieben werden kann. Klassische Beispiele hierfür sind die Polynomdivision, das Lösen von Linearen Gleichungssystemen und der euklidische Algorithmus zur Berechnung des größten gemeinsamen Teilers.
Die Beschreibung von Algorithmen erfordert folgende Eigenschaften:
- Sie muss eindeutig sein.
- Sie muss endlich beschreibbar sein.
- Das Verfahren muss terminiert sein. (Das heißt: es muss irgendwann beendet werden.)
Beispiele für Algorithmen sind:
- Vorschrift zum Zähneputzen (unabhängig von Zahnbürste und Paste)
- Kochbuchrezepte (linear)
- Überfahren einer Kreuzung unter Beachtung der Verkehrsregeln
- Berechne Idealgewicht aus Körpergröße und Geschlecht
- Abwasch in eine Wohngemeinschaft (A beauftragt B, B beauftragt C, ..., Z beauftragt A)
- 1+1/2+1/4+1/8+1/16+... (ad infinitum) kann so kein Computer
berechnen. Man muss dafür erst einen Algorithmus entwickeln.
Beispiel 9.1 Die Berechnung von y = xn (n natürliche Zahl).
(Diese Funktion ist aus Effizienzgründen nicht als Standardfunktion in Pascal implementiert.)
Bekanntlich bedeutet xn = x·x·x· ... ·x (n mal). Wie wir bereits wissen, berechnet man diese Produkt nach folgender Vorschrift.
| y := 1 (Anfangswert) |
| Multipliziere n mal y mit x |
function hoch(x:real; n:integer):real; var k:integer; begin result := 1; for k := 1 to n do result := x*result; end;Wenn man jedoch sehr oft Potenzen oder sehr hohe Potenzen (wie bei Verschlüsselungen) berechnen muss, ist diese Funktion nicht sehr effizient. Potenzen kann man auch mit sehr viel weniger Multiplikationen durchführen.
Beispiel y = 221
Rechne a:=2*2
b:=a*a (=24)
c:=b*b (=28)
d:=b*b (=216)
y:=d*b*2*1 (=216*24*2=221)
("*1" steht hier nur wegen des Anfangswertes beim Algorithmus.)
Statt 21 Multiplikationen hat man hier nur 7. Man sagt: Die Effizienz
dieser Methode ist besser. Diese Methode kann man folgendermaßen als Algorithmus formulieren:
| Anfangswert y:=1 |
| Wiederhole den folgenden Befehl solange, bis e=0 ist: Wenn e ungerade, dann y:=y·m und e:=e-1 (m ungeändert), sonst m:=2*m und e:=e/2 (y ungeändert) |
- Verfolgen wir den Algorithmus an unserem Beispiel y = 221 (m=2 e=21)
- y=1 m=2 e=21 (e gibt an, wie oft noch y mit m zu multiplizieren ist)
- y=2 m=2 e=20
- y=2 m=22 e=10
- y=2 m=(22)2=24 e=5
- y=2·24=25 m=24 e=4
- y=25 m=(24)2=28 e=2
- y=25 m=(28)2=216 e=1
- y=25·216=221 e=0
- fertig!
function hoch(m:extended; e:integer):extended;
begin
result := 1;
while e > 0 do
if odd(e) then Begin //odd(e) = true, wenn e ungerade
result := result*m;
e := e -1;
End else Begin
m :=m*m;
e := e div 2
End;
end;
Beispiel 9.2 Der Euklidische Algorithmus zur Berechnung des ggT.
Der ggT(a,b) ist der größte gemeinsame Teiler der Zahlen a und b.
zum Beispiel: ggT(18,12) = 6
ggT(5406,1785) = 51
Wenn du das zweite Beispiel nachprüfen willst, musst du dich schon ganz
schön anstrengen (Stichwort: Primfaktorenzerlegung). Bei sehr großen
Zahlen ist es so aussichtslos. Siehe Zur Primfaktorenzerlegung Mit Hilfe des euklidischen Algorithmus ist es jedoch kein Problem.
Jetzt machen wir uns die Tatsache zunutze, dass ein gemeinsamer Teiler von a und b auch Teiler von a - b ist.
Ist nämlich t ein gemeinsamer Teiler von a und b mit
a div t = x und
b div t = y (x, y ganze Zahlen), dann ist bekanntlich
———————————————————
(a - b) div t = x - y (Vertausche a und b, falls a < b).
Zum Beispiel:
143 div 13 = 11
52 div 13 = 4
———————————————————
91 div 13 = 7
Also:
ggT(a,b) = ggT(b,a - b)
Zum Beispiel:
ggT(143,52) = ggT(91,52), nämlich 13
Man kann sogar statt a - b auch
a - 2b oder
a - 3b ... nehmen.
Am besten ist natürlich
a - k·b für das größte k so, dass noch a -k·b > 0.
Es ist a mod b = a - k·b = Rest bei Division von a durch b
Also gilt auch hier: ggT(a,b) = ggT(b,a mod b)
Zum Beispiel: ggT(143,52) = ggT(52,143 - 2·52)
= ggT(52,39)
Beachte: 143/52 = 2 Rest 39
weiteres Beispiel: ggT(5406,1785) = ggT(1785, 5406 - 3·1785)
= ggT(1785, 51)
Beachte: 5406/1785 = 3 Rest 51
Jetzt können wir das Spiel wiederholen, bis der Rest Null ist.
ggT(1785,51) = ggT(51, 1785 - 35·51)
= ggT(51, 0)
Wir sehen: ggT(1785,51) = 51. Also ebenfalls ggT(5406,1785) = 51
Hier noch ein längeres Beispiel:
ggT(416,256) = ggT(256,160)
= ggT(160,96)
= ggT(96,64)
= ggT(64,32)
= ggT(32,0)
= 32
Der Algorithmus lautet:
| Wiederhole: |
|
solange durch b und (a mod b) |
| bis a mod b = 0. |
| Der ggT ist dann die letzte Zahl <> 0. |
Aufgabe 9.1: Schreibe ein Programm, das nach Eingabe eines Bruches den gekürzten Bruch ausgibt. Verwende dazu:
a a div ggT(a,b)
- = ——————————————
b b div ggT(a,b)
Das Formular könnte folgendermaßen aussehen:
Bruch(Label1) gekürzter Bruch(Label2)
spinedit1 spinedit3
————————— = —————————
spinedit2 spinedit4
Lösung
Aufgabe 9.2: Was gibt folgendes Programm aus?
function RoemischeMultiplikation(a,b: integer):integer;
var s: integer;
begin
form1.memo1.lines.Clear; //Nur zum Testen
s := 0;
repeat
form1.memo1.Lines.Add('a=' + IntToStr(a)
+ ' b=' + inttostr(b) + ' s=' + inttostr(s));//Test
if a mod 2 = 1 then s := s + b;
a := a div 2;
b := b*2;
until a = 0;
result:=s;
end;
procedure TForm1.Button1Click(Sender: TObject);
var x, y: integer;
begin
x:= 45;
y := 17;
memo1.lines.add('Erg.=' + IntTostr(RoemischeMultiplikation(x,y)));
//Bemerkung 45*17=(32 + 8 + 4 + 1)*17
end;
Lösung
Aufgabe 9.3: Ein Algorithmus zur Berechnung des Zweierlogarithmus a = lb(x) wird im Folgenden erklärt:
Der Näherungswert a für lb(x) wird laufend verbessert.
Setzte Anfangswert a=0 und y = x.
0
2 2 1
Ist y > 2, dann setze y = y - 2 und addiere - zu a,
0 1 0 2
2
andernfalls setze y = y und addiere nichts zu a.
1 0
2 2 1
Ist y > 2, dann setze y = y - 2 und addiere - zu a,
1 2 1 4
2
andernfalls setze y = y und addiere nichst zu a.
2 1
1 1 1
Fahre so fort und addiere gegebenenfalls -, ——, ——, ...
8 16 32
Schreib dazu eine passende Delphifunktion.Lösung: Programm zur Berchnung von lb(x)
10. Lektion: Rekursive Funktionen. I. Teil
Bei der Rekursion wird ein großes Problem in Teilprobleme zerlegt, die ähnlich strukturiert sind. Hier betrachten wir nur einen kleinen Ausschnitt von diesem Thema: Funktionen, die sich selbst aufrufen.
Man erhält damit häufig erstaunlich kurze, leicht verständliche und effiziente Algorithmen.
Beispiel 10.1:(iterativ siehe Beispiel 6.2)Das berühmteste Beispiel ist die Fakultät f(n)= n! =1·2·3·...·nBeispiel 10.2: Die Funktion kann auch mehrfach aufgerufen werden.1 falls n = 0 f(n) := { n*f(n-1) falls n > 0
Als Delphifunktion: function f(n: integer): real; begin if n < 1 then result := 1 else result := n*f(n-1) end; Wird zum Beispiel f(5) aufgerufen, muss man den Werten "hinterher rennen": f(5) = 5*f(4) mit f(4) = 4*f(3) mit f(3) = 3*f(2) mit f(2) = 2*f(1) mit f(1) = 1*f(0) mit f(0) = 1 (Anfangswert) Also f(5) = 5*4*3*2*1*1 Wichtig: Bei rekursiven Funktionen muss gewährleistet sein. I Das Problem wird auf einfachere Probleme reduziert. (Bei der Fakultät: Rechnung für ein kleineres n) II Nach endlich vielen Schritten ist das Problem ohne Rekursion lösbar. (Bei der Fakultät: Schließlich kommt man zu n = 0) Aufgabe 10.1: Schreibe ein Programm, das eine Wertetafel für f ausgibt. Aufgabe 10.2: Was wird bei der folgenden Funktion g berechnet? a) g(5) b) g(-5) function g(n: integer): real; begin if n = 0 then result := 1 else result := n*g(n-1) end; Aufgabe 10.3: Was wird bei folgender Funktion h berechnet? Gib nicht den Wert der Rechnung, sondern einen Rechenausdruck an! a) h(1.5,5) b) h(1.5,-5) c) Allgemein function h(x:real; n: integer): real; begin if n < 0 then result := 1/h(x,-n) else if n = 0 then result := 1 else result := x*h(x,n-1) end; Aufgabe 10.4: Was wird bei folgender Funktion berechnet? Gib nicht den Wert der Rechnung, sondern einen Rechenausdruck an! a) f(2) b) f(10) c) Allgemein function f(n: integer): real; begin if n < 0 then result := 0 else result := 1/(2*n+1) + f(n-1) end; Lösung
Ein berühmtes Beispiel dafür ist die Fibonacci-Folge.
|
Leonardo Fibonacci, eigentlich Leonardo von Pisa, 1170 - 1250, gehörte zum Gelehrtenkreis
Kaiser Friedrich II, führte die arabischen Ziffern in Europa ein. Er stellte in seinem Buch "Liber Abaci" folgende Aufgabe: |
| Ein Mann hält ein Kaninchenpaar an einem Ort, der gänzlich von einer Mauer umgeben ist. Wir wollen nun wissen, wie viele Paare von ihnen in einem Jahr gezüchtet werden können, wenn die Natur es so eingerichtet hat, dass diese Kaninchen jeden Monat ein weiteres Paar zur Welt bringen und damit im zweiten Monat nach ihrer Geburt beginnen. |
|
Man kommt dann auf die Zahlenfolge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
Es handelt sich um eine rekursive Funktion f mit f(0)=0 f(1)=1 und f(n)=f(n-1)+f(n-2) für n≥2. In geschlossener Form kann die Funktion als Binet-Formel angegeben werden. Nach 12 Monaten sind es also f(12)=233 Paare, alse 466 Kaninchen. |
| Es gibt viele interessante Eigenschaftren dieser Folge. Zum Beispiel konvergiert die Folge der aufeinander folgenden Zahlen 1/1, 1/2, 2/3, 3/5, 5/8, 8/13 ... gegen die vom goldenen Schnitt her bekannte Zahl (sqrt(5)-1)/2. Mit TTMathe kannst Du Dir den passenden Kettenbruch berechnen lassen. |
Die Fibonacci-Folge lautet rekursiv definiert:
1 für n = 1 und n = 2
f(n) = {
f(n-1) + f(n-2) für n > 2
Als Delphifunktion:
function fib(n:integer):integer;
begin
if n < 2 then result := 1
else result := fib(n-1) + fib(n-2)
end;
|
Aufgabe 10.5: Teste diese Funktion in einem Programm.
Lösung
Aufgabe 10.6: Die iterative Funktion fib(k) (siehe unten) benötigt zur Berechnung vom Wert fib(k) etwa k Additionen.
Schreibe ein Programm, das die Additionen bei der Verwendung der rekursiven Funktion von fib(k) zählt.
Lösung
Bemerkung1: Effizienter ist es, die Werte in einem Array zu speichern:
procedure TForm1.Button1Click(Sender: TObject);
const max = 500;
var n: integer;
nn: array[1..max] of real;
function f(n: integer): real;
//zuvor muss f(1), f(2), ..., f(n-1) aufgerufen sein
begin
if n <= 2 then result := 1
else result := nn[n-1] + nn[n-2];
nn[n] := result;
end;
begin
for n := 1 to max do
memo1.Lines.Add(inttostr(n) + ' ' +floattostr(f(n)));
end;
|
Bemerkung 2: Die Funktion fib "iterativ" geschrieben:
function fib(n:integer):integer;
var k, x1,x2: integer;
begin
result := 1; //für n=1 oder n=2
x1 := 1;
x2 := 1;
for k := 3 to n do Begin
result := x1 + x2;
x1 := x2;
x2 := result;
End;
end;
|
Nebenbei bemerkt: Es gibt sogar einen geschlossenen Ausdruck für die Funktion f(n)=fib(n):
Die Binet'sche Formel
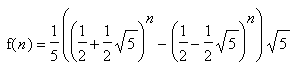 Kopierbar dargestellt:
Kopierbar dargestellt:
f(n) = 1/5*((1/2+1/2*sqrt(5))^n-(1/2-1/2*sqrt(5))^n)*sqrt(5)
wobei im Zähler die beiden Lösungen der Gleichung x2 - x - 1 = 0 vorkommen.
Herleitung der Binetschen Formel
Für geometrisch Interessierte: siehe Der goldene Schnitt oder die stetige Teilung
Aufgabe 10.7: Definiere die Funktion fib nach der Binet'schen Formel:
Hinweis: verwende result := round (...). Dann kann der Ergebnistyp der Funktion Integer sein.
Lösung
Beispiel 10.3 Potenzen effizient berechnen. (iterativ siehe hohe Potenzen.)
Die folgende Funktion zur Berechnung von me erklärt sich von selbst.
/ 1, falls e=0
|
|
e | e-1
m = | m·m , falls e ungerade
|
| e
| -
| 2 2
\ (m )
In Delphi:
function h(m:extended; e:integer):extended;
begin
if e = 0 then result := 1 else
if odd(e) then result := m*h(m,e-1)//da me=m*m(e-1)
else result := h(m*m,e div 2) //da me=(m*m)(e/2)
end;
Beispiel 10.4 Primfaktorenzerlegung
(iterativ Beispiel 7.10)
Die Rekursiosformel:
/ k*PFZ(n div k), falls k Teiler von m (k > 1 minimal}
PFZ(n) ={
\ n, sonst (d.h. n Primzahl)
wobei die Darstellung als String noch erforderlich ist.
In Delphi:
function PFZ(const n:integer):string;
var k:integer;
begin
for k:=2 to trunc(sqrt(n)) do
if n mod k = 0 then Begin
result:=intToStr(k)+'*'+PFZ(n div k); //rekursiv
exit;
End;
result:=intToStr(n);
end;
Beispiel 10.5 Der Euklidische Algorithmus (rekursiv):
function ggT(a,b:integer):integer; begin if b=0 then result := a else result := ggT(b, a mod b); //Rekursiv end;
|
Aufgabe 10.8: Was berechnet die Funktion f bei Eingabe von
a) n = 5 b) n = 10 c) n =-2 d) allgemein. Ergebnis bei allen Teilaufgaben als Rechenausdruck, falls möglich! |
function f(n: integer): real;
begin
if n <=0 then result := 0 else
result := 1/n + f(n-1);
end;
|
|
Aufgabe10.9: Was berechnet folgende Funktion bei Eingabe von a) n=3 b) n=5 c) n=10 d) n=-2 |
function f(n: integer): real;
begin
if (n=0) or (n=1) then result := 0 else
result := f(n-1) + 2*f(n-2);
end;
|
Lösungen
Beispiel 10.6 Die folgende Funktion berechnet "n über k".
n n·(n-1)·(n-2)·...(n-k+1) 49 49·48·47·46·45·44 ( ) = ——————————————————————— zum Beispiel ( ) =—————————————————— k 1 · 2 · 3 · ... ·k 6 1· 2· 3· 4 ·5 ·6
function nuebk(n,k: integer): integer; begin if k <= 0 then result := 1 else result := nuebk(n-1,k-1)*n div k; end;Diese Funktion wird bei der Binomialverteilung " benötigt.
Ein eigenes Kapitel, die Rekursion betreffend aber nun durchaus verständlich, ist die Programmierung eines mathematischen Parsers.
| zurück | Lösungen der Aufgaben | Inhalt |
|
