Homogene lineare rekursive Folgen 1. Grades ...

. . . sind von der Form a_n = p·a_n-1.

Ein geschlossener Ausdruck für a_n ist schnell gefunden und mit Hilfe der vollständigen Induktion bewiesen.

a_n = pⁿ·a₀

Lineare rekursive Folgen 1. Grades ...

. . . sind von der Form a_n = p·a_n-1 + c.
a₀ = a (Anfangswert)
a₁ = p·a + c
a₂ = p·(p·a + c) + c = p²·a + c·(p+1)
a₃ = p·(p²·a + c·(p+1)) + c = p³·a + c(p² + p + 1)
. . . (man ahnt schon wie es weitergeht)
a_n = pⁿ·a + c(1 + p + p² + ... + p^n-1)
Die geometrische Reihe kann durch einen geschlossenen Ausdruck dargestellt werden.

Somit ist

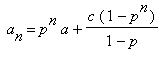
Kopierbar dargestellt:

a_n = p^n*a + c((1-p^n)/(1-p))       (p≠1)

Beweisen kann man die Formel leicht mit Hilfe der vollständigen Induktion.
(Für p=1 ist a_n = a + n·c).

Homogene lineare rekursive Folgen 2. Grades ...

. . . sind von der Form a_n = p·a_n-1 + q·a_n-2.

Man findet folgendermaßen für a_n einen geschlossenen Ausdruck:

Bestimme die beiden Lösungen x₁ und x₂der charakteristischen Gleichung


x² - p·x - q = 0


Dann ist a_n = c₁x₁ⁿ + c₂·x₂ⁿ ,

wobei sich die Koeffizienten c₁ und c₂ aus den Anfangsgleichungen

a₀ = c₁ + c₂ und

a₁ = c₁·x₁ + c₂·x₂

ergeben.

Beweis über die starke vollständige Induktion:

I. Induktionsanfang: ist nach Voraussetzung erfüllt. (Koeffizienten c₁ und c₂ werden ja gerade so bestimmt, dass die Formel für a₀ und a₁ erfüllt ist.)

II. Induktionsschritt. Sei für n > 1 gültig: a_n = c₁x₁ⁿ + c₂·x₂ⁿ und a_n-1 = c₁x₁^n-1 + c₂·x₂^n-2.

Zu zeigen ist: a_n+1 - c₁x₁ⁿ⁺¹ - c₂·x₂ⁿ⁺¹ = 0

Nachweis: a_n+1 - c₁x₁ⁿ⁺¹ - c₂·x₂ⁿ⁺¹
=p·a_n-1 + q·a_n-2 - c₁x₁ⁿ⁺¹ - c₂·x₂ⁿ⁺¹
=p·(c₁x₁^n-1 + c₂·x₂^n-1) +q·(c₁x₁^n-2 + c₂·x₂^n-2) - c₁x₁ⁿ⁺¹ - c₂·x₂ⁿ⁺¹
= -x₁^n-2·c₁·(x₁²-p·x₁-q) -x₂^n-2·c₂·(x₂²-p·x₂-q)
= -x₁^n-2·c₁·0 - x₂^n-2·c₂·0 = 0 ∎

a) Beispiel: Fibonaccizahlen

Die Fibonaccizahlen f(n) sind definiert durch

f(0) = 0
f(1) = 1
f(n)= f(n-1) + f(n-2) für n > 1

Die charakteristische Gleichung x₂ - x - 1 = 0 hat die Lösungen

           -                -
      1 + √5           1 - √5
x   = ——————  und x  = ——————
 1      2          2     2

Mit 0 = c + c    und 1 = c ·x  +  c ·x
         1   2            1  1     2  2

                 1  -            1  -
ergibt sich c =  -·√5  und c = - -·√5
             1   5          2    5

und somit die Die Binet'sche Formel

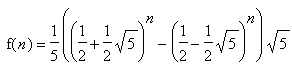
Kopierbar dargestellt:


f(n) = 1/5*((1/2+1/2*sqrt(5))^n-(1/2-1/2*sqrt(5))^n)*sqrt(5)

b) Zweites Beispiel

Die Folge sei definiert durch

a₀ = 1, a₁ = 0 und a_n = 1/2·(a_n-1 + a_n-2) für n > 1

Die charakteristische Gleichung 2x² - x - 1 = 0 hat die Lösungen

x₁ = 1 une x₂ = - 1/2.

Mit den Anfangswerten errechnit sich

     1   2    1 n
a  = - + -·(- -)  für n = 0,1,2 ...
 n   3   3    2

                               1  1  3   5  11  21   43                     1
Es ergibt sich die Folge 1, 0, -, -, -, ——, ——, ——, ———   mit dem Grenzwert -
                               2  4  8  16  32  64  128                     3