Joachim Mohr Mathematik Musik Delphi

Wahrscheinlichkeitstheorie

ein Crashkurs für Abiturienten

Tipp: Schreibe zunächst einmal auf, was gegeben und was gesucht ist. Zum Beispiel:
n=? p=0,51 P(X≥5)≥0.99. (Die zugehörige Aufgabe sieht erbarmungslos kompliziert aus.)
Egal um was es geht, die Lösung erhält man mit Hilfe der Tabelle. Gesucht: P(X≤4)<0.01

n=10 P(X≤4)= 0,352 Hinweis: GTR P(X≤4)=binomcdf(10,0.51,4)
                   Die "binomial cumulatated distribution function"
...
n=18 P(X≤4)= 0,012  noch zu groß
n=19 P(X≤4)= 0,008  Ergebnis: n=19

Vorübung: 50%=½ und 100%=1

3   3     3                 1   100
- = -·1 = -·100% = 75%      - = ———% = 16,7% u.s.w.
4   4     4                 6    6

0,13 = 13%      0,0458 = 4,58% u.s.w.

          1     75   3            27
75% = 75·——— = ——— = -     27% = ———  u.s.w.
         100   100   4           100

Zufallsexperimente

Beispiel eines Zufallsexperimente: Werfen eines idealen Würfels.
Beispiel für ein Elementarereignis: "Es fällt eine 6". In Mengenschreibweise E={6}
Beispiel für ein Ereignis: "Es fällt eine gerade Augenzahl". In Mengenschreibweise A={2;4;6}
Die Ergebnismenge ist M = {1;2;3;4;5;6}

Bei einem idealen Würfel ist die Wahrscheinlichkeit jedes Elementarereignisses gleich:
P({1})=P({2})=P({3})=P({4})=P({5})=P({6})=¹/₆= 16,7%.

P({2;4;6}) = P({2}) + P({4}) +P({6}) = ³/₆ = 50%.

Mehrstufiges Zufallsexperimente: Werfen von zwei idealen Würfeln.(Der Ausgang der Würfe ist unabhängig von einander.)
Die Wahrscheinlichkeit einer Doppelsechs berechnet sich als Produkt:
"1. Wurf eine 6, dann 2. Wurf eine 6":
P{(6 6)} = ¹/₆·¹/₆=2,8%
Die Wahrscheinlichkeit "keine Doppelsechs" (Gegenereignis) = 1 - P{(6 6)} = ³⁵/₃₆=97,2%.

Chevalier de Mére, ein leidenschaftlicher Spieler, stellte 1654 Blaise Pascal folgende Frage: Ist die Wahrscheinlichkeit für mindestens eine Doppelsechs beim 24-maligen Werfen zweier Würfel größer oder kleiner als 50%?

Lösung: Betrachte das Zufallsexperimentes mit unendlich vielen Ausgängen:
Zwei Würfel werden solange geworfen, bis eine Doppelsechs erscheint. Im folgenden "1" für Doppelsechs und "0" sonst.
Die Ergebnismenge ist M={(1) (0 1) (0 0 1) (0 0 0 1) (0 0 0 0 1) ...}
Die Wahrscheinlichkeiten der Elementarereignisse sind:

                     1
    p({(1)}       = ——
                    36

                    35  1
    p({(0 1)}     = ——·——
                    36 36

                    35 35  1
    p({(0 0 1)}   = ——·——·——
                    36 36 36

    ...

Addieren wir die Wahrscheinlichkeiten der Anfangsergebnisse, erhalten wir die Antwort auf die Frage.


M={   (1)  (0 1) (0 0 1) (0 0 0 1) (0 0 0 0 1) ...             }

Würfe  1     2      3       4          5       ...   24     25

p     2,78% 2,70% 2,63%  2,55%      2,48%      ...  1,45%  1,41%

Summe 2,78% 5,48% 8,10% 10,66%     13,14%      ... 49,14% 50,55%

Chevalier de Mére forderte seinen Gegner auf, 24 mal zu würfeln. Tritt dabei eine Doppelsechs auf, bekommt der Gegner 100 Louis d'or, im anderen Fall der Herausforderer. Er hat öfters gewonnen als sein Gegner. Das war kein Zufall sondern Berechnung! 1654 gilt als das Geburtsjahr der Wahrscheinlichkeitstheorie,

Urnenmodell

In einer Urne befinden sich 6 Kugeln durchnummeriert. Es werden zwei Kugeln gezogen. Wie groß ist die Wahrscheinlichkeit für das Ergebnis "die 5 und die 6 wurden gezogen"?

Mit Zurücklegen

Das ist das Modell für zweimaliges Werfen eines Würfels oder des Werfens von zwei Würfeln.
P{(5 6)} + P{6 5} = 1/6·1/6 + 1/6·1/6 = 5,6%

Ohne Zurücklegen

In diesem Fall ist der Ausgang der zweiten Ziehung abhängig von der ersten (Wenn die erste Kugel gezogen ist gibt es für die zweite nur noch 5 Möglichkeiten).
P{(5 6)} + P{6 5} = 1/6·1/5 + 1/6·1/5 = 1/15 = 6,7%

Mit einem Griff

Mit einem Griff zwei Kugeln aus 6 zu ziehen berechnet sich nach der Formel:

 6    6·5
( ) = ——— = 15. Die Wahrscheinlichkeit für ein solches Ereignis
 2    1·2

           1
ist dann  —— = 6,7%
          15




                    n
n! (Fakultät) und  ( ) (n über k)
                    k



                            49
0!=1                       (  ) = 1
                             0
1!=1
                            49    49
2!=1·2=2                   (  ) = —— = 49
                             1     1
3!=1·2·3=6
                            49    49·48
4!=1·2·3·4=24              (  ) = —————
                             2     1·2
5!=1·2·3·4·5=120
                              ...
...
         "6 aus 49"        49    49·48·47·46·45·44
                          (  ) = ————————————————— = 13 983 816
      "mit einem Griff"     6     1· 2· 3· 4· 5 ·6

Nebenbei bemerkt: An dieser Erklärung kann man sehr gut den Begriff "Rekursive Definition" einführen:
(Für Programmierer eine wunderbare Sache: Man erhält damit häufig erstaunlich kurze, leicht verständliche und effiziente Algorithmen. )

       1, falls n = 0
n! =  {                        Definition für n≥0
       n·(n-1)! für n > 0

Danach berechnet sich zum Beispiel

3! = 3·2!

   = 3·2·1!

   = 3·2·1·0!

   = 3·2·1·1

          n     /  1, falls k=0
Anaolog: ( ) = {                    Definition für k≥0, nεZ
          k     \  n  n-1
                 \ -·(   )  für k > 0
                  \k  k-1

Danach berechnet sich zum Beispiel

 49    49  48    49 48  47          49 48 47 46 45 44
(  ) = ——·(  ) = ——·——·(  ) = ... = ——·——·——·——·——·——·1
  6     6   5     6  5   4           6  5  4  3  2  1

Binomialverteilung

Beispiel einer symmetrischen Binomialverteilung: Werfen von 6 idealen Münzen
(Bernoulli-Kette: n=6 p=1/2 q=1-p=1/2). Die Ergebnismenge ist
M={(0 0 0 0 0 0); (0 0 0 0 0 1); ... ;(1 1 1 1 1 0); (1 1 1 1 1 1)}. M enthält 64 Ereignisse, alle mit der Wahrscheinlichkeit von ¹/₆₄.
(0 entspricht Wappen, 1 entspricht Zahl).
Jedes Elementarereignis hat die Wahrscheinlichkeit 1/2·1/2·1/2·1/2·1/2·1/2=1/64 (Berechnung nach der Pfadregel).
Eine große Vereinfachung bringt die Schreibweise mit einer Zufallsvariable X:
Zum Beispiel sei die Zufallsvariable X definiert als "Anzahl der Treffer":
Schreibweise (X=0) bedeutet Ereignis A = {(0 0 0 0 0 0)} (A enthält ein Elemente)
Schreibweise (X=1) bedeutet Ereignis B = {(0 0 0 0 0 1) (0 0 0 0 1 0) (0 0 0 1 0 0) (0 0 1 0 0 0) (0 1 0 0 0 0) (1 0 0 0 0 0)} (B enthält 6 Elemente)
Schreibweise (X=2) bedeutet Ereignis C = {(0 0 0 0 1 1) (0 0 0 1 0 1) ... (1 1 0 0 0 0)} (C enthält 15 Elemente)
u.s.w.

Die Wahrscheinlichkeiten dieser Ereignisses berechnet sich durch Abzählen der Elementarereignisse.

                            6  1     1
P(X=0)=P({(0 0 0 0 0 0)} = ( )·—— = —— = 1,6%
                            0  64   64

P(X=1)=P({0 0 0 0 0 1);

         (0 0 0 0 1 0);

         (0 0 0 1 0 0);

         (0 0 1 0 0 0);

         (0 1 0 0 0 0);
                           6   1      1
         (1 0 0 0 0 0)} = ( )·—— = 6·—— = 9%
                           1  64     64

P(X=2) = P({0 0 0 0 1 1);

           {0 0 0 1 0 1);

           {0 0 0 1 1 0);

           {0 0 1 0 0 1);

           {0 0 1 0 1 0);

           {0 0 1 1 0 0);

           {0 1 0 0 0 1);

           {0 1 0 0 1 0);

           {0 1 0 1 0 0);

           {0 1 1 0 0 0);

           {1 0 0 0 0 1);

           {1 0 0 0 1 0);

           {1 0 0 1 0 0);

           {1 0 1 0 0 0);
                             6   1        1
           {1 1 0 0 0 );) = ( )·——  = 15·—— = 23%
                             2  64       64

Entsprechend berechnet sich

          6   1       1
P(X=3) = ( )·—— = 20·—— = 31%
          3  64      64

          6   1       1
P(X=4) = ( )·—— = 15·—— = 23%
          4  64      64

          6   1      1
P(x=5) = ( )·—— = 6·—— = 9%
          5  64     64

          6   1    1
P(X=6) = ( )·—— = —— = 1,6%
          6  64   64

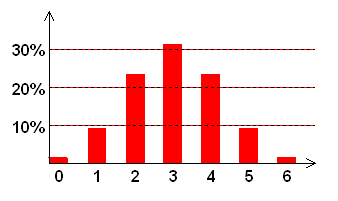
Alles zusammen: P(X=0) + P(x=1) + ... P(X=6) = 1 = 100%.

Die Simulation eine Binomialverteilung am Galtonbrett

Download

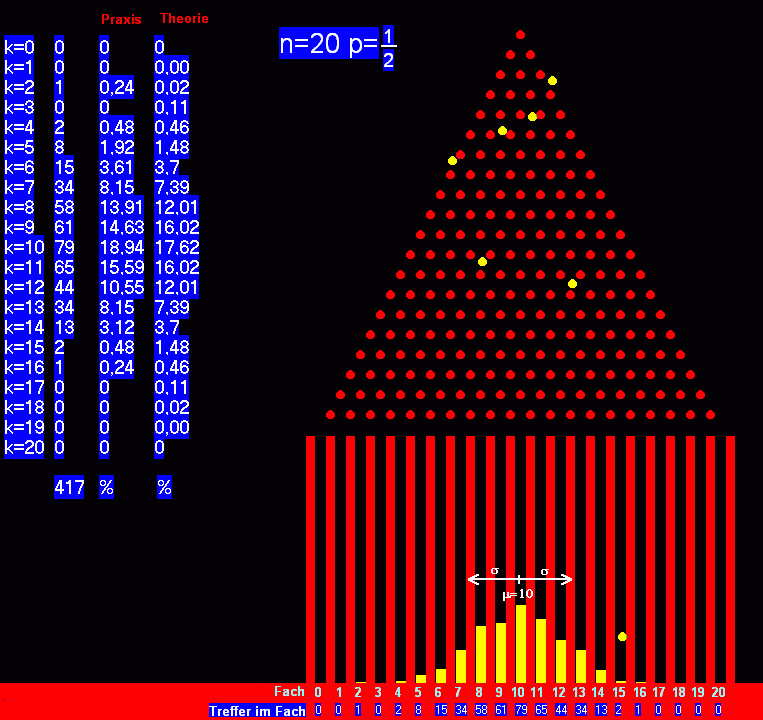
Beim Galton-Nagelbrett rollen Kugeln herab und werden an jedem Nagel nach links oder rechts abgelenkt.
Dies ergibt eine Binomialverteilung.

                    1             20   1 12  1 8
Hier ist n=20 und p=- => P(X=12)=(  )·(-)  ·(-) = 12% (zum Beispiel).
                    2             12   2     2

Die herab gerollten Kugeln sammeln sich in den Fächern "Fach X=0" bis "Fach X=20" Im Beispiel sind 417 Kugeln gefallen. Im "Fach X=12" sind 44 Kugeln eingetroffen, theoretisch 12% von 417 Kugeln also 50 Kugeln.

Der Mittelwert und die Standardabweichungen errechnen sich zu m=10 und s=2,24.

Hier ist theoretisch P(m-s≤X≤m+s) =P(7,76≤X≤12,76)=P({8 9 10 11 12})=0,120+0,160+0,176+0,160+0,120=74%. Das entspräche 307 Kugeln bei einer Gesamtzahl von 417

Kugeln. In unserem Versuch liegen in der Fächern X=8 bis X=12 tatsächlich 307 Kugeln.

Beispiel einer unsymmetrischen Binomialverteilung:
Werfen von 6 idealen Würfeln (Treffer: die 6 fällt, sonst Niete).
Gezählt wird, wie oft die 6 fällt. (Bernoulli-Kette:n=6 p=1/6 q=1-p=5/6).
Die Ergebnismenge ist (0 entspricht: keine 6, 1 entspricht die 6 ist gefallen):
M={(0 0 0 0 0 0); (0 0 0 0 0 1); ... ;(1 1 1 1 1 0); (1 1 1 1 1 1)}.
Wird ein Würfel geworfen, so ist die Wahrscheinlichkeit "für eine 6" p=1/6, die Wahrscheinlichkeit "für keine 6" q=5/6.

Die Zufallsvariable X hier zählt, wie oft eine 6 gefallen ist.

          6   6
P(X=0) = ( )·q     = 33%
          0

          6   5
P(X=1) = ( )·q·p   = 40%
          1

          6   4  2
P(X=2) = ( )·q ·p  = 20%
          2

          6   3  3
P(x=3) = ( )·q ·p  = 5%
          3

          6   2  4
P(X=4) = ( )·q ·p  = 0,8%
          4

          6     5
P(x=5) = ( )·q·p   = 0,06%
          5

          6   6
P(X=6) = ( )·p    = 0,002%
          6

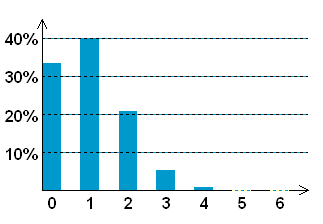
Zusammen: 100%

Aufgaben:

1. Aufgabe (gesucht P(X=k) etc.): Es wird 100 mal gewürfelt (Treffer: "die 6 fällt"). Wie groß ist die Wahrscheinlichkeit, dass
a) genau 17 Treffer (17 mal die 6 fällt?.
b) höchsten 17 Treffer dabei sind?
c) mindestens 18 Treffer dabei sind?
d) Zusatz: Berechne Mittewert m und Standardabweichung s, sowie P(m-s≤X ≤m+s).
Lösung: Es handelt sich um eine Binomialverteilung, da die einzelnen Würfe unabhängig voneinander sind. Dabei ist n=100, p=1/6 und q=5/6.
a) P(X=17) = 11 % [GTR: binompdf(100,1/6,17)].

                   100   17  83
Formel: P(X=17) = (   )·p  ·q   = 0,1052 = 10,52%
                    17

b)P(X≤17) = 60%.

                                  100   100     100   17  83
Formel: P(x=0) + ... + P(X=17) = (   )·p + ... (   )·p  ·q   = 60%
                                   0             17

c) P(X≥18) = 1 - P(X≤17) = 100% - 60% =40%

Solch eine Aufgabe wird mit Hilfe des Gegenereignisses berechnet.

                    —————————
d) m=n·p=16,67; s=\/n·p·(1-p)=3,73

P(13≤X≤21) = P(X≤21)-P(X≤12) = 0,8998 - 0,1297 = 77%



  Berechnung beim GTR mit Binomial Probability Distribution Funktion

   n   k  n-k
  ( )·p ·q    = binompdf(n,p,k)
   k

    Binomial Cumulated Distribution Funktion
   n  k          n   k  n-k
  ( )p  + ... + ( )·p ·q     = binomcdf(n,p,k)
   0             k

2. Aufgabe (Gesucht n): 15% der Ärzte (eingeschlossen auch Ärztinnen) sind Raucher. Bei einem Ärztekongress befinden sich in der Pause 5 Raucher vor dem Haus. Wie groß muss die Kongressteilnehmerzahl mindestens sein, damit mit einer Wahrscheinlichkeit von 90% so viel rauchen.

Bemerkung: Mit gesunden Menschenverstand würde man argumentieren. 15 von 100 sind Raucher, bei 33 Teilnehmern sind es 5. Also sind - grob geschätzt - 33 Ärzte beim Kongress. Aber diese Schätzung ist doch ziemlich unsicher? Es könnten auch 100 Ärzte bei dem Kongress sein und - zufällig - eben nur 5 Raucher dabei.

Lösung:

Bei diesem Aufgabentyp geht die Lösung stets über die Binomialverteilung (Begründung dafür ist die Unabhängigkeit der Einzelereignisse. Dies stimmt zwar nicht exakt, aber es stimmt um so besser, je größer die Menge ist, aus der die Stichprobe entnommen wird.). Wenn man jetzt noch herausbekommt, was gegeben und gesucht ist, hat man schon einen wesentlichen Teil der Lösung erreicht. Und das ist gar nicht so schwierig. Jetzt muss man auch noch darauf gefasst sein, dass die Lösung nicht errechnet werden kann, sondern mit Hilfe von Tabellen oder durch Probieren gefunden werden muss.

Bekannt p=0,15, P(X≥5)≥0,9 bzw. P(X≤4)≤0,1. Gesucht n.
Geht man davon aus, dass Raucher zu sein, unabhängig von einander ist, handelt es sich um eine Binomialverteilung mit p=0,15 und q=0,85. X sei die Zufallsvariable, die die Raucher zählt. Mit P(X≥5) = 1 -P(X≤4) berechnen wir P(X≤4) mit ansteigendem n solange, bis P(X≤4) ≤ 10%.

  


          n      n     n       n-1        n      n-2     2
P(X≤4) = ( )·0,15   + ( )·0,15   ·0,85 + ( )·0,15   ·0,85
          0            1                  2

      n      n-3     3    n      n-4     4
   + ( )·0,15   ·0,85  + ( )·0,15   ·0.85 = binomcdf(n,0.15,4)
      3                   4

Herantasten:

n=50 P(X≤4) = 11,2% noch zu groß

n=51 P(X≤4) = 10,2% noch zu groß

n=52 P(X≤4) = 9,3%

Ergebnis: Bei mindestens 52 Teilnehmern sind 5 Raucher dabei. Man kann dies mit einer Sicherheit von 90% behaupten.

3. Aufgabe:: Eine Zulieferfirma einer Autofabrik vereinbart, dass ihre Bauteile abgenommen werden, wenn höchstens zwei einer Stichprobe von 100 sich als fehlerhaft erweisen. Die Zulieferfirma möchte dies mit eine Zuverlässigkeit von 98% erreichen. Genügt es, wenn bei der Zulieferfirma intern das Qualitätsniveau bei 1% angesetzt werden?
Lösung:

Bei diesem Aufgabentyp geht die Lösung stets über die Binomialverteilung. Wenn man jetzt noch herausbekommt, was gegeben und gesucht ist, hat man schon die halbe Lösung. Und das ist gar nicht so schwierig.
Bekannt: n=100, p=1% (dies muss eventuell auch erraten werden) und P(X≤2)=0,98.

Das interne Ausfallrisiko eines Bauteiles sei p. Die Zufallsvariable X zähle die defekten Bauteile für n=100.

Für p=1%=0,01 erhält man

          100  100    100  99         100  98
P(X≤2) = (   )p    + (   )p  (1-p) + (   )p  ·(1-p) = 92,1 %
           0           1               2

Ergebnis: 1% genügt nicht für das interene Qualitätskriterium.

Um das richtige p zu ermitteln, wird eine Wertetafel für p benötigt oder evetuell der Schnittpunkt des Schaubildes mit der Geraden y=0,98 näherungsweise ermittelt.

Für p=0,9% ist P(X≤2)=93,8%,
Für p=0,8% ist P(X≤2)=95,3%,
Für p=0,7% ist P(X≤2)=96,6%,
Für p=0,6% ist P(X≤2)=97,7% und
Für p=0,5% ist P(X≤2)=98,6%

Ergebnis: Das interne Qualitätsniveau muss ¹/₂% betragen, d.h. durchschnittlich darf nur bei 200 Stück höchstens ein fehlerhaftes sein.

Ergebnis: Die Firma muss bestrebt sein, dass interne Fehlerrisiko auf 1% zu drücken.

Erwartungswert und Standardabweichung bei Binomialverteilungen

Diese spielen nur bei großem n eine Rolle.

Erwartungswert ist m=n·p
                          —————
Standardabweichung ist s=√n·p·q mit q = 1-p.

Bei großem n gilt:

P = P(m-s≤X≤m+s)    ≈ 68,3%,
 1
P = P(m-2s≤X≤m+2s)  ≈ 95,4% und
 2
P = P(m-3s≤X≤m+3s)  ≈ 99,7%.
 3

1.Beispiel

        1   1
n=100 p=- q=- m=50 s=5
        2   2

P = P(45≤X≤55) = 68%
 1

P = P(40≤X≤60) = 95%
 2

P = P(35≤X≤65) = 99,7%
 3

2.Beispiel

        1   3
n=100 p=- q=-  m=25 s=4,33
        4   4

P = P(21≤X≤29) = 63,9%
 1

P = P(17≤X≤33) = 96,4%
 2

P = P(12≤X≤37) = 99,6%
 3

3.Beispiel

        1   7
n=100 p=- q=-  m=12,5 s=3,31
        8   8

P = P(10≤X≤15) = 53,9%
 1

P = P(6≤X≤19) = 95,1%
 2

P = P(3≤X≤22) = 99,6%
 3

4.Beispiel

         1   7
n=1000 p=- q=-  m=125 s=10,46
         8   8

P = P(115≤X≤135) = 66,0%
 1

P = P(105≤X≤145) = 94,4%
 2

P = P(94≤X≤156) = 99,7%
 3

5.Beispiel (n klein)

       1   1
n=20 p=- q=-  m=10 s=2,24
       2   2

P = P(8≤X≤12) = 61,7%
 1

P = P(6≤X≤14) = 92,1%
 2

P = P(4≤X≤16) = 99,2%
 3

5.Beispiel (n klein, p <<0.5 )

       1     9
n=20 p=—— q=——  m=2 s=1,34
       10   10

P = P(1≤X≤3) = 47,5%
 1

P = P(0≤X≤4) = 83,5%
 2

P = P(0≤X≤6) = 87,6%
 3

Statistik

Statistik ist ein Verfahren,
welches es gestattet,
geschätzte Größen
mit der Genauigkeit von
Hundertstelprozent
auszudrücken.
Helmar Nahr (Mathematiker, * 1931)

Schwindel, Lüge, Statistik ...
Folklore

Während die Wahrscheinlichkeitsrechnung die mathematische Theorie von Unsicherheiten beschreibt (wie oft man zum Beispiel im Durchschnitt eine Doppelsechs wirft), werden in der Statistik mathematische Modelle beschrieben, nach denen dann Entscheidungen angesichts von Unsicherheiten getroffen werden (ob zum Beispiel ein neues Medikament besser als ein bisher verwendetes ist.)

Es geht darum, Aussagen für eine ganze Population mit Hilfe einer Stichprobe zu machen. Solch ein Verfahren ist jedoch voller Gefahren, wenn man den gesunden Menschenverstand ausschaltet.

Der zweiseitige Signifikanztest

Gegeben: p (genannt die Nullhypothese H₀), der Stichprobenumfang n und das Signifikanzniveau a=5% (zum Beispiel).
Gesucht: Der Annahmebereich [a;b] mit P(a≤X≤b)≥95%.
Eine Vereinfachung erhält man durch die s-Regel, die besagt dass P(m - 2s ≤ X ≤ m + 2s) ≥95%.
Idee dahinter: Man möchte die Nullhypothese nur verwerfen, wenn die Irrtumswahrscheinlichkeit dafür gering ist. Je kleiner a gewählt wird, um so schwieriger ist es, die Nullhypothese zu verwerfen.

1. Beispiel: p=0,15; n=1000; a=5%.
Mittelwert m=150 Standardabweichung s=11,29.
Daraus folgt: Der Annahmebereich ist [m-2s;m+2s] gerundet auf ganze Zahlen [128;172]. Liegt die Trefferzahl der Stichprobe in diesem Bereich, wird die Nullhypothese H₀ p=0,15 angenommen, im anderen Fall verworfen.

2. Beispiel: p=0,15; n=1000; a=1%.
Hier müssen die Werte von a und b mit Hilfe einer Tabelle ermittelt werden.
P(a≤X≤b)≥99% heißt: P(Xb)<0,5%. Oder: P(X0,5% und P(X≤b)>99,5%.
In einer Tabelle kann man ablesen:

P(X=120)=0,003689695 zu klein  |  P(X=175)=0,986765272 zu klein
                               |
...                            |  ...
                               |
P(X=121)=0,004865258 zu klein  |  P(X=179)=0,994729593 zu klein
                               |
P(X=122)=0,006359935 passt!    |  P(180)=0,995876937 passt!

Ergebnis: Liegt die Trefferzahl der Stichprobe im Bereich [122;180], so wird die Nullhypothese H₀ p=0,15 angenommen, im anderen Fall verworfen.

Die Behauptung p=0,15 (eines Zulieferers) zurückzuweisen, ist also im 2. Beispiel schwieriger als im 1. Beispiel.

Der linksseitige einseitige Signifikanztest

Standardbeispiel: Bei einem Würfelspiel wird behauptet: Der Würfel liefert zu wenig Sechsen.
Nullhypothese: H₀: p=¹/₆. Die Alternative wäre p<¹/₆.
H₀ wird abgelehnt, wenn mit einer Wahrscheinlichkeit von zum Beispiel 5% bei n=300 Würfen höchsten 39 Sechsen fallen (Berechnung an Hand einer Tabelle: siehe unten). Was heißt das?

Bei der Hypothes H₀ zu wäre bei n=300 zu erwarten: ³⁰⁰/₆ = 50 Sechsen.
Um die Behauptung zu stützen, der Würfel liefere zu wenig Sechsen, müßten also "wesentlich" weniger Sechsen fallen.
Der Zufall spielt aber hier eine große Rolle. Es können bei der Nullhypothese "zufällig" auch "wesentlich" weniger Sechsen fallen. Dieser Zufall läßt sich berechnen.

Zum Beispiel: Die Wahrscheinlichkeit dass nur 39 Sechsen oder weniger fallen ist kleiner als 5%.

Wie wird der Ablehnungsbereich [0;39] für die Nullhypothese H₀ berechnet?
Antwort: Mit Hilfe einer Tabelle für n=300 und p=¹/₆.

  P(X=0) =0,000000000000000000000001760460139 zu klein
  P(X≤10)=0,0000000000003
  P(X≤20)=0,0000002
  P(X≤30)=0,00070
  P(X≤40)=0,068  =6,8%                        zu groß

  Verfeinerung:

  P(X≤35)=0,0099
  P(X≤36)=0,0154
  P(X≤37)=0,0232
  P(X≤38)=0,0340
  P(X≤39)=0,0485 = 4,85%                      noch passend
  P(X≤40)=0,068  = 6,8%                       zu groß

Aufgabe: Berechne den linksseitigen Ablehnungsbereich für die Nullhypothese H₀: p=70% bei n=100 und einem Signifikanzniveau von 5%.

Lösung mit Hilfe einer Tabelle für n=100 und p=0,7

...
P(X≤60) = 0,021
P(X≤61) = 0,033
P(X≤62) = 0,530 zu groß
...

Ergenis: Der Ablehnungsbereich ist [0;61].

Aufgabe: Das Gerät A wird mit einer Wahrscheinlichkeit von 2% innerhalb der Garantiezeit defekt. Ein neu entwickeltes Gerät B soll besser sein. Wie viele Geräte B dürfen bei einer Stichprobe von 500 Stück höchstens ausfallen, dass mit einem Signifikanzniveau von 5% behauptet werden kann, das Gerät B sei besser.

Lösung: n=500 H₀: p=0,02. Tabelle:

  P(X=0)=0,000041024
  P(X≤1)=0,000459636
  P(X≤2)=0,002591141
  P(X≤3)=0,009812156
  P(X≤4)=0,028122586 = 2,8%
  P(X≤5)=0,065191867 = 6,5%

Ergebnis: Es dürfen bei 500 Stück von Gerät B höchstens 4 ausfallen. Dann kann mit ziemlicher Sicherheit behauptet werden, es ist besser. (Beachte: 2% von 500 Geräten A sind 10 Stück. 4 von 500 Stück Gerat B sind 0,8%)

Der rechtsseitige einseitige Signifikanztest

Standardbeispiel: Bei einem Würfelspiel wird behauptet: Der Würfel liefert zu viel Sechsen.
Nullhypothese: H₀: p=¹/₆. Die Alternative wäre p>¹/₆.
H₀ wird abgelehnt, wenn mit einer Wahrscheinlichkeit von zum Beispiel 5% bei n=300 Würfen mindestens 62 Sechsen fallen. (Siehe Tabelle)

...
(PX≥60)=1-P(X≤59)=1-0,927006949=0,072993051
(PX≥61)=1-P(X≤60)=1-0,945359034=0,054640966=5,4%
(PX≥62)=1-P(X≤61)=1-0,959800019=0,040199981=4,0%
...

Aufgabe: Berechne den rechtsseitigen Ablehnungsbereich für die Nullhypothese H₀: p=70% bei n=100 und einem Signifikanzniveau von 5%.

Lösung mit Hilfe einer Tabelle für n=100 und p=0,7

...
P(X≥79) = 1 - P(X≤78) = 1 - 0,971 = 2,9%
P(X≥78) = 1 - P(X≤77) = 1 - 0,952 = 4,7%
P(X≥77) = 1 - P(X≤76) = 1 - 0,924 = 7,5% zu groß
...

Ergebnis: Der Ablehnungsbereich ist [78;100].

Aufgabe: Berechne den rechtsseitigen Ablehnungsbereich für die Nullhypothese H₀: p=70% bei n=1000 und einem Signifikanzniveau von 5%.

Lösung mit Hilfe einer Tabelle für n=1000 und p=0,7

...
P(X≥724) = 1 - P(X≤724) = 4,5%
P(X≥725) = 1 - P(X≤723) = 5,2% zu groß
...

Ergebnis: Der Ablehnungsbereich ist [724;1000].

Aufgabe:Ein bewährtes Medikament A bringt in 80% der Fälle eine Besserung. Ein neu entwickeltes Medikament B erhält den Vorzug, wenn es "signifikant" besser ist. Wann erhält es bei einem Test an 2000 Patienten bei einem Signifikanzniveau von 1% den Vorzug?

Lösung:n=2000 H₀: p=0,8 Tabelle:

(PX≥1600)=1-P(X≤1599)=51,3% noch viel zu klein! (1600 wären 80% von 2000)
...
(PX≥1640)=1-P(X≤1639)=1,3%
(PX≥1641)=1-P(X≤1640)=1,1%  noch zu groß
(PX≥1642)=1-P(X≤1641)=0,95% passt!
...

Ergebnis: Ab 1642 Heilungen erhält Medikament B den Vorzug.

Man kann hier erahnen: Je größer die Stichprobe, um so weniger muss die Verbesserung gegenüber dem Erwartungswert von H₀ sein. (Beachte: 1642 Heilungen bei 2000 sind 82%).