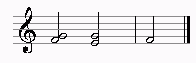Joachim Mohr Mathematik Musik
Hörbeispiele
Beim Gebrauch von Instrumenten mit 12 Tönen in der Oktave ist man genötigt, Kompromisse einzugehen. Welche Tonleitern sind spielbar?Rein gestimmt: Nur eine Tonleiter.
mitteltönig gestimmte: Viele Tonleitern, aber eben nicht alle Tonleitern des Quintenzirkel.
wohltemperiert gestimmte: Alle Tonleitern, manche reiner als andere.
gleichstufig gestimmte: Alle Tonarten gleich rein, aber mit geschärften Terzen.
Heutzutage sind die meisten Klaviere gleichstufig gestimmt, manche Orgeln und Cembali mitteltönig oder wohltemperiert.
rein:
rein
Chromatischer und diatonischer Halbton
In reiner Stimmung hat der diatonische Halbtonschritt ,,cis ,d die Grö0e von 112 Cent und der chromatische Halbtonschritt c ,,cis die Größe von 71 Cent.Ähnlich ist es bei der mitteltönigen Stimmung.
Bei der gleichstufigen Stimmung sind beide Halbtöne gleich, nämlich 100 Cent.
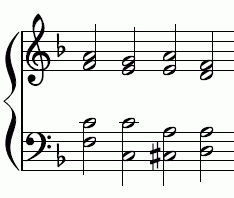
Rein:
Mitteltönig:
Gleichstufig:
Passus Duriuskulus
rein
Die Halbtöne im Bass sind teils
chromatisch (71 Cent und 92 Cent)
teils diatonisch (112 Cent).
gleichstufig
Dieselbe Melodie mal in C-Dur, mal in G-Dur
In C-Dur: h c ,e g ,a c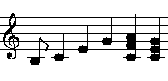
In G-Dur: h c ,e g a g
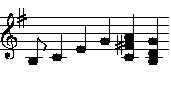
In G-Dur erklingt der Ton a höher als das ,a in C-Dur.
Spiele ,a in C-Dur (440 Hz) und a in G-Dur (445,5Hz) und beide und zusammen.
Dominantseptakkord und Tonika
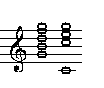rein
gleichstufig
In reiner Stimmung erklingt der Dominantseptakkord viel spannungsreicher als in gleichstufiger Stimmung!
mehr ...
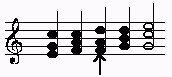
Kommafalle
Gerade Chöre, die rein intonieren, können in die Kommafalle tappen.
Der letzte Akkord ist im Vergleich zum ersten ein Komma tiefer. Nach zweilmaligen Singen hört man deutliche den Unterschied.
Beim Singen muss man beachten, dass das d im 3. (Akkord auf der II. Sufe) und 4. Akkord (Dominantakkord) sich ändert. Im 3. Akkord ist es ein Komma tiefer zu intonieren, im 4. Akkord wieder ein Komma höher. Das Absinken kann man vermeiden, wenn der Sopran tonal hört, also im 4. Akkord, im Dominantakkord, das d als reine Quinte zu g.
Erklärung ...
Unterschied von DIS und ES (Diaschisma)
Melodie: Vom Himmel hoch, da komm ich her.
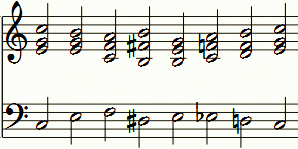In reiner Stimmung
Das Dis im 4. Akkord ist in reiner Stimmung um 20 Cent tiefer als das Es im 6. Akkord.
mehr ...
Der "Wolf" in der Mitteltönigen Stimmung
Spiele 1/4-mitteltönig die F-Dur- und die As-Dur-Kadenz:
Die As-Dur-Kadenz ist um fast einen halben Halbton verstimmt, denn statt "AS" erklingt das um 41 Cent höhere "Gis".
Mehr darüber
Satz: Friedrich Silcher
spiele erste Zeile in reiner Stimmung:
Spiele zweite Zeile in reiner Stimmung:
Ein aufmersamer Hörer teilte mir mit, dass in Takt 6 ein Akkord unrein klingt. Die Analyse ergab:
Hier sind in reiner Stimmung in g-Moll die Kadenzakkorde G-'B-D, C-'Es-G und D-,Fis-A rein. Bei der Modulation zu B-Dur (Takt 6 und Takt 13) mit den reinen Kadenzakkorden 'B-D-'F, 'Es-G-'B und 'F-A-'C erhöht sich der Ton C um ein syntonisches Komma zu 'C.
Hinweis: Durdreiklänge sind in Eulerschreibweise stets von der Form 1 ,3 5 oder '1 3 '5, Molldreiklänge von der Form 1 '3 5 oder ,1 3 ,5.
mehr ...
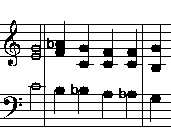
Der verminderte Septakkord
Beim verminderten Septakkord sind drei kleine Terzen übereinander gestapelt. Genauer: eine reine kleine Terz, dann eine kleine pythagoreische Terz und dann wieder eine reine kleine Terz.(Frequenzverhältnis: reine kleine Terz: 6/5 ≙ 316 Cent,kleine pythagoreische Terz: 32/27 ≙ 294 Cent.)
Beispiel (in Eulerschreibweise):
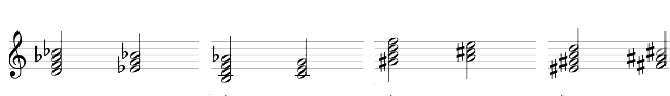
d 'f 'as ''ces. Auflösung nach 'Es-Dur: 'es g 'b ,h d f 'as. Auflösung nach C-Dur: c ,e g ,,gis ,h ,d f. Auflösung nach ,A-Dur: ,a ,,cis ,e ,,,eis ,,gis ,,h ,d. Auflösung nach ,,fis-Dur: ,,fis ,,,ais ,,cis
(Die Fortschreitung erfolgt über reine kleine Terzen:
Von 'Es-Dur nach C-Dur nach ,A-Dur und nach ,,Fis-Dur.
Denkbar wäre auch eine Fortschreitung im Quintenzirkel (siehe unten):
Von Es-Dur nach C-Dur nach A-Dur und nach Fis-Dur.)
Die hier verminderten Septakkorde in gleicher Lage:
Eulerschreibweise Frequenzen in Hertz Abstand von c in Cent d 'f 'as ''ces 297 356,4 422,4 506,9 204 520 814 1129 d f 'as ,h 297 352 422,4 495 204 498 814 1088 ,d f ,,gis ,h 293,3 352 412,5 495 182 498 773 1088 ,d ,,,eis ,,gis ,,h 293,3 343,8 412,5 488,9 182 457 773 1067Von Akkord zu Akkord erklingen jeweils zwei Töne gleich. Am Schluss ist der Akkord jedoch bis zu zwei Kommata tiefer.
Berechnung mit Schisma s = 2 Cent und syntonisches Komma k = 21,5 Cent:
,eis = f + s ⇒,,,eis = 'f + s - 3k. Unterschied 3k - s = 63 Cent (große Diesis).
,gis = as + s ⇒ 'as = ,,gis + s - 2k. Unterschied 2k - s = 41 Cent (kleine Diesis).
h = 'ces+s ⇒ ,,h = ''ces + s -2k. Unterschied 2k - s = 41 Cent (kleine Diesis).
Lediglich d und ,d unterscheiden sich nur um das syntonische Komma (21,5 Cent).
Dieselben Akkord nun quintverwandt
... und nicht mehr terzverwandt
Die vorkommenden Intervalle sind:
reine kleine Terz
(Frequenzverhältnis 6/5 entspricht 316 Cent)
pythagoreische kleine Terz
(Frequenzverhältnis 32/27 entspricht 294 Cent, ein Terzkomma tiefer)
übermäßige Sekunde
(Frequenzverhältnis 75/64 entspricht 274 Cent, noch ein Terzkomma tiefer)
Tonart Eulerschr. Abst. von c in Cent Intervall in Cent
Es-Dur as 'ces ,d f 792 1108 182 498 316 294 316
,g b es 680 996 294
C-Dur 'as ,h d f 814 1088 204 498 274 316 294
g c ,e 702 0 386
A-Dur ,gis h d 'f 794 1110 204 520 616 294 316
a ,cis e 906 92 408
Fis-Dur gis h 'd ,eis 816 1110 225 500 294 316 274
,ais cis fis 998 114 612
Fast reine Prim 440 Hz und 440,5086 Hz
Schwebungen bei Schisma(2 Cent)-Differenz
Beachte die Schwebungen!
mehr ...