Die Homepage von Joachim Mohr
Das Siebeneck
Wenn hier vom Siebeneck die Rede ist, dann ist das ebene, regelmäßige Siebeneck gemeint.I Die Konstruierbarkeit des Siebenecks
Wie Carl Friedrich Gauß 1804 bewies, lassen sich nur ganz bestimmte (regelmäßige) Vielecke mit Zirkel und Lineal konstruieren:Ein n-Eck kann man nur dann mit Zirkel und Lineal konstruieren,
- wenn n eine Potenz von 2 ist oder
- wenn n das Produkt einer Potenz von 2 mit verschiedenen Fermatschen Primzahlen ist.
- 220+1 =3,
- 221+1 = 5,
- 222+1 = 17,
- 223+1 = 257 und
- 224+1 = 65537
Zu den mit Zirkel und Lineal konstrueirbaren Vielecken gehören:
- a) Das 4-Eck, 8-Eck, 16-Eck, ...
- b) Das 3-Eck, 6-Eck, 12-Eck, ...
- c) Das 5-Eck, 10-Eck, 20, Eck
- b) und c) kombiniert: Das 15-Eck, 30-Eck, 60-Eck, ...
- d) Das 17-Eck, 34-Eck, 68-Eck, ...
- u.s.w.
Halten wir fest: Das Siebeneck ist nicht mit Zirkel und Lineal konstruierbar.
II Konstruktion des Siebenecks
Die Konstruktion des Siebenecks ist nicht mit Zirkel und Lineal möglich. Wenn man aber zuläßt, dass Strecken auf dem Lineal markiert werden, dann ist es möglich. Man spricht dann von Neusis-Konstruktionen. (Siehe WP, dort nur numerische Verifikation.)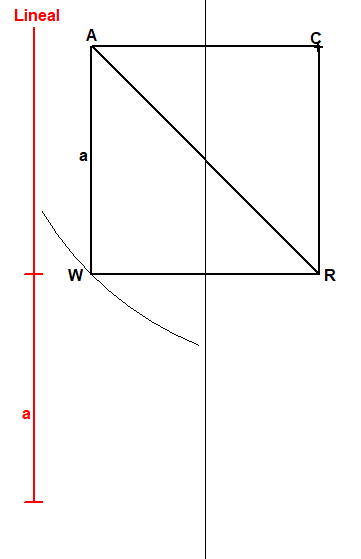
Zeichne das Quadrat ACRW mit der Seitenlänge a und um C den Kreis durch W (hier nur angedeutet)
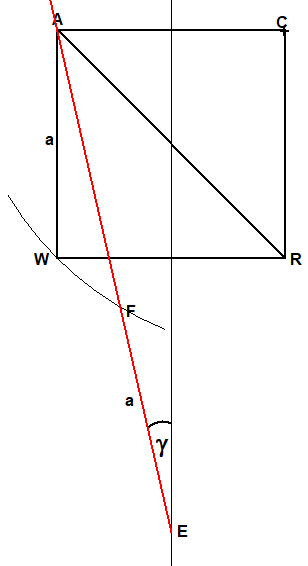
Lege das Lineal so an, dass es durch A geht und die Markierungen der Strecke a auf dem Kreis um C mit Radius CW und der Mittelsenkrechten von AC liegt. Der Winkel, den das Lineal mit der Mittelsenkrechten von AC bildet, hat die Größe
1 360° 360° γ=—·————. Damit läßt sich das Siebeneck mit dem Mittelpunktswinkel ———— konstruieren. 4 7 7
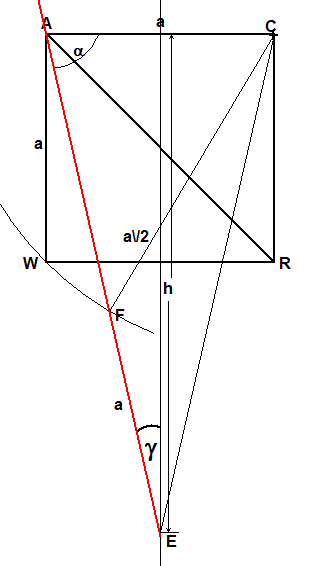
Beweis: (siehe Johnson, C. "A Construction for a Regular Heptagon." Math. Gaz. 59, 17-21, 1975.) Im Webarchiv 28.5.2023
Im rechtwinkligen Dreieck mit der Seite x=AE, der Höhe h
mit dem Winkel γ gilt
a a
sin(γ)=—:x ⇒ x = ———————— (1)
2 2sin(γ)
Im Dreieck CFE mit CE=x und FE=a gilt nach dem Kosinussatz
2 2 2 2 2
2a = a + x - 2axcos(2γ) ⇒ a - x + 2axcos(2γ) = 0 (2)
2
(1) in (2) und durch a diviert ergibt eine Gleichung nur mit γ:
1 cos(2γ) 2
1 - —————————— + ——————— = 0 Mit cos(2γ)=1-2sin (γ) folgt:
2 sin(γ)
4sin (γ)
3 2
8sin (γ)-4sin (γ)-4sin(γ)+1=0 (*)
Diese Gleichung wird erfüllt von
1 360°
γ = —·———— (die beiden anderen Lösungen von (*)
4 7
5 360° 3 360°
γ = —·———— und γ = - —·———— entfallen.)
4 7 4 7
Neusis-Konstruktion des 7-Ecks nach Crockett Johnson
Siehe The Mathematical Gazette Vol. 59, No. 407 (Mar., 1975), pp. 17-21 Published By: The Mathematical Association.
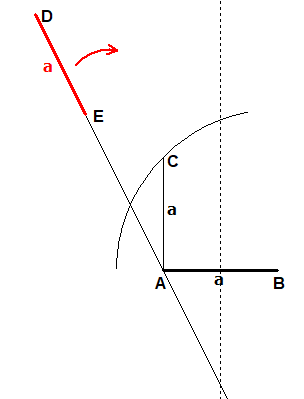
Zeichne AB=a und AC=a senkrecht auf AB und einen Kreis mit Mittelpunkt in B durch C.
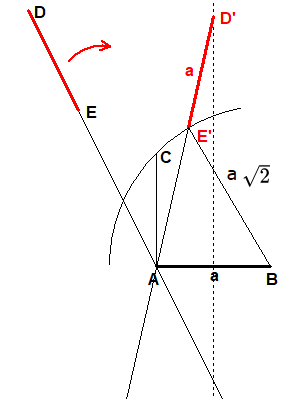
Passe das Lineal so ein, dass D (in der zweiten Zeichnung als D' bezeichnet) auf der Mittelsenkrechten von AB und E (dann als E' bezeichnet) auf dem Kreis um B durch C zu liegen kommt und das Lineal außerdem noch durch A geht.
Das Dreieck ABD' ist gleichschenklig mit Grundseite AB=a. Weiter ist E'D'=a und BE'=BC=a√2.
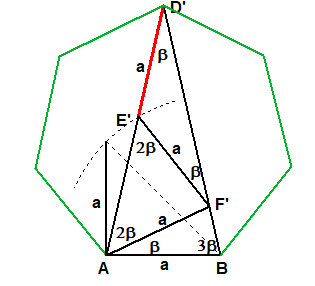Wir zeichen noch F' auf BD' mit E'F'=a ein.
Durch eine komplizierte Rechnung kann man zeigen, dass AF'=a ist.
Dann erhalten wir das Dreieck ABD' mit den Winkeln
∡D'AB=3β, ∡ABD'=3β und ∡AD'B=β.
Nach dem Winkelsummensatz im Dreieck ist 7β=180°, also β=1/7·180°.
Die Ecken des 7-Ecks liegen auf dem Umkreis von ABD'.
III Die Konstruktion des Siebenecks mit Hilfe der Dreiteilung eines Winkels und einer Kubikwurzel
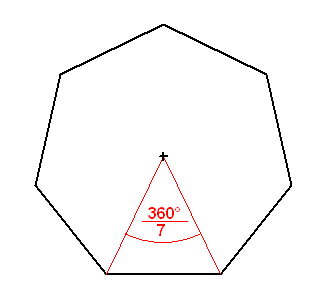
Das Problem der Konstruktion des Siebenecks ist:
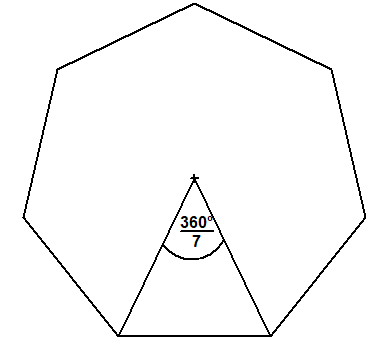
Wie kann ich seinen Mittelpunktswinkel 360°/7 konstruieren?
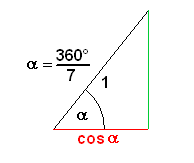
Da cos(360°/7) nur als Lösung einer Gleichung dritten Grades darstellbar ist, ist der Winkel 360°/7 nicht mit Zirkel und Lineal allein konstruierbar.
Andererseits ist hier die Lösung der Gleichung dritten Grades nach der Formel von Cardano mit Hilfe der Dreiteilung eines Winkels und der Kubikwurzel darstellbar. Im Folgenden konstruieren wir einen bestimmten Winkel mit Zirkel und Lineal. Nach der Dreiteilung dieses Winkels und der Ermittlung einer Kubikwurzel - wie auch immer (nicht mit Zirkel und Lineal möglich) - ist die Fertigstellung der Konstruktion des Siebenecks mit Zirkel und Lineal ausführbar.
Behauptung: x = cos(360°/7) ist eine Lösung der Gleichung 8x3 + 4x2 - 4x - 1 = 0
Beweis:
2 3
Mit cos(2α) = 2cos α - 1 und cos(3α) = 4cos α - 3 cosα folgt für x = cosα
2 3 3 2
cosα+ cos(2α) + cos(3α) = x + 2x -1 + 4x - 3x = 4x + 2x - 2x - 1
1
Für α = 360°/7 ist cosα+ cos(2α) + cos(3α) = - - (* Nachweis unten)
2
360° 3 2 1
und somit gilt für x = cos——— die Gleichung 4x + 2x - 2x - 1 = - -
7 2
3 2
oder 8x + 4x - 4x - 1 = 0
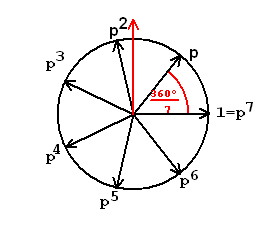
Beweis von (*) (Beitrag in de.sci.mathematik
von Thomas Nordhaus und Wolfgang Kirschenhofer Februar 2008)
360° iα 7
für α= ——— und p = cis(α) = e folgt mit p = 1
7
7
2 3 4 5 6 1 - p
1 + p + p + p + p + p + p = ————— = 0
1 - p
Aus Symmetriegründen sind die Realteile von
6 2 5 4 3
p und p , p und p sowie von p und p gleich und somit ist
2 3 3 2
1 + Re(p) + Re(p ) + Re(p ) + Re(p ) + Re(p ) + Re(p) = 0
1 + 2cosα + 2cos(2α) + 2cos(3α) = 0
1
=> cosα + cos(2α) + cos(3α) = - -
2
Weitere Werte der trigonometrischen Funktionen siehe hier.
Berechnung von x = cos(360°/7) als Lösung 8x3 + 4x2 - 4x - 1 = 0 nach Cardano
(Siehe Beispiel b)
Gesucht ist die Lösung der Gleichung
3 2
8x +4x -4x-d=0
Substitution x=z-b/(3*a) führt auf
3 7 7
z - ——z - ——— =0
12 216
Rechnung:
q 2 p 3 49
d= (-) + (-) = - ————
2 3 6912
Dann ist
3 q - 7 7 -
u = - - + \/d = x+y*i für x=——— und y= ———\/3
2 432 144
Mit
-
α = arctan(y/x)=arctan(3\/3)
———————
3 / 7 - α
ergibt sich z = 2\/ ———\/7 ·cos(-)
216 3
———————
360° 3/ 7 - α 1
und somit x = cos(———) = 2\/ ———\/7 ·cos(-) - -
7 216 3 6
Rechnung mit TTMathe (Rechenblatt)
Lösung von ax^3+bx^2-cx+d=0
a=8
b=4
c=-4
d=-1
wird auf die red. kub. Gl.
z^3+p*z+q=0 zurückgeführt.
Subst. x=z-b/(3*a)
p=c/a-(b/a)^2/3=-7/12
q=2/27*(b/a)^3-1/3*(b/a)*(c/a)+d/a=-7/216
Lösung von z^3 + pz + q = 0
nach Cardano
d=(q/2)^2+(p/3)^3=-49/6912
u^3=-q/2+d^(1/2)=x+y*i für x=7/432 und y=7/144*sqrt(3)
y/x=3*sqrt(3)
al=arctan(3*sqrt(3)) =1,380670723
Im Bogenmaß al=57,295779513°
z=2*cbrt(7/216*sqrt(7))*cos(al/3)=0,790156469
x=z-b/(3*a)=0,623489802
Probe:
phi=arccos(x)=2/7*Pi
phi=360°/7=2/7*Pi
Konstruktion des Siebenecks nach dieser Rechnung
- Mit Zirkel und Lineal kann man die Strecke a und den Winkel α konstruieren mit:
7 - - a= ———\/7 und tanα=3\/3 216 - Wie auch immer konstruiere man den Winkel β und die 3. Wurzel
α 3 - β = - und b = \/a 3 - konstruiere mit Zirkel und Lineal
x=2·b·cosβ - 1/6
- Konstruiere schließlich mit Zirkel und Lineal das Siebeneck mit dem Mittelpunktswinkel
360° φ = ——— mit cosφ = x 7
Weitere Berechnungen am Siebeneck
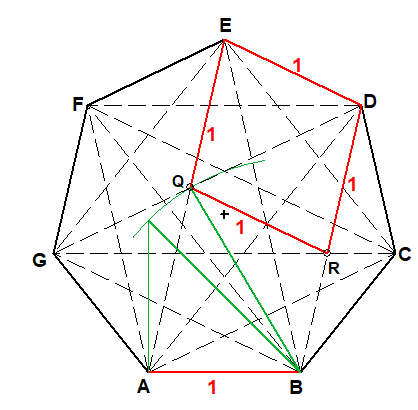
Der Innenwinkel im 7-Eck beträgt: α=5/7·180°≈128,57°
Das Siebeneck hat zwei unterschiedlich lange Diagonalen.
AE=d1 (von A zur nächst 3. Ecke) und AC=d2 (zur nächst 2. Ecke)
Im Dreieck ABC gilt nach dem Kosinussatz d22=1+1-2cos(α)=2(1-cos(α)).
——————————
⇒d2=√2(1-cos(α) ≈1,8019 (α=5/7·180°)
Im Dreieck AEB ist der Winkel bei A gleich
3 1 1
β=——·180° ⇒ d1=—·—————— ≈ 2,2469 (β=3/7·180°)
7 2 cos(β)
Es gilt: d1+d2=d1·d2 (Beweise: siehe unten)
Q sei der Schnittbunkt der langen Digonalen EA
mit der kurzen Diagonalen DG
und R der Schnittbunkt der langen Digonalen GC
mit der kurzen Diagonalen DB.
Dann ist EQRD eine Raute mit der Seitenlänge 1 und den Innenwinkeln 3/7·180° und 4/7·180°.
Die kleinere Diagonale der Raute hat die Länge DQ=√2-cos(3/7·180°)≈1,2470
Und außerdem mißt BQ=√2
Autor: Dan Lawson
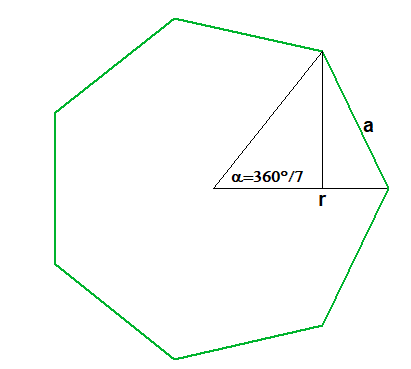Nach dem Kosinussatz gilt: a2=2r2(1-cos(α))
—
2√2
Für a=4 folgt r=————————— = 4,593459431
————————
√1-cos(α)
Sei M der Mittelunkt des Umkreises und AB die Endpunkte der Seite a (MA waagrecht).
Dann ist α=∡AMB=360°/7 und ∡MAB=∡MBA=5/4*1/7*360°
Die Kosinuswerte des Sieneecks berechnen sich (siehe Kosinuswerte (unten):
cos(180°·k/7) (k=1,3,5) 8x^3-4x^2-4x+1=0
cos(180°/7)= 1/12*((-28+84*I*sqrt(3))^(2/3)+28+2*(-28+84*I*sqrt(3))^(1/3))/(-28+84*I*sqrt(3))^(1/3)
cos(180°·3/7) =-1/24*((-28+84*I*sqrt(3))^(2/3)+28-4*(-28+84*I*sqrt(3))^(1/3)+I*sqrt(3)*(-28+84*I*sqrt(3))^(2/3)-28*I*sqrt(3))/(-28+84*I*sqrt(3))^(1/3)
cos(180°·5/7)=1/24*(-(-28+84*I*sqrt(3))^(2/3)-28+4*(-28+84*I*sqrt(3))^(1/3)+I*sqrt(3)*(-28+84*I*sqrt(3))^(2/3)-28*I*sqrt(3))/(-28+84*I*sqrt(3))^(1/3)
cos(360°·k/7) (k=2,4) 8x^3+4x^2-4x-1=0
cos(180°·2/7)=1/12*((28+84*I*sqrt(3))^(2/3)+28-2*(28+84*I*sqrt(3))^(1/3))/(28+84*I*sqrt(3))^(1/3)
cos(180°·4/7)=-1/24*((28+84*I*sqrt(3))^(2/3)+28+4*(28+84*I*sqrt(3))^(1/3)+I*sqrt(3)*(28+84*I*sqrt(3))^(2/3)-28*I*sqrt(3))/(28+84*I*sqrt(3))^(1/3)
——————————
/ —
Mit w=∛-28+84i·√3
2
180° 1 w + 28 +2w
cos(1·————)= —— ——————————
7 12 w
2
180° 1 w + 28 -2w
cos(2·————)= —— ——————————
7 12 w
2 — 2 —
180° 1 w + 28 -4w+i√3w -28i√3
cos(3·————)= - —— ——————————————————————
7 24 w
2 — 2 —
180° 1 w + 28 +4w+i√3w -28i√3
cos(4·————)= - —— ——————————————————————
7 24 w
2 — 2 —
180° 1 - w - 28 +4w+i√3w -28i√3
cos(5·————)= —— ——————————————————————
7 24 w
2 — 2 —
180° 1 - w - 28 -4w+i√3w -28i√3
cos(6·————)= —— ——————————————————————
7 24 w
180° 180°
Es ist cos(6·————)= - cos(1·————)
7 7
180° 180°
cos(5·————)= - cos(2·————)
7 7
180° 180°
cos(4·————)= - cos(3·————)
7 7