Joachim Mohr Mathematik Musik

Rationale Trigonometrie Version 2

Am 11.01.2007 erläuterte Prof. Dr. Frank Loose die "Divine Proportions" von N. Wildberger. Für den Ersatz für den Abstand d und den Winkels α wird mit der Quadranz Q = d² und der Spreizung s = sin²(α) gerechnet,

Die trigonometrischen Größen lassen sich dann ganz ohne die transzendent Funktionen sin, cos, tan, arcsin, arccos und arctan berechnen.

Dieser Beitrag verwendet die Ideen von Wildberg mit klassischen Bezeichnungen. Das Ziel ist, alle berechneten Größen durch die Ausgangsgrößen mit Hilfe der Grundrechenarten und der Quadratwurzel darzustellen. Auf die Begriffe Quadranz und Spreizung wird hierbei verzichtet. Es ist jedoch offenkundig, dass mit den Quadratwurzeln dieser Größe gerechnet wird.

Die fünf Wildberger-Regeln

I) Die Tripel-Regel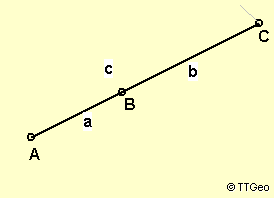

      ——     ——         ——
Für a=AB, b= BC und c = AC gilt:

A,B,C kollinear <=> a + b = c

                      2   2   2 2     4   4   4
                <=> (a + b + c ) = 2(a + b + c )

II) Satz von Pythagoras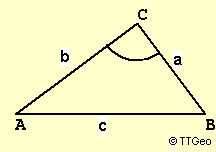
Satz des Pythagoras

      ——    ——       ——
Für a=BC, b=AC und c=AB gilt:

                                2   2    2
Dreieck rechtwinklig bei C <=> a + b  = c

III) Sinussatz

IV) Kreuzgesetz

Ich möchte dies am folgendem Beispiel erläutern:

Beispiel: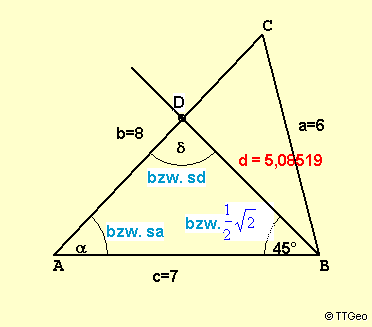

Im Dreieck ABC mit a=6, b=8 und c=7 wird an AB in B ein Winkel von 45° angelegt. Der freie Schenkel dieses Winkels schneidet AC in D.

Es soll die Länge von BD berechnet werden.

Bei der Klassischen Lösung wird der Kosinussatz

zur Berechnung des Winkels α verwendet ...

 2    2   2
a  = b + c  - 2bc·cos(α)

             2  2  2
            b +c -a)   11
=> cos(α) = ———————— = —— => α = 46,567
            2*b*c      16

=> δ=180° - 45° - α = 88,433°

... und der Sinusssatz zur Berechnung von d:

  d        c
—————  = —————— =>  d = 5,08519
sin(α)   sin(δ)

Rechnung ohne trigonometrische Funktionen

Setzte: sa=sin(α), sb=sin(45°) und sd=sin(δ).

        ca=cos(α), cb=cos(45°) und cd=cos(δ).

            2     2
Dann gilt sa  + ca  = 1 etc.

Nach dem Kosinusssatz ist:

 2    2   2                  11       2   135
a  = b + c  - 2bc·ca => ca = —— und sa =  ———
                             16           256

Klassisch wird nun der dritte Winkel δ aus α und 45° berechnet.

Nach Wildberger Tripelspreiz-Regel kann nun sd  berechnet werden:

   2    2    2 2       4    4     4       2  2  2
(sa + sb + sd )  = 2(sa + sb  + sd ) + 4sa sb sd

      2  135       2   1
mit sa = ——— und sb  = -   => sd = 3/32*sqrt(30)+11/32*sqrt(2)
         256           2

und schließlich nach dem Sinusssatz (Spreizgesetz):

    sa    7*sqrt(135)/16                    14*sqrt(135)        135          33
d=c·——  = ——————————————————————————— = ————————————————————— = ———sqrt(2) - ——sqrt(30)
    sd    3/32*sqrt(30)+11/32*sqrt(2)   3*sqrt(30)+11*sqrt(2)    2            2