Trigonometrie ohne trigonometrische Funktionen

Oder: Eigentlich hätten unsere Vorfahren bei Vermessungen auf die aufwendigen trigonometrische Tafen verzichten können.

Oder: Hätten die alten Griechen den Winkel mit einem andern Maß gemessen, wäre die Dreiteilung eines Winkels nie ein Problem gewesen.

Am 11.01.2007 erläuterte Prof. Dr. Frank Loose, Tübingen, die "Divine Proportions" von N. Wildberger. Für den Ersatz für den Abstand d und den Winkels α wird mit der Quadranz Q = d² und der Spreizung s = sin²(α) gerechnet. Wildberger entwickelt daraus eine "rationale Trigonometrie".

Die trigonometrischen Größen lassen sich dann ganz ohne die transzendent Funktionen sin, cos, tan, arcsin, arccos und arctan berechnen.

Dieser Beitrag verwendet die Ideen von Wildberger mit klassischen Bezeichnungen. Das Ziel ist, alle berechneten Größen durch die Ausgangsgrößen mit Hilfe der Grundrechenarten und der Quadratwurzel darzustellen. Auf die Begriffe Quadranz und Spreizung wird hierbei verzichtet. Es ist jedoch offenkundig, dass mit den Quadratwurzeln dieser Größe gerechnet wird.

Wozu soll das gut sein? Dazu möchte ich zwei Argumente vorbringen.

1. Jedem Hochschullehrer fällt es in Anfängervorlesungen schwer, die trigonometrischen Funktionen einzuführen. Manche definieren die Sinusfunktion gleich durch eine Reihe. Und das Bogenmaß über die Länge einer rektifizierbaren Kurve zu definieren ist auch nicht gerade trivial.

2. In der Vermessungslehre auf Grundlage der ebenen Trigonometrie mußten unsere Vorfahren mit ausgefeilten Tabellenwerten arbeiten.

Hier soll gezeigt werden: Es geht auch elementarer. Die Grunrechenarten und das Ziehen der Quadratwurzel genügt.

Grundgrößen

Wir gehen davon aus, dass wir in unserer Ebene alles mit Zirkel und Lineal konstruieren können. Die Länge d von Strecken kann als reelle Zahl gemessen werden. Rechte Winkel können konstruiert werden. Wir beschränken uns hier auf die Innenwinkel von Dreiecken.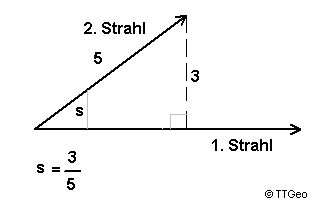

Da wir auf trigonometrische Funktionen und Ihre Umkehrfunktionen verzichten wollen, wird der "Winkel" zweier Halbgeraden durch das Maß s (s wie "Sinus") gekennzeichnet. s entspricht dem Sinus. Zu jedem Winkel muß noch vermerkt werden, ob er spitz oder stumpf ist. Die Messung kann man der Zeichnung entnehmen: Man fällt das Lot von einem Punkt des zweiten Strahls auf den ersten und berechnet "Gegenkathete" dividiert durch "Hypotenuse". Liegt der Schnittpunkt des Lotes auf dem ersten Strahl handelt es sich um einen spitzen Winkel, im anderen Fall (der Schnittpunkt liegt auf der Verlängerung des Strahls in die andere Richtung) heißt der Winkel stumpf.

Beispiele

     

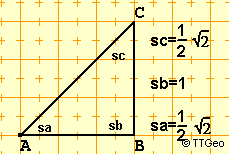
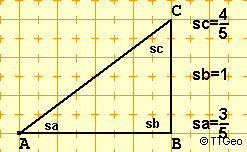
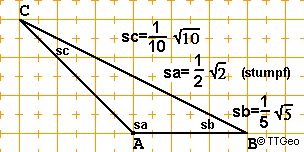
Regeln für Berechnungen

Wir wollen nun ebene Trigonometrie betreiben, wie sie seit Jahrtausenden in der Vermessungslehre betrieben wurde und zeigen: Es geht auch ohne trigonometrische Funktionen. Man hätte also - vor dem Taschenrechner- oder Computerzeitalter - auf trigonometrische Tafeln vollständig verzichten können.

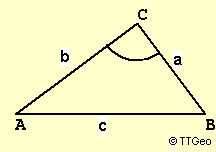
Satz de Pythagoras —— —— —— Für a=BC, b=AC und c=AB gilt: 2 2 2 Dreieck rechtwinklig bei C <=> a + b = c

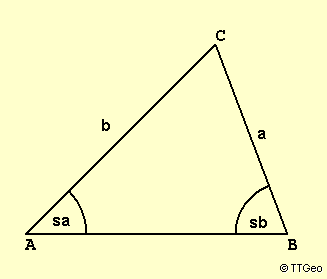
Sinussatz sa sb —— = —— a b

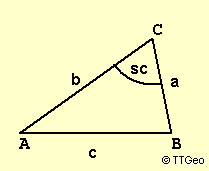
Kosinussatz ——————— 2 2 2 / 2 c = a + b - 2·a·b·cc, wobei cc = ± \/ 1 - sc , wobei hier "+" beim spitzen Winkel sc und "-" beim stumpfen Winkel sc gilt.

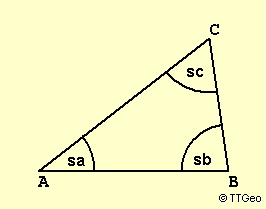
Winkelberechnungssatz Wenn zwei Winkel gegeben sind, kann der dritte wie beim Winkelsummensatz berechnet werden. 2 2 sc = sa·sqrt(1-sb ) + sb*sqrt(1-sa ) (Dank an Almut Eisenträger für die Herleitung der Formel in de.sci.mathematik)

Beispiel für eine trigonometrische Berechnung ohne trigonometrische Funktionen.

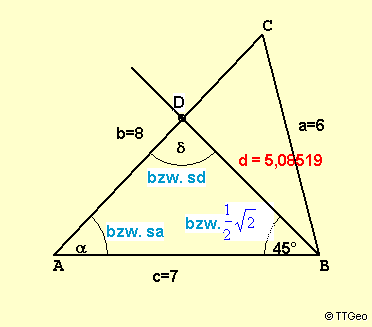Im Dreieck ABC mit a=6, b=8 und c=7 wird an AB in B ein Winkel angelegt, wie ihn im Quadrat die Diagonale mit einer Seite bildet, (klassisch: eine Winkel von von 45°). Der freie Schenkel dieses Winkels schneidet AC in D. Es soll die Länge von BD berechnet werden. Bei der Klassischen Lösung wird der Kosinussatz zur Berechnung des Winkels α verwendet ... 2 2 2 a = b + c - 2bc·cos(α) 2 2 2 b +c -a) 11 => cos(α) = ———————— = —— => α = 46,567° (transzendent) 2*b*c 16 ... und der Winkelsummensatz α + δ + 45° = 180° => δ=180° - 45° - α = 88,433° (transzendent) ... sowie der Sinussatz zur Berechnung von d: d c ————— = —————— => d = 5,08519 (transzendent ???) sin(α) sin(δ) (Angabe exakt nicht möglich)

Rechnung ohne trigonometrische Funktionen

Es werden die Größen sa, sb, sd, ca, cb und cd verwendet.

Zum besseren Verständnis der Hinweis:

        sa=sin(α), sb=sin(45°) und sd=sin(δ).

        ca=cos(α), cb=cos(45°) und cd=cos(δ).

Nach dem Kosinussatz ist:

 2    2   2                  11       2   135       2    2
a  = b + c  - 2bc·ca => ca = —— und sa =  ———, da sa + sb = 1.
                             16           256

Nach dem Winkelberechnungssatz kann nun sd  berechnet werden:

sd = sa·sqrt(1-sb^2) + sb·sqrt(1-sa^2)

mit sa = 3/16·sqrt(15) und sb = 1/2·sqrt(2) folgt sd = 3/32·sqrt(30)+11/32·sqrt(2)

und schließlich nach dem Sinussatz:

    sa    7*sqrt(135)/16                    14*sqrt(135)        135          33
d=c·——  = ——————————————————————————— = ————————————————————— = ———sqrt(2) - ——sqrt(30)
    sd    3/32*sqrt(30)+11/32*sqrt(2)   3*sqrt(30)+11*sqrt(2)    2            2

also d ist algebraisch und nicht transzendent.