Joachim Mohr Mathematik Musik
Es gibt Konstruktionen, die nicht mit Zirkel und Lineal möglich sind. Seit der Antike sind jedoch Konstruktionen möglich, die mit einem Lineal, auf dem eine Strecke markiert ist, also durch eine "Einschiebung".
Neusis-Konstruktionen
Entnommen einer Arbeit von K.Schmidt 2023
Bei der Neusis-Konstruktion (νεῦσις=neusis griechich Neigung oder Einschiebung) wird ein Lineal verwendet, bei der eine Strecke a markiert ist. Das Lineal wird nun so gelegt, dass die Endpunkte der Strecke a auf Geraden oder Kreisen liegt und außerdem das Lineal noch durch einen weiteren Punkt geht. Es handelt sich hierbei um eine Näherungsvorgang, der mit einer gewissen Übung schnell mit Augenmaß zu Ende geführt wird.Dreiteilung des Winkels nach Archimedes
Die Dreiteilung von manchen Winkel ist nicht mit Zirkel und Lineal möglich. Wenn man aber zuläßt, dass Strecken auf dem Lineal markiert werden, dann ist es möglich. Man spricht dann von Neusis-Konstruktionen. (Quelle WP)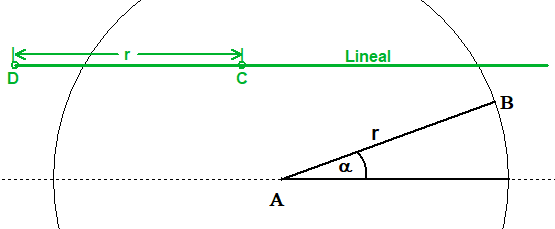
Gegeben ist der Winkel α mit einem Schenkel AB, dessen Länge r gleich dem Radius des Kreises durch A ist.
Man verwendet nun ein Lineal, bei dem die Strecke r=DC markiert ist.
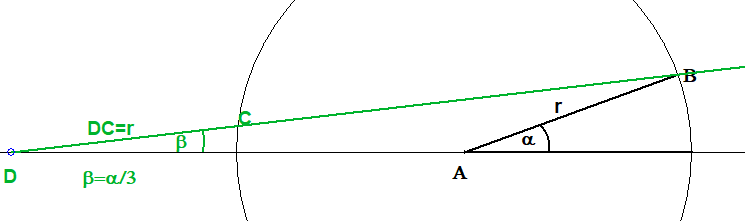Nun wird das Lineal so verschoben, dass
(1) D auf der Verlängerung des anderen Schenkels des Winkels α liegt und
(2) C auf dem Kreis liegt und
(3) das Lineal durch B geht.
Behauptung:
Dann ist β = ∡ADC = α/3.
Beweis: Der Beweis benötigt nur den Winkelsummensatz im Dreieck und Berechnung mit Winkeln im gleicheitigen Dreieck.
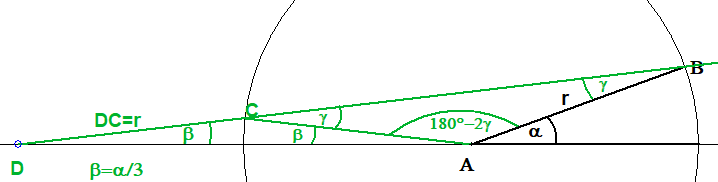
AC=DC. Das Dreieck ADC ist also gleischenklig. Der Winkel in diesem Dreieck bei C ist also 180°-2β.
Der Nebenwinkel ist dann γ=180°-(180°-2β)=2β. Dieser Winkel γ tritt auch bei B auf.
Und der Winkel bei A ist also 180°-2γ.
Dann ist 180°=β+(180°-2γ)+α also
α=2γ-β=4β-β=3β ⇒ β=α/3. ✅
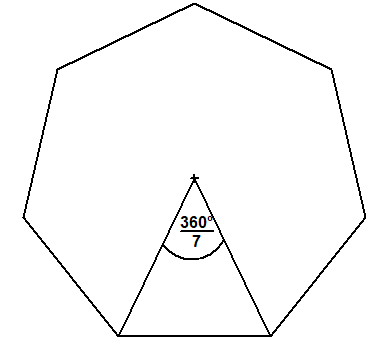
Konstruktion des Neunecks
Der Winkel von 60° wird hier dreigeteilt in α=20°
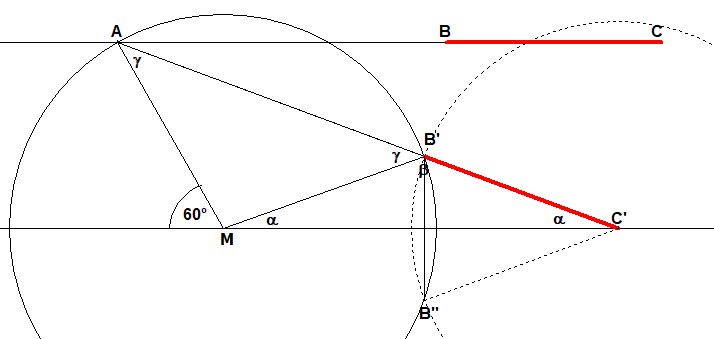
Zeichne in einen Kreis einen Mittelpunktswinkel von 60° und verwende ein Lineal, dessem Markierung BC die Länge des Kreisradiuses hat.
Das Lineal wird so gelegt, dass
(1) C zu C' auf einem verlängertem Durchmesser des Kreises liegt und
(2) B zu B' auf dem Kreis zu liegen kommt und außerdem noch
(3) durch A geht.
Wir zeigen, dass der Winkel B'C'B'' sich zum Mittelpunktwinkel 360°:9=40° des Neunecks ergibt.
Nachweis:
Im gleichschenkligen Dreieck MB'C' errechnet sich
β=180°-2α ⇒ γ=180°-β=180°-(180°-2α)=2α
⇒ ∡B'MA=180°-2γ=180°-4α
Der gestreckte Winkel von 180° bei M ist die Summe von drei Winkeln:
60°+(180°-4α)+α=180°
⇒ 3α=60° ⇒ α=20°
⇒ ∡C'B'B''=40° = Mittelpunktwinkel des Neunecks.
Würfelverdopplung nach Archimedes
Hat ein Würfel die Kantenlänge a, so hat der Würfel mit doppelten Volumen die Länge c=a∛2. Die Konstruktion von c aus a ist allein mit Zirkel und Lineal nicht möglich (Delisches Problem). Wenn man aber zuläßt, dass Strecken auf dem Lineal markiert werden, dann ist dies möglich. Man spricht dann von Neusis-Konstruktionen. (Quelle WP).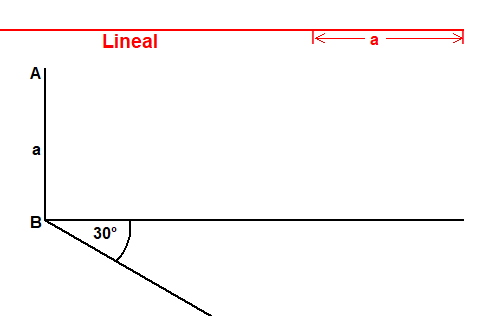
An die Strecke AB=a zeichnet man in B eine Senkrechte und nach unten einen Winkel von 30°.
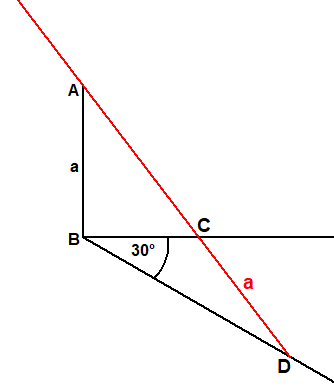
Dann legt man eine Lineal mit der Markierung a=CD folgndermaßen an.
(1)Das Lineal geht durch A
(2)Die Schenkel des Winkels 30° schneiden das Lineal in CD=a.
Dann hat die Strecke AC die Länge c=a∛2.
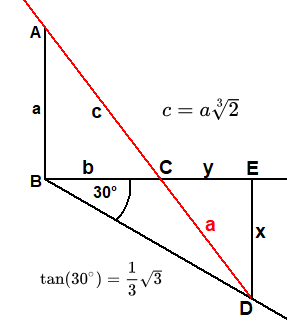Beweis:
Die Dreieck ABC und DEC sind ähnlich.
2
a
⇒x:a=a:c ⇒ x =——
c
ab
y:b=a:c ⇒ y=——
c
2 2
x a a
tan(30°) = ——— = ———————— = ———————
b+y ab b(a+c)
c(b+———)
c
4
1 1 a 4 2 2
Mit tan(30°)=—— folgt — = ———————— ⇒ 3a =b (a+c)
√3 3 2 2
b (a+c)
2 2 2
Nach Pythagoras b = c -a
2 2 2 4
⇒ (c -a )(a+c) =3a
2 2 2 2 4
⇒(c -a )(a +2ac +c )=3a
2 2 3 4 4 3 2 2 4
⇒ c a +2ac +c -a -2a c -a c =3a
3 4 4 3 4
⇒ 2c a+c -a - 2a c=3a
3 4 4 3
⇒ 2c a + c =4a +2a c
3 3 3 3
⇒ c (2a+c)=2a (2a+c) ⇒ c = 2a ⇒ c=a∛2.
Konstruktion des Siebenecks
Das Siebeneck ist nicht mit Zirkel und Lineal möglich. Wenn man aber zuläßt, dass Strecken auf dem Lineal markiert werden, dann ist es möglich. Man spricht dann von Neusis-Konstruktionen. (Quelle WP, dort nur numerische Verifikation.)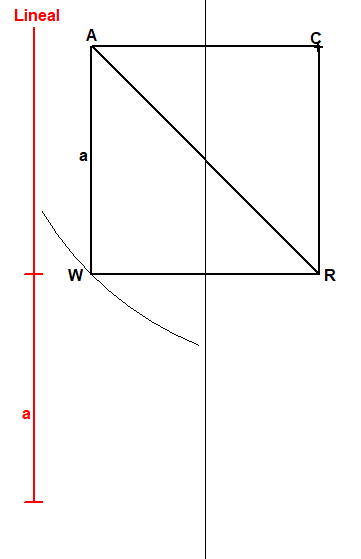
Zeichne das Quadrat ACRW mit der Seitenlänge a und um C den Kreis durch W (hier nur angedeutet)
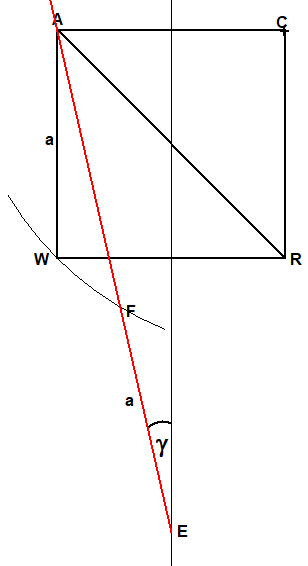
Lege das Lineal so an, dass es durch A geht und die Markierungen der Strecke a auf dem Kreis um C mit Radius CW und der Mittelsenkrechten von AC liegt. Der Winkel, den das Lineal mit der Mittelsenkrechten von AC bildet, hat die Größe
1 360° 360° γ=—·————. Damit läßt sich das Siebeneck mit dem Mittelpunktswinkel ———— konstruieren. 4 7 7
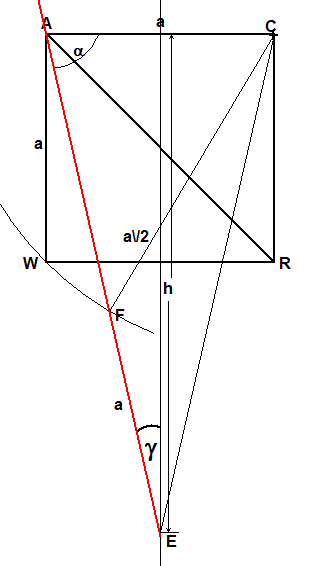
Beweis: (siehe Johnson, C. "A Construction for a Regular Heptagon." Math. Gaz. 59, 17-21, 1975.) Im Webarchiv 28.5.2023
Im rechtwinkligen Dreieck mit der Seite x=AE, der Höhe h
mit dem Winkel γ gilt
a a
sin(γ)=—:x ⇒ x = ———————— (1)
2 2sin(γ)
Im Dreieck CFE mit CE=x und FE=a gilt nach dem Kosinussatz
2 2 2 2 2
2a = a + x - 2axcos(2γ) ⇒ a - x + 2axcos(2γ) = 0 (2)
2
(1) in (2) und durch a diviert ergibt eine Gleichung nur mit γ:
1 cos(2γ) 2
1 - —————————— + ——————— = 0 Mit cos(2γ)=1-2sin (γ) folgt:
2 sin(γ)
4sin (γ)
3 2
8sin (γ)-4sin (γ)-4sin(γ)+1=0 (*)
Diese Gleichung wird erfüllt von
1 360°
γ = —·———— (die beiden anderen Lösungen von (*)
4 7
5 360° 3 360°
γ = —·———— und γ = - —·———— entfallen.)
4 7 4 7
Neusis-Konstruktion des 7-Ecks nach Crockett Johnson
Siehe The Mathematical Gazette Vol. 59, No. 407 (Mar., 1975), pp. 17-21 Published By: The Mathematical Association.
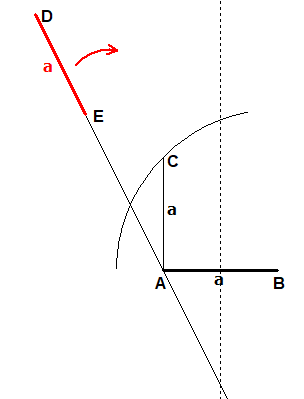
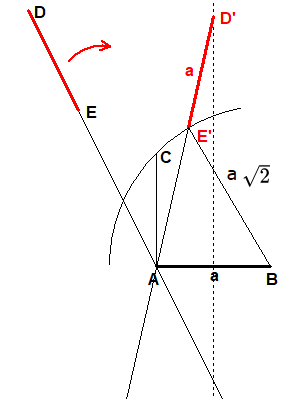
Zeichne AB=a und AC=a senkrecht auf AB und einen Kreis mit Mittelpunkt in B durch C.
Passe das Lineal so ein, dass D (in der zweiten Zeichnung als D' bezeichnet) auf der Mittelsenkrechten von AB und E (dann als E' bezeichnet) auf dem Kreis um B durch C zu liegen kommt und das Lineal außerdem noch durch A geht.
Das Dreieck ABD' ist gleichschenklig mit Grundseite AB=a. Weiter ist E'D'=a und BE'=BC=a√2.
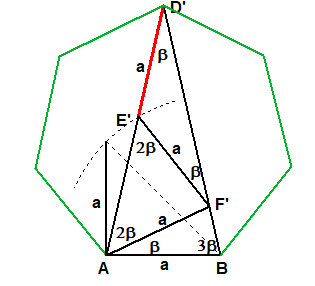Wir zeichen noch F' auf BD' mit E'F'=a ein.
Durch eine komplizierte Rechnung kann man zeigen, dass AF'=a ist.
Dann erhalten wir das Dreieck ABD' mit den Winkeln
∡D'AB=3β, ∡ABD'=3β und ∡AD'B=β.
Nach dem Winkelsummensatz im Dreieck ist 7β=180°, also β=1/7·180°.
Die Ecken des 7-Ecks liegen auf dem Umkreis von ABD'.
Mehr:
Das Siebeneck