Die Homepage von Joachim Mohr
Lösung der red. Gl.
Siehe auch Wikipedia
Allgemeine Gleichung 3. Grades
x3+a2x2+a1x+a0=(x-x1)(x2+px+q)
Lösungsformel:
Ich muss zugeben: Die Formel habe ich nicht alleine gefunden, sondern mit Hilfe von
Maple.
Wähle für a=r(sin(φ)+icos(φ)) (r≥0)
_ _ φ φ _
√a=√r(sin(—)+icos(—) mit √r≥0
2 2
— — φ φ —
∛a=∛r(sin(—)+icos(—) mit ∛r≥0
3 3
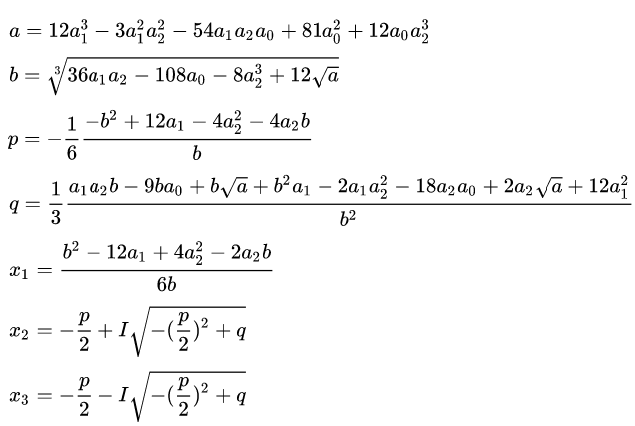
Formel übertragbar
a2=-1
a1=-1
a0=-2
diskriminnte=a2^2*a1^2-4*a1^3-4*a2^3*a0+18*a2*a1*a0-27*a0^2
a=12*a1^3-3*a1^2*a2^2-54*a1*a2*a0+81*a0^2+12*a0*a2^3
b3=(36*a1*a2-108*a0-8*a2^3+12*sqrt(a))
b=b3^(1/3)
p=-1/6*(-b^2+12*a1-4*a2^2-4*a2*b)/b
q=1/3*(a1*a2*b-9*b*a0+b*sqrt(a)+b^2*a1-2*a1*a2^2-18*a2*a0+2*a2*sqrt(a)+12*a1^2)/b^2
x1=1/6*b-6*(1/3*a1-1/9*a2^2)/b-1/3*a2
w=-(p/2)^2+q
x2=-p/2+I*sqrt(w)
x3=-p/2-I*sqrt(w)
probe1=x1^3+a2*x1^2+a1*x1+a0
probe2=x2^3+a2*x2^2+a1*x2+a0
probe3=x3^3+a2*x3^2+a1*x3+a0
Für Maple
restart: a2:=-1; a1:=-1; a0:=-2; pol:=x^3+a2*x^2+a1*x+a0;
a:=12*a1^3-3*a1^2*a2^2-54*a1*a2*a0+81*a0^2+12*a0*a2^3;
b3:=(36*a1*a2-108*a0-8*a2^3+12*sqrt(a)): b:=simplify(b3^(1/3));
diskriminnte=a2^2*a1^2-4*a1^3-4*a2^3*a0+18*a2*a1*a0-27*a0^2;
p:=-1/6*(-b^2+12*a1-4*a2^2-4*a2*b)/b:
q:=1/3*(a1*a2*b-9*b*a0+b*sqrt(a)+b^2*a1-2*a1*a2^2-18*a2*a0+2*a2*sqrt(a)+12*a1^2)/b^2:
x1:=1/6*b-6*(1/3*a1-1/9*a2^2)/b-1/3*a2:
x1r:=simplify(evalc(Re(x1))); x1i:=simplify(evalc(Im(prod))); #Real- und Imaginärteil von x1
w:=-(p/2)^2+q:
x2:=-p/2+I*sqrt(w):
x3:=-p/2-I*sqrt(w):
x1:=simplify(x1); x2:=simplify(x2); x3:=simplify(x3);
probe_pq:=simplify(expand((x-x1)*(x^2+p*x+q)));
probe1:=simplify(x1^3+a2*x1^2+a1*x1+a0);
probe2:=simplify(x2^3+a2*x2^2+a1*x2+a0);
probe3:=simplify(x3^3+a2*x3^2+a1*x3+a0);
probe:=simplify(expand((x-x1)*(x-x2)*(x-x3)));
Beispiele
Die Beispiele wurden berechnet mit TTMathe, was die Rechnungen auf ca 12 Stellen erledigt,
dafür aber einen Formelausdruck wie ∛117+ √227 angibt. Die errechnete Formel wurde anschließend mit Maple überprüft.
x3-3x2-3x-1=0
x1=∛4+∛2+1
p=-(-2^(1/3)-1+2^(2/3))*2^(1/3)
p=∛4+∛2-2;
q=2^(1/3)-1
x2=-1/2*∛4-1/2*∛2+1+1/2*I*sqrt(6*∛2-12+3*∛4))
x3=-1/2*∛4-1/2*∛2+1-1/2*I*sqrt(6*∛2-12+3*∛4))
x^3-x^2-x-2=0
x1=1
x2=-3
x3=3
x^3-x^2+x-1=(x-2)*(x^2+x+1);
x^3+2x^2-x-2=0
a=-108 b=5+sqrt(3) p=3 q=2
x1=1 x2=-2 x3=-1
x^3-x^2+x-1=0
x1=0
x2=I
x3=-I
x^3-x^2+x-1=(x-1)*(x^2+1);
x^3-x^2-x-2=0
x1=2
x2=-1/2+1/2*I*sqrt(3)
x3=-1/2-1/2*I*sqrt(3)
x^3-x^2-x-2=(x-1)*(x^2+6*x+9);
x^3-1/6*x^2+1/12*x-1/8=0
x1=1/2
x2=-1/6+1/3*I*sqrt(2)
x3=-1/6-1/3*I*sqrt(2)
x^3+5*x^2+3*x-9=(x-1/2)*(x^2+1/3*x+1/4);
Die oben agegebene Formel liefert:
x2=1/18*(-z)^(1/3)+I*sqrt(3)*(44+18*sqrt(3)*sqrt(2))^(2/3)+2*I*sqrt(3)/z^(1/3);
mit z=44+18*sqrt(3)*sqrt(2);
x^3+x^2-2*x-8=0
x1=2
x2=1/6*(-z^2-7-2*z+I*sqrt(3)*z^2-7*I*sqrt(3))/z;
x3=1/6*(-z^2-7-2*z-I*sqrt(3)*z^2+7*I*sqrt(3))/z;
für z=(98+21*sqrt(3)*sqrt(7))^(1/3)
Man kann x2 und x3 noch vereinfachen zu:
x2=-3/2+1/2*I*sqrt(7);
x3=-3/2-1/2*I*sqrt(7);
Weitere Beispiele:
a=0
a2=1 a1=-1 a0=-1 ⇒ a=0 b=4 p=2 q=1
x1=1 x2=-1 x3=-1
a2=-5 a1=7 a0=-3 ⇒ a=0 b=4 p=-2 q=1 x1=3 x2=1 x3=1
a2=6 a1=9 a0=4 ⇒ a=0 b=3+3*sqrt(3)i p=5 q=4
x1=-1 x2=-4 x3=-1
a positiv
a2=1 a1=1 a0=1 ⇒ a=48 b=2*sqrt(3)-2 p=0 q=1
x1=-1 x2=i x3=-i
a2=1 a1=-2 a0=-8 ⇒ a=4116 b=sqrt(21)+7 p=3 q=4
x1=2 x2=(-3/2)+1/2*sqrt(7)i x3=(-3/2)-1/2*sqrt(7)i
a2=-1 a1=2 a0=4 ⇒ a=1764 b=5+5*sqrt(3)i p=sqrt(3)*i q=(-1)+sqrt(3)i
x1=1+sqrt(3)i x2=-1 x3=1-sqrt(3)i
a2=1 a1=3 a0=-5 ⇒ a=3072 b=4+4*sqrt(3) p=2 q=5
x1=1 x2=(-1)+2i x3=(-1)-2i
a2=3 a1=1 a0=3 ⇒ a=1200 b=(3-sqrt(3))+(3*sqrt(3)-3)*i p=3-i q=-3*i
x1=-i x2=-3 x3=i
a2=3 a1=2 a0=6 ⇒ a=2904 b=(3-sqrt(6))+(3*sqrt(3)-3*sqrt(2))*i p=3-sqrt(2)i q=-3*sqrt(2)*i
x1=-sqrt(2)*i x2=-3 x3=sqrt(2)*i
a2=3 a1=3 a0=-9 ⇒ a=8100 b=6*100^(1/3) p=10^(1/3)+2 q=1/10*(10*10^(1/3)+10^(2/3)+10)*10^(1/3)
x1=10^(1/3)-1 x2=-1/2*10^(1/3)-1+1/2*I*sqrt(3)*10^(1/3)
x3=-1/2*10^(1/3)-1-1/2*I*sqrt(3)*10^(1/3)
a2=3 a1=5 a0=3 ⇒ a=96 b=2*sqrt(6) p=2 q=3
x1=-1 x2=-1+sqrt(2)i x3=-1-sqrt(2)i
a2=4 a1=2 a0=-7 ⇒ a=1521 b=10 p=5 q=7
x1=1 x2=(-5/2)+1/2*sqrt(3)i x3=(-5/2)-1/2*sqrt(3)i
a2=5 a1=-5 a0=6 ⇒ a=16641 b=8+8*sqrt(3)i p=11/2+1/2*sqrt(3)i q=(-3)+3*sqrt(3)i
x1=1/2+1/2*sqrt(3)i x2=-6 x3=1/2-1/2*sqrt(3)i
a2=-7 a1=17 a0=-20 ⇒ a=2673 b=5+sqrt(33) p=-3 q=5
x1=4 x2=3/2+1/2*sqrt(11)i x3=3/2-1/2*sqrt(11)i
a negativ
a2=1 a1=-2 a0=-2 ⇒ a=-24 b=(1+3*sqrt(2))+(sqrt(6)-sqrt(3))*i p=1+sqrt(2) q=sqrt(2)
x1=sqrt(2) x2=-sqrt(2) x3=-1
a2=-2 a1=-1 a0=2 ⇒ a=-108 b=4+2*sqrt(3)i p=0 q=-1
x1=2 x2=-1 x3=1
a2=-2 a1=-23 a0=4 ⇒ a=-161376 b=(1288+1968*I*sqrt(6))^(1/3) p=1+2*sqrt(2)
x1=2*sqrt(2)+3 x2=-4 x3=3-2*sqrt(2)
a2=3 a1=1 a0=1 ⇒ a=-15 b=(3/2+3/2*sqrt(5))+(3/2*sqrt(3)-1/2*sqrt(15))*i p=1/2*sqrt(5)+5/2 q=1+sqrt(5)
x1=1/2*sqrt(5)-1/2 x2=-2 x3=-1/2-1/2*sqrt(5)
a2=-3 a1=1 a0=1 ⇒ a=-96 b=3*sqrt(2)+sqrt(6)i p=-2+sqrt(2) q=1-sqrt(2)
x1=1+sqrt(2) x2=1-sqrt(2) x3=1
a2=3 a1=-1 a0=-6 ⇒ a=-39 b=(3/2+3/2*sqrt(13))+(1/2*sqrt(39)-3/2*sqrt(3))*i p=1/2*sqrt(13)+5/2 q=1+sqrt(13)
x1=1/2*sqrt(13)-1/2 x2=-1/2-1/2*sqrt(13) x3=-2
a2=4 a1=1 a0=-6 ⇒ a=-432 b=7+sqrt(3)i p=5 q=6
x1=1 x2=-3 x3=-2
a2=4 a1=2 a0=-4 ⇒ a=-144 b=(1+3*sqrt(3))+(3-sqrt(3))*i p=sqrt(3)+3 q=2+2*sqrt(3)
x1=sqrt(3)-1 x2=-1-sqrt(3) x3=-2
a2=4 a1=3 a0=-2 ⇒ a=-24 b=(1+3*sqrt(2))+(sqrt(6)-sqrt(3))*i p=sqrt(2)+3 q=2+2*sqrt(2)
x1=sqrt(2)-1 x2=-1-sqrt(2) x3=-2
a2=4 a1=3 a0=-8 ⇒ a=4116 b=sqrt(21)+7 p=5 q=8
x1=1 x2=(-5/2)+1/2*sqrt(7)i x3=(-5/2)-1/2*sqrt(7)i
a2=5 a1=3 a0=-1 ⇒ a=-960 b=(3*sqrt(5)-1)+(sqrt(3)+sqrt(15))*i p=sqrt(5)+3 q=2+sqrt(5)
x1=sqrt(5)-2 x2=-2-sqrt(5) x3=-1
a2=5 a1=-5 a0=-1 ⇒ a=-6144 b=8+4*sqrt(6)i p=6 q=1
x1=1 x2=-2*sqrt(2)-3 x3=-3+2*sqrt(2)
a2=-5 a1=7 a0=-2 ⇒ a=-15 b=(3/2*sqrt(5)-1/2)+(1/2*sqrt(3)+1/2*sqrt(15))*i p=-7/2+1/2*sqrt(5) q=3-sqrt(5)
x1=1/2*sqrt(5)+3/2 x2=3/2-1/2*sqrt(5) x3=2
a2=-5 a1=7 a0=-3 ⇒ a=0 b=4 p=-2 q=1
x1=3 x2=1 x3=1
a2=5 a1=-7 a0=1 ⇒ a=-4320 b=8+2*sqrt(30)i p=6 q=-1
x1=1 x2=-3-sqrt(10) x3=sqrt(10)-3
a2=-6 a1=1 a0=4 ⇒ a=-7872 b=(1080+96*I*sqrt(123))^(1/3) p=-7/2+1/2*sqrt(41) q=-1/2*sqrt(41)+5/2
x1=5/2+1/2*sqrt(41) x2=-1/2*sqrt(41)+5/2 x3=1