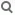Die Homepage von Joachim Mohr
Wie löse ich die Gleichung x·ex=a nach x auf?
 Die Gleichung x·ex=a läßt sich elementar nicht nach x
auflösen.
Die Gleichung x·ex=a läßt sich elementar nicht nach x
auflösen.Du musst dazu ein numerisches Verfahren (zum Beispiel das Newton- oder Intervallhalbierungsverfahren) verwenden.
Da die Gleichung jedoch immer wieder mal auftaucht, gibt es Tabellen für die Lösung: die sogenannte Lambert'sche W-Funktion. (Manche Computerprogramme, zum Beispiel TTMathe haben diese Funktion integriert.)
Beachte jedoch, dass es für -1/e < a < 0 zwei Lösungen gibt.
Beispiele:
a) x·ex=2,2 => x=0,897
b) x·ex=-0,1
=> x1=-0,112 und x2=-3,577
a) x·ex=2,2 => x=0,897
b) x·ex=-0,1
=> x1=-0,112 und x2=-3,577
Hinweis für Programmierer: Um die Umkehrfunktion zu bestimmen, kann man für jeden y-Wert die Nullstelle der Hilfsfunktion h(x) = x·ex - y berechnen. Für y > 0 ist das Newtonverfahren das geeignete, für y kleiner 0 nicht, da die Funktion h bei -1 eine waagrechte Tangente hat. Mit dem Intervallhalbierungsverfahren ist die Ermittlung der Nullstelle von h jedoch kein Problem. Für den Hauptwert lam(y) beginnt man mit dem Intervall (-1,0) für den Nebenwert Lam(y) mit dem Intervall (x,-1), wobei x kleiner -1 so "eingefädelt" wird, dass h(x) positiv ist, da h(-1) negativ ist.
Viele andere Gleichungen lassen sich auf diese Fragestellung zurückführen:
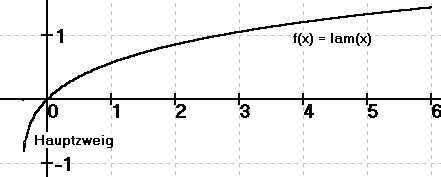
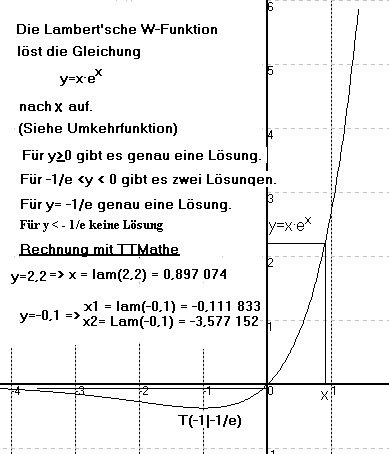
Dazu muss man beachten x·ex = a => x = lam(a).
Für -1/e kleiner a kleiner 0 gibt es noch die 2. Lösung x = Lam(a)
Die Lambertsche W-Funktion
y=lam(x) Hauptzweig der Lambertsche W-Funktiony=Lam(x) Nebenzweig der Lambertsche W-Funktion
Mehr zur Lambert'schen W-Funktion siehe MathWorld
Beispiel 1:
x
- x
3 1 - -
3·e = - -x 3
e => x·e = -3e
x z
Substitution z = - - führt auf die Gleichung: z·e = e
3
Die Lösung ist z = lam(e)=1 und somit x = - 3·lam(e) = -3
Beispiel 2:
x
x·b = a (a>0, b>0)
Lösung:
x xlnb xlnb
Mit b = e lautet die Gleichung x·e = a
z z
Substitution z=xlnb führt auf ———·e = a
lnb
z
Fertig! z·e = a·lnb
Die Lösung lautet: z = lam(a·lnb)
(Für a>0,b>0 genau eine Lösung)
Rücksubstition: xlnb = lam(a·lnb)
lam(a·lnb)
Ergebnis: x = ——————————
lnb
x
Zum Beispiel: x·2 = 10 hat die
lam(10ln2)
Lösung x = —————————— = 2,190 601 218
ln2
Beispiel 3:
x + lnx = a
Lösung:
x + lnx a u + v e v lnx
e = e . Mit e = e ·e und e = x folgt:
x a a
x·e = e . Lösung: x = lam(e )
Zum Beispiel:
2
x + lnx = 2 hat die Lösung x = lam(e ) = 1,557 146
Beispiel 4:
a·x + b·lnx = c
a c
-x + lnx -
a c b b
Lösung: -x + lnx = - => e = e =>
b b
a c
-x -
b b a
x·e = e Substitution: z = -x
b
c c
- -
b z b z a b
-z·e = e => z·e = -·e . Fertig!
a b
c
-
a b
z = lam( -· e ) und somit:
b
c
-
b a b
x=-·lam(-·e )
a b
Zum Beispiel:
1 3
2x+lnx=3 hat die Lösung: x = -lam(2e ) = 1,349 962
2
Der Geübte rechnet:
2x 3 3
2x+lnx=3 => 2x·e = 2e => 2x=lam(2e ) Fertig!
Beispiel 5:
ax + q· log x = c, wobei log der
p p
Logarithmus zur Basis p sei.
lnx q
Mit log x = ——— und b = ——— kann man
p lnp lnp
wie in Beispiel 4 rechnen.
Beispiel 6:
x a
a = x hat die Lösung x = a und
a lna
x = - ———lam(- ———) für x,a > 0.
lna a
x a
Herleitung: a = x => xlna - alnx = 0.
Nun kann man wie in Beispiel 4 rechnen:
lna
- ———x
lna a
- ———x - lnx =0 => xe = 1.
a
lna a
Substitution z = - ———x oder x = - ———z ergibt:
a lna
z lna lna a lna
ze = - ——— . Somit z = lam(- ———) und x = - ———lam(- ———)
a a lna a
lna
I Genau eine Lösung, wenn - ——— ≥ 0 , d.h. 0 kleiner a ≤ 1.
a
1 lna
II Genau zwei Lösungen, wenn - - kleiner - ——— kleiner 0. d.h. a größer 1.
e a
lna 1
III Grenzfall: Genau eine Lösung, wenn - ——— = - -,
a e
also a = e.
lna
Hilfsmittel: Das Schaubild von a -> ——— hat
a
1
den Hochpunkt H(e|-).
e
Zusammenfassung
x a
a = x hat für 0 kleiner a ≤ 1 und a = e die
triviale Lösung x = a.
Für a > 1 und a ≠ e gibt es außer der
trivialen Lösung x=a noch eine zweite
a lna
Lösung x = - ———lam(- ———).
lna a
Diese Werte lassen sich nur näherungsweise
berechnen.
Hochinteressant sind die beiden Zweige
a lna
x1 = - ———lam(- ———) und
lna a
a lna
x2 = - ———Lam(- ———).
lna a
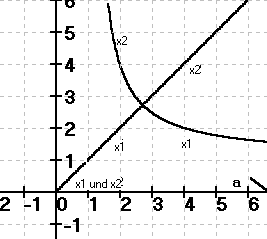
Siehe dazu auch die folgende Fragestellung?
Wann hat die Gleichung xy = yx eine weitere Lösung außer x=y?
Beispiel 7:
y
Die Gleichung y=a·x·ln(b·x) hat die Lösung x = —————————
y
a*lam(——)
ba
y y
Herleitung: y=ax·ln(bx) => —— = ln(bx) => exp(——) = bx
ax ax
y y by
Substitution z = —— , x = —— ergibt: exp(z) = ——
ax az az
by
Daraus folgt: z·exp(z) = ——.
a
Also mit der Lambert'schen W-Funktion:
y y y
z = lam(——) Mit x= —— folgt: x = ——————————
ba az by
a·lam(——)
a
Beispiel 8: Die Gleichung xx = a kann durch x·ln(x)=ln(a) auf Beipiel 7
zurückgeführt werden:Lösung:
ln(a)
x= ——————————
lam(ln(a))
Für a=7 ist zum Beispiel mit x=2,316 454 958 785 612 3
2,3164549587856123
2,3164549587856123 = 7
Wann hat die Gleichung xy = yx eine weitere Lösung außer x=y?
Anwort: Wir setzen im Folgenden x > 0 und y > 0 voraus.
y x lnx lny
x = y äqivalent ylnx = xlny äquivalent ——— = ———
x y
lnx
Betrachten wir nun die Funktion f(x) = ———.
x
Dann lautet unsere Frage: Wann ist f(x) = f(y) für x ≠ y ?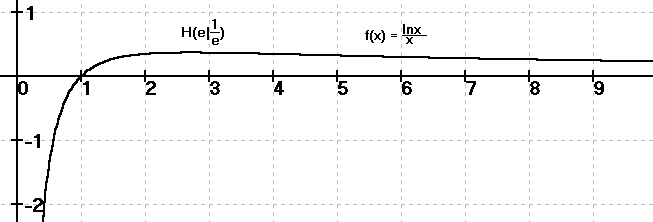
Zu untersuchen ist also: Wann ist f nicht injektiv (nicht eineindeutig)?
Am besten sieht man das am Schaubild: Für x > 1 gibt es außer für x ≠ e noch eine zweite Lösung der Gleichung f(x) = f(y).
ln2 ln4 4 2
Zum Beispiel f(2) = f(4), d.h. ——— = ——— also 2 = 4 oder
2 4
ln1,371288575 ln10
f(1,371288575) = f(10), d.h. ————————————— = ————
1,371288575 10
10 1,371288575
also 1,371288575 = 10 .
Siehe dazu auch das Beispiel 6 zu der Lambertschen Funktion
Was ist hier faul?
—— —— ————————— -
-1 = \/-1·\/-1 = \/(-1)·(-1) = \/1 = 1
Bei den "komlexen Zahlen" handelt es sich um einen Zahlenbereich, der die reellen Zahlen
umfaßt, bei dem es aber noch eine weitere Zahl i gibt mit i2 = -1. Diese Zahl wird
fälschlicherweise häufig mit "Wurzel von -1" bezeichnet.Das Falsche daran ist, dass "Wurzel von -1" als Lösung der Gleichung x2= -1 nicht eindeutig ist. Im reellen Zahlenbereich hat die Gleichung keine Lösung, im komplexen Zahlenbereich jedoch zwei Lösungen.
Antwort: Das Problem ist hier, dass Du eine für reelle Zahlen>=0 gültige Regel
- - ———
\/a·\/b = \/a·b (Produktregel)
ohne Bedenken auch fuer andere Werte verwendest. Es gibt keine Funktion
—— -2 "\/ " mit der Eigenschaft \/x = xfür Werte ausserhalb der reellen Zahlen ≤ 0, die die obigen Eigenschaft hat. Man könnte zwar willkürlich
——
\/-1 := i
definieren, aber dann darf man die obige Produktregel nicht anwenden, weil sie halt nicht gilt.Nochmal das Fazit: Es gibt keine eindeutig definierte Wurzelfunktion für Werte ausserhalb der Zahlen ≥ 0, für die die Produktregel gilt.(Horst Kraemer).
- Manchmal spricht man vom Hauptwert √a der Quadratwurzel aus a ε C. Es ist aber davor zu
warnen, das Wurzelzeichen gedankenlos zu verwenden.
Noch ein Beispiel gedankenloses Rechnens:
—— -
—— \/-1 \/1 1
i = \/-1 = ———— = ———— = - = - i => i = 0 (falsch!!!)
- —— i
\/1 \/-1
Frage:
Ich schreibe gerade an einem Programm zur ganzzahligen Optimierung. Dabei rufe ich ein externes Programm auf, das mir einfache Brüche als Dezimalzahlen zurückliefert. Zum Beispiel: statt 4/3 wird 1.333...33 geliefert.
Das Dumme: Mein Computer kann ja nicht "sehen", dass 1.333...33 ein einfacher Bruch ist. Gibts für solche Probleme einen Algorithmus, der das dann auf ganzzahlige Koeffizienten bis auf eine gewisse Ungenauigkeit annähert?
Antwort: Ja. Das Stichwort dazu heißt Kettenbruch. Dort ist auch ein Algorithmus dazu aufgeführt (Euklidischer Algorithmus). Diesen Algorithmus findest Du umgesetzt in Delphi als Funktion Reell Zu Bruch