Joachim Mohr Mathematik Musik
Lektionen der Analysis in Aufgaben
 |
Lektionen der Analysis in Aufgaben Lösungen |
|
1. Lektion: Geraden in der x-y-Ebene
siehe dazu auch Punktsteigungsform und Zweipunkteform
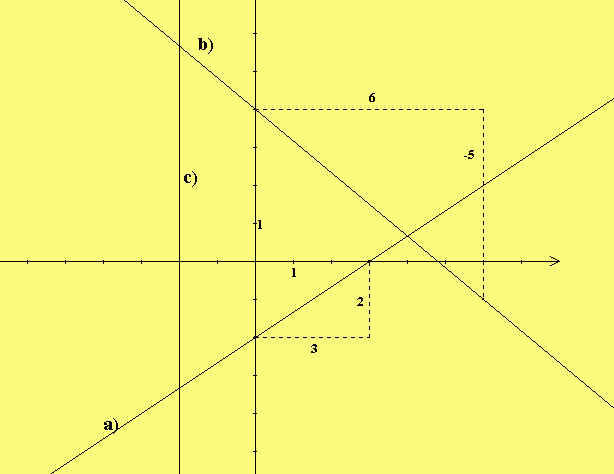
1. Gib die Gleichungen der Geraden an und prüfe,
ob der Punkt X auf ihr liegt.
Lösung:
y - y
2 1
Berechne zuerst die Steigung m = —————— (falls x2 ≠ x1)
x - x
2 1
der Geraden durch P(x |y ) und Q(x |y )
1 1 2 2
und berechne aus y = mx + c den y-Abschnitt c
durch Punktprobe oder rechne gleich mit der
Punktsteigungsform: y= m(x-x ) + y
1 1
(Gerade durch P(x |y ) mit der Steigung m)
1 1
1
a) Die Gerade durch P(6|0) Q(0|3): y = - -x + 3.
2
X(10|-2) liegt auf der Geraden.
b) Die Gerade durch A(2|2) parallel zur Geraden durch B(0|-1) C(1|1):
y = 2x - 2. X(10|20) liegt nicht auf der Geraden, sondern Y(10|18).
c) Die Gerade durch Q(0|3) parallel zur x -Achse: y = 3.
d.h. Alle Punkt X(x|y) mit (x beliebig und) y = 3 liegen auf der Geraden.
X(11|3) liegt auf der Geraden.
d) Die Gerade durch N(3|0) parallel zur y -Achse: x = 3
d.h. Alle Punkt X(x|y) mit (y beliebig und) x = 3 liegen auf der Geraden.
X(3|11) liegt auf der geraden.
Δy
2. Zeichne bei a) und b) ein Steigungsdreieck aus m = ——
Δx
10. Lektion: Produkt-, Quotienten- und Kettenregel
Siehe auch: "Kettenregel"!
2
2 2t 2 3
1 a) f(x) = 2x ·sinx b) g(t) = ———— c) h(x) = (4 - 5x )
sint
Lösungen:
2
a) f'(x) = 4x·sinx + 2x cosx
2
4t·sint - 2t cost
b) g'(t) = —————————————————
2
sin t
2 2
c) h'(x) = - 30x(4 - 5x )
2 2
2 2a t 2 3 2 3
2 a) f (x) = 2t xsinx b) g (t) = ————————— c) h (x) = (t - t x )
t a (a-1)cost t
Lösungen:
2 2
a) f' (x) = 2t sinx + 2t xcosx
t
2 2 2 2 2
4(a-1)a tcost + 2(a-1)a t sint 2a (2tcost + t sint)
b) g'(t) = —————————————————————————————— = ————————————————————
a 2 2 2
(a-1) cos t (a-1)cos t
3 2 3 2 2
c) h'(x) = - 6t x(t - t x )
t
1 2
- -x
—————— -kt 2
3. a) f(x) = \/2 - 4x b) g(t) = G - ae c) h(x) = (x-1)e
Lösungen:
2
a) f'(x) = - ————————
——————
\/2 - 4x
-kt
b) g'(t) = ake
1 2
- -x
2 2
c) h'(x) = (- x + x + 1)e
11. Lektion: Erst umformen, dann ableiten
Forme erst um und leite dann ab!
Aufabe und Lösung:
3 2
t(x - 2x + 3) 3 6
a) f (x) = ————————————— = t(x - 2 + ——) => f'(x) = t(1 - ——)
t 2 2 t 3
x x x
5 -2 20
b) f(x) = ————————— = 5(2x-1) => f'(x) = - ———————
2 3
(2x - 1) (2x-1)
12. Lektion: Stammfunktionen und Integrale
Ermittle die Stammfunktion! Mache stets die Probe durch Ableiten!
5 1 -4t
1. a) f(x) = 5(2x - 4) b) g(t) = -cos2t c) h(t) = 10 - 3e
2
Lösung:
5 6 5 5
a) F(x) = ——(2x - 4) F'(x) = ——·6·2(2x-4) = f(x)
12 12
1 1
b) G(t) = -sin2t G'(t) = -·(cos2t)·2 = g(t)
4 4
3 -4t 3 -4t
c) H(t) = 10t + -e H'(t) = 10 + -·(-4)e = h(t)
4 4
2 5 2 -kt
2. a) f (x) = t(tx - t ) b) g (t) = asina t d) h(t) = G - ae
t a
Lösung:
1 2 6 1 2 5
a) F (x) = -(tx - t ) F'(x) = -·6(tx - t ) ·t = f (x)
t 6 t 6 t
1 2 1 2 2
b) G (t) = - -cosa t G'(t) = - -(-sina t)·a = g (t)
a a a a a
a -kt a -kt
c) H(t) = Gt + -e H'(t) = G + -·(-k)e = h(t)
k k
3. Aufgaben und Lösungen:
2π 2π
x x π
a) I sin-dx = [- 4cos-] = - 4cos- + 4cos0 = 4
4 4 2
0 0
3
8 - 8 8
—— 1 2 1 —— 64
b) I\/2xdx = [-(2x) ] = {-2x\/2x)] = ——
3 2 3
0 0 0
∞ ∞
1 1 1
c) I ———————dx = lim [- ———————] = -
2 2(2x+2) 4
0 (2x+2) u->∞ 0
4. Aufgaben und Lösungen
1 1 1
x - -t - -t x - -x
2 2 2
a) I e dt = [ - 2e ] = 2 - 2e
0 0
x x
π 2 π 2 π
b) I sin-tdt = [ - -cos-t] = -(1 - cos-x)
2 π 2 π 2
0 0
x x
1 1
c) I f'(2t)dt = [-f(2t)] = -(f(2x) - f(0)]
2 2
0 0
20. Lektion: Asymptoten
2 2
2x - 3 x - 2x + 1 x - 2x + 1
1 a) f(x) = —————— b) f(x) = —————————— c) f(x) = ———————————
3 - 4x 2x 2x - 1
Lösungen:
3
a) Pol (senkrechte Asymptote) x = -
4
1
Verhalten für x -> ±∞ (waagrechte Asymptote) y = - -
2
b) Pol (senkrechte Asymptote) x = 0 (y-Achse)
1 1 1
Verhalten für x -> ±∞ (schief Asymptote) y = -x - 1, da f(x) = -x - 1 + ——
2 2 2x
1 1
und lim f(x) - (-x - 1) = lim —— = 0
x->∞ 2 2x
x->∞
1 3 1
c) Polynomdivision ergibt f(x) = -x - - + ———————
2 4 4(2x-1)
1 1 3
Pol x = - schiefe Asymptote y = -x - - (siehe auch Koefizientenvergleich)
2 2 4
1
x - -x
-0.001t e + 3 2
2 a) f(t) = 2 - e b) f(x) = —————— c) f(x) = (1 - 4x)e
x
2 - e
Lösungen:
a) Asymptote ist die (positive) x-Achse, da lim f(t) = 0
x->∞
b) senkrechte Asymptote (Pol) x = ln2
waagrechte Asymptote (Verhalten für x->+∞) y = -1
3
waagrechte Asymptote (Verhalten für x->-∞) y = -
2
c) waagrechte Asymptote (Verhalten für x->+∞) y = 0
kx kx 2 kx
Beachte: lim e = 0, lim xe = 0, lim x e = 0, ... (k < 0)
x->∞ x->∞ x->∞
kx kx 2 kx
lim e = 0, lim xe = 0, lim x e = 0, ... (k > 0)
x->-∞ x->-∞ x->-∞
21. Lektion: Symmetrien
Siehe Beispiele im Kapitel "Symmetrien"22. Lektion: Tangenten und Normalen
1. a) Bestimme die Gleichung der Tangente und Normalen an das
1 4 2
Schaubild der Funktion f mit f(x) = -x - 2x - x + 1 im Punkt P(1|?)
8
und berechne deren Schnittpunkte mit den Achsen.
1 3 15 9 15 9
Lösung: f'(x) = -x - 4x - 1; f(1) = - —— f'(1) = - - => P(1|- ——; - -)
2 8 2 8 2
1 2 1
b) Dasselbe für f(x)=-(x+1) - - im Punkt P(2|?)
4 4
1 3 3 3
Lösung: f'(x) = -(x-2) + - = -x - 1 P(2|2;-)
2 2 2 2
3 2
Tangente y = -x - 1 Achsenabschnitte A(0|-1) B(0|-)
2 3
Allgemein: Die Gerade durch P(x0|y0) mit der Steigung m=f'(x0) lautet:
y=m·(x-x0)+y0 Probe: für x=x0 erhält man y=y0
y=m·(x-x0)+y0 Probe: für x=x0 erhält man y=y0
9 21 7 21
Tangente: y = - -x + —— Achsenschnittpunkte N(——|0) Q(0|——)
2 8 12 8
2 151 151 151
Normale: y = -x + ——— Achsenschnittpunkte N(———|0) Q(0|———)
9 72 16 72
-x
2. A(u|v) mit u>0 sei ein Punkt des Schaubildes K von f(x) = e . Die
Parallele durch A zur x-Achse schneide die y-Achse in B. Die Tangente
in A an das Schaubild K schneide die y-Achse in C. Für welchen Wert
von u wird der Flächeninhalt des Dreiecks extremal?
-u -u -u -u -u
Lösung: Tangente in A(u|e ); - e ): y = -e x + ue + e
-u -u 1 -u
=> C(0|ue + e ). Flächeninhalt des Dreiecks ABC: A(u) = -u(2-u)e .
2
Um das Extremum zu bestimmen setzten wir A'(u) = 0:
1 -u
A'(u) = -u(2 - u)e = 0 bei u = 2 mit Vorzeichenwechsel von A' vom "+"
2
-2
nach "-". => Relatives Maximum A(2) = 2e .
Da die Randwerte lim A(0) = 0 und lim A(u) = 0 handelt es sich
u->0 u->∞
um ein absolutes Maximum.
3. Vom Punkt P(3|0) sollen die Tangenten an das Schaubild der Funktion f
2
mit f(x) = - + 2 gelegt werden.
x
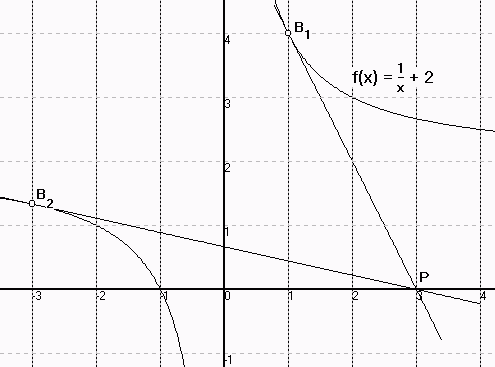Lösung: Sei B(u|f(u)) ein Berührpunkt.
Die Gleichung der Tangente in B ist dann y = f'(u)(x - u) + f(u)
2 2
Hier: f(x) = - + 2 => f'(x) = - ——
x 2
x
2 2
Tangente in B: y = - - (x - u) + - + 2 (*)
2 u
u
Die Tangente soll durch P(3|0) gehen. Mache also in (*) die "Punktprobe"
2 2
mit x = 3 und y = 0. Man erhält die Gleichung - - (3 - u) + - + 2 = 0
2 u
u
2 2
Mit u durchmultipliziert ergibt sich -2(3 - u) + 2u + 2u = 0.
2
Zu lösen ist also die quadratische Gleichung u +2u - 3 = 0
4
mit den Lösungen u = 1 und u = -3 mit den Berührpunkten B (1|3) und B (-3|-).
1 2 1 2 3
Man kann also von P(3|0) zwei Tangenten an das Schaubild von f legen.
Ihre Gleichungen sind dann y = -2x + 6 mit Berührpunkt B (1|3) und
1
2 4 4
y = - -x + - mit Berührpunkt B (-3|-).
9 3 2 3
23. Lektion: Verschiebung von Schaubildern
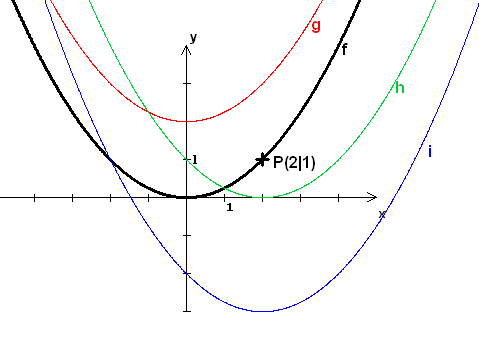a) Bestimme die Gleichung y=f(x) der Parabel durch den Ursprung O(0|0) und P(2|1), die symmetrisch zur y-Achse ist.
b) Die Parabel von Teil a) wird um +2 in Richtung y-Achse verschoben. Bestimme die Gleichung y=g(x).
b) Die Parabel von Teil a) wird um +2 in Richtung y-Achse verschoben. Bestimme die Gleichung y=g(x).
c) Die Parabel von Teil a) wird um +2 in Richtung x-Achse verschoben. Bestimme die Gleichung y=h(x).
d) Die Parabel von Teil a) wird um -3 in Richtung y-Achse und um +2 in Richtung x-Achse verschoben. Bestimme die Gleichung y=i(x).
Lösung:
a) Ist das Schaubild von f eine Parabel, dann ist f von der Form: f(x)=ax2 + bx + c
Hier, wegen der Symmetrie zur y-Achse: f(x)=ax2 + c.
Da die Parabel durch den Ursprung geht, ist f(0)=0, also c=0.
Punktprobe bei f(x)=ax2 mit dem Punkt P(2|1) ergibt 1=a·22, also a = 1/4
1 2
Somit: f(x) = -x
4
1 2
b) g(x) = -x + 2 (Im Vergleich zu a) muss zu jedem y-Wert muß 2 addiert)
4
1 2
c) h(x) = -(x-2)
4
1 2 1 2
Probe: h(1)= -(1-2) = -(-1) = f(-1)
4 4
1 2
h(2) = -(2-2) = f(0)
4
1 2
h(3) = -(3-2) = f(1)
4
u.s.w.
Man sieht. Bei Punkten vom Schaubild von h muss man x um 2 erhöhen, um denselben y-Wert wie beim
Schaubild von f zu erhalten.
Merke: verschiebt man das Schaubild von f um a nach rechts, so erhält man das Schaubild von h
mit h(x) = f(x-a).
1 2 1 2
d) i(x) = -(x-2) - 3 = -x - x + 1
4 4
24. Lektion: Exponentialfunktion und Logarithmus
1. 2x 2x
1 -1/3x 1 2x 2x 2x 2e (2e + 1)
a) f'(x) = - - e b) g'(x) = -e + (x+2)e = (x+2,5)e c) h'(x) = ———————————————
3 2 2x 2
(e + 1)
a ln(b) x
2. Merke ln(e ) = a. Umgekehrt: e = b, da y=e ⇔ x = ln(y)
a log(b) 4 log(100)
Mit dem Zehnerlogarithmus: log(10 ) = a, 10 = b. Beispiel: log(10 ) = 4, 10 = 100.
1 1 - 1
a) -x b) -x c) \/x d) - + x Beachte ln(a•b) = ln(a) + ln(b)
2 2 x
3) Punkte des Schaubildes sins
a) A(-5|0,4) B(0|1) C(5|2,7) b) a(-5|2,7) B(0|1) C(5|0,4) c) A(-5|-4,6) B(0|1) C(5|5,4)
-1/2x -1/2x -1/2x a
4. f(x) ≥ g(x) = x + e > x + e ⇔ 2e > 0, da stets: e > 0
a -1/2x -1/2x a -1/2a
b) I = lim ∫ 2e dx = lim [-4e ] = lim (-4e + 4) = 4
a → oo 0 a → oo 0 a → oo
kx kx
5. Du musst wiseen: f(x) = Ae ⇒ f'(x) = kAe = k•f(x) und f(0) = A
2/3x
Somit lautet unsere Funktion f(x) = 200•e
25. Lektion: Vermischte Aufgaben
A1 a)Eine ganzrationalen Funktion 3.Grades, symmetrisch zum Ursprung ist von der Form
f(x)=ax3+bx ⇒ f'(x)=3ax2+b
Tiefpunkt für x=√3 ⇒f'(√3)=0 ⇒ 9a+b=0 ⇒ b=-9a
f(x)=ax3-9ax=ax(x2-9)
Aus f(√3)=-2√3 folgt: a√3(3-9)=-2√3 ⇒ a=1/3 und b=-3 somit
f(x)=1/3x3 - 3x, f'(x) = x2 - 3, f''(x)=2x
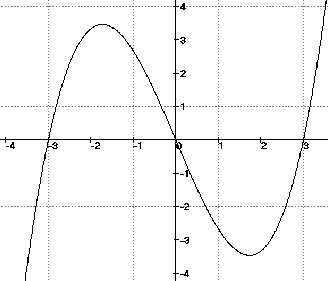
b)
f'(0) = -3 ⇒ An der Stelle x=0 ist die Funktion streng monoton fallend.
Ein Vorzeichenwechsel von f' von "-" nach "+" an der Stelle x0 bedeutet:
Vor x0 "monoton fallend" und nach x0 "monoton steigend".
Graph ca. \ /
—
Also befindet sich bei x0 ein Minimum.
Die Funktionen f(x)=x2, g(x)=x4 haben bei x=0 einen Tiefpunkt. f''(0)=2 aber g''(0)=0.
c)
y
\ ↑ /
\ | /
ungefähr so: \ | /
\| /
———————————→ x
|
Schaubild hat bei x=0 einen "Knick", keine Tangente, die Funktion ist dort nicht differenzierbar,
hat aber dort ein Minimum.
A2 bi sA8 Löungen noch nicht eingestellt.
30. Lektion: Lineares Wachstum
Aufgabe: Lena hat einen Smartphonevertrag (mit einer Telefonflatrate) mit einem monatlichen Basistarif. Jede Minute, die sie im Internet ist, wird jedoch abgerechnet. Im ersten Monat bezahlt Sie für 6 Stunden online 18 € im zweiten Monat für 11 Stunden online 22 €. Im dritten Monat ist sie 15 Stunden online. Wie hoch sind dann die Kosten.Lösung:
Eine Wachstumsfunktion ist von der Form
f(x) = m·x + c (Hier: x Minuten online, f(x) Preis in Euro)
Bekannt: f(360) = m·360 + c = 18 (1)
f(660) = m·660 + c = 22 (2)
————————————————————————————————————
m·300 = 4 (2) - (1)
=> m= 1/75 c=14
1 66
Somit: f(x) = ——x + ——
75 5
f(900) = 25,2
Ergebnis: Im 3. Monat betragen die Kosten 25,2 €.
31. Lektion: Exponentielles Wachstum
Das solltest Du wissen:
Exponentielles Wachstum:
kx
Funktion: f(x) = A·e mit A = f(0)
Differentialgleichung: f'(x) = k·f(x)
Die momentane Änderungsrate ist proportional zum Bestand
1.Aufgabe:
Borgland hatte im Jahr 2018 eine Verschuldung von 60% seines Bruttoinlandsprodukts. Seine Verschuldung wächst jährlich um 11 %. Spätestens bei einer Verschuldung von 150% erklären die Ratingagenturen, dass der Staat die Schulden nicht mehr zurückzahlen kann. Dann gewährt niemand mehr Kredit. Der Staat ist dann bankrott. In welchem Jahr dürfte dieses Ereignis eintreten?
kx
Ansatz: f(x) = A·e (x vergangene Jahre seit 2008;
f(x) Verschuldung in Prozent seines Bruttoinlandsprodukts).
Aus f(0) = 60 folgt A = 60.
Nach einem Jahr hat die Verschuldung um 11% zugenommen, d.h.
k 11
f(1) = A·e = A + ———A = A·1,11 => k = 0,1044 (Empfehlung: 4 "geltende Ziffern")
100
0,1044x
Somit: f(x) = 60·e
Der Schuldenstand von Borgland ist im Jahre x auf 150 % gestiegen:
0,1044x 0,1044x
60·e = 150 => e = 2,5 => 0,1044x = ln 2,5 => x = 8,8 Jahre.
Ergebnis: Borland wird nach dieser Modellrechnung im Jahre 2027 seinen Bankrott erkären.
2. Aufgabe
Die Frequenzen von Vielfachen eines musikalischen Intervalls wachsen exponentiell:
Intervall Frequenzverhältnis
1 Oktave 2
2 Oktaven 4
3 Oktaven 8
4 Oktaven 16
...
n
n Oktaven 2
Intervalle werden in ihrer Größe als Vielfache von einem Cent angegeben, wobei 1200 Cent = 1 Oktave.
Berechne die Größe einer Quinte in Cent!
Hinweis: Berechne das passende n für Quinte = n·Oktave = 1200·n·Cent mit Hilfe des Frequenzverhältnisses q=3/2 der Quinte.
Lösung:
Es ist die Gleichung 2n = p = 3/2 zu lösen:
n
2 = q <=&tt; n = 2log(q)
Also: Quinte = 1200 · 2log(3/2) Cent = 702 Cent
log(q)
Bemerkung: Mit dem Taschenrechner: log(q) = —————— (Logarithmus zur Basis 2)
2 log(2)
32. Lektion: Beschränktes Wachstum
Das solltest Du Dir merken!
-kx
Funktion: f(x) = S - c·e mit f(0) = S - c (*)
Differentialgleichung: f'(x) = k·(S - f(x)) (**)
Die momentane Änderungsrate ist proportional zum "Sättigungsmanko"
(das was bis zur Schranke S noch fehlt).
a) f'(x) = 0,1·(100 - f(x)) mit f(0) = 20 b) f'(t) = 20 - 0,3·f(t) mit f(0) = 30Lösung zu a) Man kann nach (*)und (**) sofort ablesen k = 0,1 und S= 100. Somit
-0,1x
f(x) = 100 - c·e . Mit f(0) = 100 - c = 20 folgt c = 80
Lösung zu b) Hier müssen wir die Differenzialgleichung erst umformen.
20
f'(t) = 0,3·——— - 0,3·f(t) = 0,3·(66,67 - 0,3·f(t))
0.3
Wieder ist sofort ablesbar: k = 0,3 und S = 66,67.
-0,3t
Somit ist f(t) 66,67 - c·e . Mit f(0)=20 folgt c= 46,67
2. Aufgabe: Wird Salz in Wasser gelöst, ist dies bei einer bestimmten
Temperatur nur bis zu einer bestimmten Sättigung möglich. Die Geschwindigkeit wie sich
das Salz löst, ist proportional zur Restmenge des noch lösbaren Salzes.
a)Bestimmen Sie die Funktion t-> m(t) (t: Zeit in Stunden, m(t) = Prozent der maximal lösbaren Salzmenge) bei einem Proportionalitätsfaktor von k = 3.
b) Wann sind 50% der Sättigung erreicht, falls am Anfang noch kein Salz gelöst ist.
-kt
Ansatz: m(t) = S - c·e
m'(t) = 3·(100 - m(t))
Also ist S= 100 und k = 3.
-3t
m(t) = 100 - c·e .
Setzt man noch m(0) = 0 voraus:
-3t
m(t) = 100 - 100·e
-3t
b) m(t) = 100 - 100·e = 50
-3t -3t
=> 100·e = 50, e = 0,5, -3t = ln0,5, also t=0,231 Stunden ~ 14 Minuten
3. Aufgabe:
In einer Stadt gibt es 40000 Haushalte, von denen schätzungsweise jeder
fünfte für den Kauf eines neu auf den Markt gebrachten Haushaltsartikels
in Frage kommt. Es ist damit zu rechnen, dass der Absatz des Artikels im
Laufe der Zeit schwieriger wird, da der Kreis der Käufer und deren Kauflust
abnimmt. In den ersten drei Monaten werden 1700 Stück des Artikels verkauft.
Kann der Hersteller davon ausgehen, dass innerhalb des ersten Jahres wenigstens 5500 Stück verkauft werden?
Lösung: Sättigungsgrenze S=8000
-kt
f(t)=8000-8000·e
-3k
f(3)=8000(1-e )=17000 => k=0,07963
Verkauf nach einem Jahr: f(12) = 4923. Hoffnung des Händlers zu optimistisch.
4. Aufgabe:
Pegelstand in einem Wasserreservoir:
t->V(t) Volumen des Wassers (t in Minuten, V(t) in Kubikmeter)
bekannt: V(0)=20
3
Zufluss: 0,15 m pro Minute
Abfluss: 0,25% des Inhalts pro Minute.
Bestimme die Funktion t -> V(t)
Lösung:V'(t)=0,15-0,0025·V(t)
Das ist die DGL des beschränkte Wachstums,
Umformung ergibt: v'(t) = 0,0025·(60 - V(t)
-0,0025·t
Also ist: V(t)=60-a·e
-0,0025·t
Mit V(0)=20 ergibt sich V(t)=60-40·e
33. Lektion: Logistisches Wachstum
Das solltest Du Dir merken!
S
Funktion: f(x) = —————————— (*)
-kx
1 + a·e
k
Differentialgleichung: f'(x) = -·f(x)·(S - f(x)) (**)
S
Die momentane Änderungsrate ist proportional zum Produkt
von f(x) und (S-f(x)) (dem "Sättigungsmanko").
f'(x) = 0,1·f(x)·(100 - f(x)) mit f(0) = 50Lösung Man kann nach (*) und (**) sofort ablesen:
k
- = 0,1 und S = 100 => k=10
S
100
f(x) = ———————————— mit f(0)=50 folgt a=1.
-10x
1 + a·e
2. Aufgabe: Ein Bakterienkultur auf einer begrenzten Fläche (Nährboden) wächst proportional zum Produkt des Bestandes und dem Sättigungsmanko. Bei Messung pro Stunde ist der Proportionalitätsfaktor 0,01. Am Anfang ist 1% befallen. Wann sind 99% befallen?
Lösung: Für die Funktion t->f(t) (t ind Stunden, f(t) in % der Fläche) gilt dann
f'(t)=0,001·f(t)·(100 - f(t)).
Von dieser Differentialgleichung (logistisches Wachstum) kennen wir die Lösung
S k
f(t) = ——————————, wobei S=100, - = 0,001 und f(0) = 1. Also ist
-kt S
1 + a·e
100
f(t) = ———————————. Wann ist f(t) = 99 ?
-0,1t
1+99·e
100 -0,1t 1 1
——————————— = 99 => 99·e = —— => -0,1t = ln ——— => t=92
-0,1t 99 2
1+99·e 99
Ergebnis: Nach rund 92 Stunden sind 99% der Fläche befallen.
34. Lektion: Epidemie und Pandemie
34. Lektion: Epidemie (Exponentielles und logistisches Wachstum)
Formeln:
kx
Exponentielles Wachstum: f(x)=A*e
S
Logistisches Wachstum: f(x)=-----------
-kx
1 + a*e
In einem Land verdoppele sich die Zahl der Infizierten alle 3 Tage. Hat man z. B. zum Zeitpunkt 0 eine Anzahl von 1000 Infizierten, so sind es nach 3 Tagen 2000, nach 6 Tagen 4000 Infizierte usw. Die Anzahl der Infizierten wachse also (zunächst) exponentiell.
Berechne einmal für exponentielles Wachstum, das andere Mal für logistisches Wachstum bei einer Population von 80 Millionen die Anzahl der Infizierten nach 27 Tagen und nach 60 Tagen.
Lösung exponentielles Wachstum:
kx
Exponentielles Wachstum: f(x)=A*e
Aus f(0)=1000 folgt A=1000.
3k ln(2)
Aus f(3)=1000*e = 2000 folgt: k= -----
3
Sommit lautet die Formel für das exponentille Wachstum
1
-x
3
f(x)=1000*2
und damit f(27)=1000*29 = 512 000 und f(60) = 1000*220 ≈ 1 Milliarde
Lösung logistisches Wachstum:
S 80Mio
f(x)=-----------, wobei S = 80Mio. Aus f(0)=1000 folgt ------ = 1000
-kx 1 + a
1 + a*e
80Mio
also (angenähert) a=79999. Aus f(3)=2000 folgt ------------ = 2000
-3k
1+79999*e
-ln(0,49999375)
und daraus k=---------------
3
Also f(27)=508 807 (nur eine kleine Abweichung vom exponentiellem Wachstum)
f(60)= 74 330 520 (schon ziemlich nahe der Gesamtpopulation)