Die Homepage von Joachim Mohr
|
Lektionen der Analysis in Aufgaben |

|
| Es handelt sich um "Basisaufgaben" der Analysis, wie sie im Abitur des Gymnasiums in Baden-Württemberg vorausgesetzt werden. |
| Grundlagen |
|---|
| 1. Lektion: Geraden in der x-y-Ebene |
| Ableiten |
| 10. Lektion: Produkt-, Quotienten- und Kettenregel |
| 11. Lektion: Erst umformen, dann ableiten |
| 12. Lektion: Stammfunktionen und Integrale |
| Wichtig bei Kurvendiskussionen |
| 20. Lektion: Asymptoten |
| 21. Lektion: Symmetrien |
|
Wichtig zu merken
Punktsteigungsform und Tangente |
| 22. Lektion: Tangenten und Normale |
| 23. Lektion: Gleichungen von Schaubildern bestimmen |
| 24. Lektion:Exponentialfunktion und Logarithmus |
| 25. Lektion:vermischte Aufgaben |
| Wachstumsfunktionen |
| 30. Lektion: Lineares Wachstum |
| 31. Lektion: Exponentielles Wachstum |
| 32. Lektion: Beschränktes Wachstum Wachstum |
| 33. Lektion: Logistisches Wachstum |
| 34. Lektion: Epidemie / Pandemie |
Hinweis für Analysisanfänger: Falls Du noch keine Exponentialfunktionen kennengelernt hast: Bearbeite zunächst nur die Aufgaben ohne die Funktion x→ex.
Eine Exponentialfunktionen ( = Wachstumsfunktion) x→exp(kx)=ekx mit
1. Lektion: Geraden in der x-y-Ebene
1. Gib die Gleichungen der Geraden an und prüfe,
ob der Punkt X auf ihr liegt.
a) Die Gerade durch P(6|0) Q(0|3). X(10|-2)
b) Die Gerade durch A(2|2) parallel zur Geraden durch B(0|-1) C(1|1). X(10|20)
c) Die Gerade durch Q(0|3) parallel zur x -Achse. X(11|3)
d) Die Gerade durch N(3|0) parallel zur y -Achse. X(3|11)
2. Zeichne die Geraden
2 5
a) y = -x - 2 b) y = 4 - -x c) x = -2
3 6
Lösung
10. Lektion: Produkt-, Quotienten- und Kettenregel
Siehe auch: "Kettenregel"! (Eine ausführliche Darstellung)Leite ab!
2
2 2t 2 3
1 a) f(x) = 2x ·sinx b) g(t) = ———— c) h(x) = (4 - 5x )
sint
2 2
2 2a t 2 3 2 3
2 a) f (x) = 2t xsinx b) g (t) = ————————— c) h (x) = (t - t x )
t a (a-1)cost t
1
- -x
—————— -kt 2
3. a) f(x) = \/2 - 4x b) g(t) = G - ae c) h(x) = (x-1)e
Lösung
11. Lektion: Erst umformen, dann ableiten
Forme erst um und leite dann ab!
3 2
t(x - 2x + 3) 5
a) f (x) = ————————————— b) f(x) = —————————
t 2 2
x (2x - 1)
Lösung
12. Lektion: Stammfunktionen und Integrale
Ermittle die Stammfunktion! Mache stets die Probe durch Ableiten!
5 1 -4x
1. a) f(x) = 5(2x - 4) b) g(t) = -cos2t c) h(x) = 10 - 3e
2
2 5 2 -kt
2. a) f (x) = t(tx - t ) b) g (t) = a·sina t d) h(t) = G - ae
t a
2π 8 ∞
x —— 1
3. a) I sin-dx b) I\/2xdx c) I ———————dx (I = ∫ = Integral)
4 2
0 0 (2x+2)
0
4. Bestimme die Integralfunktion:
1
x - -t x x
2 π
a) I e dt b) I sin-tdt c) I f'(2t)dt (abstrakt!)
2
0 0 0
Lösung
20. Lektion: Asymptoten
Bestimme die Asymptoten der Funktionen:
2 2
2x - 3 x - 2x + 1 x - 2x + 1
1 a) f(x) = —————— b) f(x) = —————————— c) f(x) = ———————————
3 - 4x 2x 2x - 1
1
x - -x
-0.001t e - 3 2
2 a) f(t) = 2 - e b) f(x) = —————— c) f(x) = (1 - 4x)e
x
2 - e
Lösung
21. Lektion: Symmetrien
Für Anfänger:
1. Prüfe, ob die Schaubilder der folgenden Funktionen symmetrisch
zur y-Achse oder symmetrisch zum Ursprung sind.
1 4 2 x
a) f(x) = -x - 2x + 1 b) f(x) = —————
4 3
x + x
2
1 3 2x
c) f(x) = -x - 3x d) f(x) = —————
3 3
x + x
Für Fortgeschrittene:
1
2. a) Zeige: Das Schaubild von f mit f(x) = —————— ist symmetrisch zu x = 2.
x(x-4)
x - 1
b) Zeige: Das Schaubild von f mit f(x) = ————— ist punktsymmetrisch
x - 2
zum Schnittpunkt der beiden Asymptoten.
Lösung
Was Du unbedingt "drauf" haben solltest:
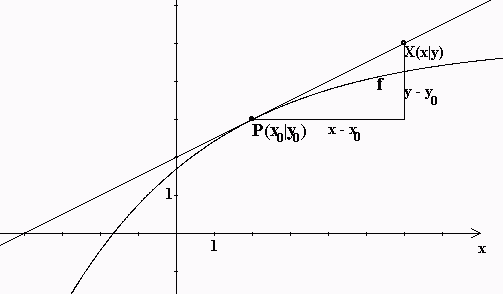
Die Gleichung der Tangente ...
... leitet sich aus der Definition der Steigung ab(Betrachte oben das Steigungsdreieck)
P(x0|y0 sei ein fester Punkt der Tengente
Dann ist Punkt P(x|y) ein Punkt der Tangente, wenn gilt:
y - y
0
m = —————— => y - y = m(x - x )
x - y 0 0
0
Merke!
y = m(x - x ) + y
0 0
(Punktsteigungsform der Geraden)
Die Tangente an das Schaubild von f
hat die Steigung m = f'(x ). Somit
0
Tangentengleichung: y = f'(x )(x - x ) + f(x )
0 0 0
1
Beispiel P(2|3) mit f'(2) = -
2
1 1
Tangente: y = -(x - 2) + 3, also y = -x + 2
2 2
22. Lektion: Tangenten und Normalen
1. a) Bestimme die Gleichung der Tangente und Normalen an das
1 4 2
Schaubild der Funktion f mit f(x) = -x - 2x - x + 1 im Punkt P(1|?)
8
und berechne deren Schnittpunkte mit den Achsen.
1 2 1
b) Dasselbe für f(x)=-(x+1) - - im Punkt P(2|?)
4 4
-x
2. A(u|v) mit u>0 sei ein Punkt des Schaubildes K von f(x) = e . Die
Parallele durch A zur x-Achse schneide die y-Achse in B. Die Tangente
in A an das Schaubild K schneide die y-Achse in C. Für welchen Wert
von u wird der Flächeninhalt des Dreiecks ABC extremal?
3. Vom Punkt P(3|0) soll die Tangente an das Schaubild der Funktion f
2
mit f(x) = - + 2 gelegt werden.
x
Lösung
23. Lektion: Verschiebung von Schaubildern
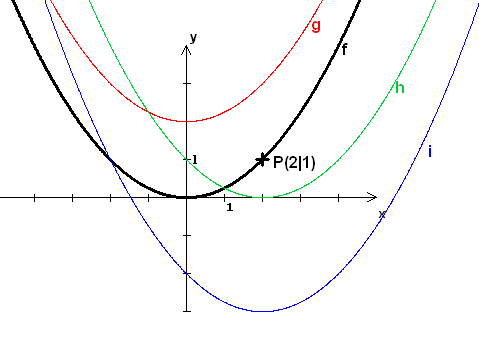 a) Bestimme die Gleichung y=f(x) der Parabel durch den Ursprung O(0|0) und P(2|1), die symmetrisch zur y-Achse ist.
a) Bestimme die Gleichung y=f(x) der Parabel durch den Ursprung O(0|0) und P(2|1), die symmetrisch zur y-Achse ist.
b) Die Parabel von Teil a) wird um +2 in Richtung y-Achse verschoben. Bestimme die Gleichung y=g(x).
c) Die Parabel von Teil a) wird um +2 in Richtung x-Achse verschoben. Bestimme die Gleichung y=h(x).
d) Die Parabel von Teil a) wird um -3 in Richtung y-Achse und um +2 in Richtung x-Achse verschoben. Bestimme die Gleichung y=i(x).
Lösung
24. Lektion: Exponentialfunktion und Logarithmus
1. Aufgabe: Leite ab und vereinfache!
1 3
- -x
3 2x
a) f(x) = e 1 2x e
b) g(x) = (-x + 2)e c) h(x) = ———————
2 2x
e + 1
2. Aufgabe: Vereinfache!
1 1 1 1
-x ln-x -lnx -
2 2 2 x x
a) ln e b) e c) e d) ln(e ·e )
3. Aufgabe: Skizziere in einem Koordinatensystem die Schaubilder der folgenden Funktionen (- 5 ≤ x ≤ 5)!
1 1 1
-x - -x - -x
5 5 5
a) f(x) = e b) g(x) = e c) h(x) = x + e
1
(Rechne mit e ≈ 2,7 und - ≈ 0,4)
e
4. Aufgabe: Gegeben sind die Funktionen
1 1
- -x - -x
2 2
f(x) = x + e und g(x) = x - e
a) Zeige: Für alle x ≥ 0 ist f(x) > g(x).
b) Berechne die ins Unendliche reichende Fläche, die die Schaubilder von f und g im ersten Quadranten einschließen.
5. Aufgabe: Gib die Lösungen der folgenden DGL an!
2
f'(x) = -f(x) mit f(0) = 200
3
Lösung
25. Lektion: vermischte Aufgaben
A1) Das Schaubild einer ganzrationalen Funktion 3.Grades ist
- -
punktsymmetrisch zum Ursprung und hat in T(\/3|-2\/3) einen
Tiefpunkt.
a) Wie kann man die Gleichung der Funktion f ermitteln?
1 3
Ergebnis: f(x)=-x - 3x.
3
b) Ermitteln Sie das Monotonieverhalten der Funktion f an der Stelle x=0,
und erläutern Sie, warum beim Vorzeichenwechsel von f' von
"-" nach "+" ein Minimum vorliegt.
Geben Sie (einfache) Beispiele für Funktionen an, die bei x
0
ein Minimum haben (mit f'(x )=0) und erläutern Sie, ob
0
dort stets f''(x ) >0 ist.
0
c) Skizzieren Sie das Schaubild von g(x)=|x|.
Ist die Funktion überall stetig?
Warum ist die Funktion bei x =0 nicht differenzierbar?
0
Besitzt die Funktion ein Minimum?
tx
A2) Gegeben ist für jedes t∈R die Funktion f (x)=——————
t 2
4 - x
a) Geben Sie den maximalen Definitionsbereich von f an!
Untersuchen Sie das Schaubild auf Symmetrie, Nullstelle
(mit Steigung) und Asymptoten. Skizzieren Sie das Schaubild von
von f . Warum hat das Schaubild keine Hoch- und Tiefpunkte?
4
2
4t +tx
Hinweis: f'(x)=—————————
2 2
(4-x )
b) P(u|v) sei ein Punkt des Schaubildes von f . Die Parallele
4
zur x-Achse durch P schneide die y-Achse in Q, die Parallele
zur y-Achse durch P schneide die x-Achse in R (0 < u < 2).
Der Flächeninhalt des Rechtecks ORPQ sei A(u).
Für welches u ist A(u)=3? Gibt es ein u, für das der
Flächeninhalt extremal wird?
6
A3) Gegeben ist die Funktion f(x)=x-2 - ——— x ∈ R\{1}
x-1
Ihr Schaubild sei K.
a) Bestimmen Sie die maximale Definitionsmenge.
Untersuchen Sie K auf Nullstellen und Asymptoten.
Zeigen Sie: K hat keinen Hoch- und Tiefpunkt.
Skizzieren Sie K.
b) Die Tangente in der Nullstelle N(x |0) mit x >0 und die
0 0
Koordinatenachsen bilden ein Dreieck. Berechne den Flächen-
inhalt des Dreiecks.
c) Geben Sie weitere Beispiele von Funktionen an, die
waagrechte, senkrechte und schiefe Asymptoten besitzen.
d) Es gibt einen Punkt auf K, der zum Ursprung minimalen
Abstand hat. Wie würden Sie diesen Punkt ermitteln?
(Rechnung nicht verlangt, nur Theorie.)
kx
A4) a) Für eine Funktion von der Form f(x)=Ae (x ∈ R) gilt:
f(0)=4 und f'(0)=-8. Bestimmen Sie A und k.
Wo tauchen solche Funktionen (z.B. in den Naturwissenschaften)
auf?
-2x
b) Zeigen Sie: Die Funktion f mit f(x)=4e besitzt keine Hoch-,
Tief- und Wendepunkte. Besitzt sie eine Asymptote?
Skizzieren Sie das Schaubild mit Hilfe der Tangente in P(0|?).
Die Tangente in P(0|4) an das Schaubild von f und die
Koordinatenachsen bilden ein Dreieck. Wie groß sind die
Seitenlängen und Winkel dieses Dreiecks?
kx
c) Bestimme bei der Funktion f mit f(x)=Ae die Parameter
A>0 und k so, daß die Tangente in P(0|?) die x-Achse in A(1|0)
schneidet und parallel zur Geraden mit der Gleichung y=-8x verläuft.
A5) a) Skizzieren Sie die Schaubilder von
1
-x
2 -2x
f (x)=e und f (x)=e x¯ R.
1 -2
-
2
Zeigen Sie, daß sich die Schaubilder in S(0|1) senkrecht schneiden.
Die Tangenten in S sowie die x-Achse bilden ein Dreieck.
Berechnen Sie den Inhalt des Dreiecks.
b) Die Schaubilder der Funktionen von Teil a) und die x-Achse
begrenzen eine ins Unendliche reichende Fläche. Wie
kann man den Flächeninhalt -falls er existiert- berechnen?
c) Wann schneiden sich die Schaubilder von
ax -bx
f (x)=e und f (x)=e (a,b>0) in S(0|1) senkrecht?
a b
d) Die Tangenten in S(0|1) der Schaubilder von
1
- -x
ax a
f (x)=e und f (x)= e , sowie die x-Achse
a 1
- -
a
bilden ein Dreieck. Für welches a>0 ist der Flächeninhalt
dieses Dreiecks extremal? (Lösung: der Flächeninhalt
1 1
F(a)=-(a + -) hat bei a=1 ein absolutes Minimum.)
2 a
-x
A6) Gegeben ist die Funktion f durch f(x)=x+e ; x∈R.
Ihr Schaubild sei K.
a) Bestimmen Sie den Tiefpunkt und die Asymptote von K.
Skizzieren Sie K.
Warum hat K keine Wendepunkte? Was bedeutet dies?
b) Die Kurve K, die y-Achse, die Gerade y=x und die Gerade
x=u (u>0) schließen eine Fläche ein. Berechne Ihren Inhalt.
c) Die Gerade x=t (mit t>0) schneidet K in P und die Gerade y=x
t
in Q . Wie berechnet man dasjenige t, für das der Flächeninhalt
t
des Dreiecks OQ P einen Extremwert annimmt?
t t
-kt
A7) Eine radioaktive Substanz zerfällt nach dem Gesetz f(t)=ae .
(t in Tagen). Zu Anfang waren von der Substanz noch 40g vorhanden,
nach 21 Tagen nur noch 5g.
a) Bestimmen Sie a und k (auf 2 Dezimalen nach dem Komma).
b) Nach wieviel Tagen sind nur noch ein Gramm vorhanden?
c) Nach wieviel Tagen halbiert sich die Substanz (Halbwertszeit)?
d) Wie groß ist die prozentuale Abnahme pro Tag?
1
-t
1 2
A8) a) Skizzieren Sie das Schaubild von f(t)=-¨e .
4
1
Zeigen Sie: f(-4)= ——— .
2
4e
1
b) Eine Population von Insekten besteht heute aus - Millionen
4
1
Individuen, vor vier Jahren waren es nur -- Millionen.
16
kt
Sie entwickelt sich nach der Gesetzmäßigkeit N(t)=ae .
Bestimmen Sie a und k (näherungsweise auf zwei geltende Ziffern).
Wann ist die Population auf das Doppelte wie heute angewachsen?
Lösung
30. Lektion: Lineares Wachstum
Aufgabe: Lena hat einen Smartphonevetrag (mit einer Telefonflatrate) mit einem monatlichen Basistarif. Jede Minute, die sie im Internet ist, wird jedoch abgerechnet. Im ersten Monat bezahlt Sie für 6 Stunden online 18 € im zweiten Monat für 11 Stunden online 22 €. Im dritten Monat ist sie 15 Stunden online. Wie hoch sind dann die Kosten.Lösung
31. Lektion: Exponentielles Wachstum
1.Aufgabe:
Borgland hatte im Jahr 2018 eine Verschuldung von 60% seines Bruttoinlandsprodukts. Seine Verschuldung wächst jährlich um 11 %. Spätestens bei einer Verschuldung von 150% geht dieser Staat bankrott. In welchem Jahr dürfte dieses Ereignis eintreten?2. Aufgabe
Die Frequenzen von Vielfachen eines musikalischen Intervalls wachsen exponentiell:
Intervall Frequenzverhältnis
1 Oktave 2
2 Oktaven 4
3 Oktaven 8
4 Oktaven 16
...
n
n Oktaven 2
Intervalle werden in ihrer Größe als Vielfache von einem Cent angegeben, wobei 1200 Cent = 1 Oktave.
Berechne die Größe einer Quinte in Cent!
Hinweis: Berechne das passende n für Quinte = n·Oktave = 1200·n·Cent mit Hilfe des Frequenzverhältnisses q=3/2 der Quinte.
Lösung
32. Lektion: Beschränktes Wachstum
1. Aufgabe: Bestimmen Sie die Lösung der Differentialgleichungen:a) f'(x) = 0,1·(100 - f(x)) mit f(0) = 100 b) f'(t) = 20 - 0,3·f(t) mit f(0) = 2002. Aufgabe: Wird Salz in Wasser gelöst, ist dies bei einer bestimmten Temperatur nur bis zu einer bestimmten Sättigung möglich. Die Geschwindigkeit wie sich das Salz löst, ist proportional zur Restmenge des noch lösbaren Salzes.
a)Bestimmen Sie die Funktion t→m(t) (t: Zeit in Stunden, m(t) = Prozent der maximal lösbaren Salzmenge) bei einem Proportionalitätsfaktor von k = 3.
b) Wann sind 50% der Sättigung erreicht.
3. Aufgabe: In einer Stadt gibt es 40000 Haushalte, von denen schätzungsweise jeder fünfte für den Kauf eines neu auf den Markt gebrachten Haushaltsartikels in Frage kommt. Es ist damit zu rechnen, dass der Absatz des Artikels im Laufe der Zeit schwieriger wird, da der Kreis der Käufer und deren Kauflust abnimmt. In den ersten drei Monaten werden 1700 Stück des Artikels verkauft.
Kann der Hersteller davon ausgehen, dass innerhalb des ersten Jahres wenigstens 5500 Stück verkauft werden?
4. Aufgabe:
Pegelstand in einem Wasserreservoir:
t→V(t) Volumen des Wassers (t in Minuten, V(t) in Kubikmeter)
bekannt: V(0)=20
3
Zufluss: 0,15 m pro Minute
Abfluss: 0,25% des Inhalts pro Minute.
Bestimme die Funktion t→V(t)
Lösung
33. Lektion: Logistisches Wachstum
1. Aufgabe: Bestimmen Sie die Lösung der Differentialgleichung:f'(x) = 0,1·f(x)·(100 - f(x)) mit f(0) = 50
2. Aufgabe: Ein Bakterienkultur auf einer begrenzten Fläche (Nährboden) wächst proportional zum Produkt des Bestandes und dem Sättigungsmanko. Bei Messung pro Stunde ist der Proportionalitätsfaktor 0,001. Am Anfang ist 1% befallen. Wann sind 99% befallen?
Lösung 34. Lektion: Exponentielles und Logistisches Wachstum
34. Lektion: Epidemie / Pandemie
AufgabeIn einem Land verdoppele sich bei einer Epidemie die Zahl der Infizierten alle 3 Tage. Hat man z. B. zum Zeitpunkt 0 eine Anzahl von 1000 Infizierten, so sind es nach 3 Tagen 2000, nach 6 Tagen 4000 Infizierte usw. Die Anzahl der Infizierten wachse also (zunächst) exponentiell.
Berechne einmal für exponentielles Wachstum, das andere Mal für logistisches Wachstum bei einer Population von 80 Millionen die Anzahl der Infizierten nach 27 Tagen und nach 60 Tagen.
Lösung
