Joachim Mohr   Mathematik Musik
≡

Vorbemerkung: Körpererweiterungen von ℚ

Die Menge ℚ(√2)= {a+b√2|a,b∈ℚ} ist ein Körper, in dem man addieren, subtrahieren, multiplizieren und dividieren (mit Ausnahme durch Null) kann. ℚ(√2) ist auch ein 2-dimensionalere Vektorraum über ℚ. Man sagt: ℚ(√2) ist eine Körpererweiterung von ℚ vom Grade 2.
Entsprechend sind weitere Körpererweiterungen definiert.

Konstruktion mit Zirkel und Lineal

Wir identifizieren unsere Zeichenebene mit der komplexen Zahlenebene ℂ. Wir gehen vom Punkt 0 und 1 aus und überlegen, welche Punkte man in ℂ von diesen beiden Punkten konstruieren kann. Da gehört natürlich die Zahl i mit i2=-1 dazu, da man mit Zirkel und Lineal Senkrechte errichten kann und Strecken abtragen. Mit Zirkel und Lineal kann man alle 4 Rechenarten +,-,· und : durchführen. Also gehören alle Punkte K1={a+bi|a,b∈∈ℚ} dazu. Wir haben also zum Körper ℚ die imaginäre Zahl i adjungiert und den Körper K1=ℚ(i) erhalten.
ℚ(i)={a+bi|a,b∈∈ℚ} hat den Grad 2 über ℚ, da {a+bi|a,b∈∈ℚ} ein 2-dimensionaler Vektorraum über ℚ ist.

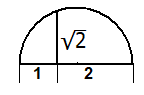wurzel2 Damit wäre das Kapitel "Konstruktion mit Zirkel und Lineal" erledigt, wenn nicht noch die Konstruktion einer Quadratwurzel mit Zirkel und Lineal möglich wäre. Dies ist z.B. mit dem Höhensatz (h2=a·b) möglich. Ich kann also zum Beispiel zu K1 noch √2 adjungieren, allgemein √a für a∈ℚ und a›0.
Der Körper K2=K1(√a) hat den Grad 2 über K1 und damit den Grad 2·2=4 über ℚ, da K2={a+bi+c√a+d√ai|a,b,c,d∈ℚ}. Wir schreiben dafür [K2:ℚ]=4.
Nun kann man noch weitere Wurzeln adjungieren und kann zeigen, dass das Ergebnis in Kn für n=2,3,4,... liegt.
Der Grad der Körpererweiterung ist [Kn:ℚ]=2n.
Zum Beispiel kann die Zahl
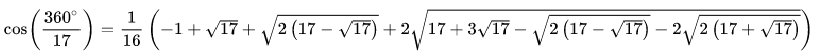
wurzel2
konstruiert werden und damit auch das 17-Eck.
Die Frage, ob sich gewisse Konstruktionen mit Zirkel und Lineal lösen lassen, kann zurückgeführt werden, ob die der Konstruktion zugeordnete Zahl in eine Körpererweiterung von ℚ mit dem Grad 2n für n∈ℕ liegt.
Alle diese Zahlen sind algebraisch, d.h. Nullstellen von Polynomen mit rationalen Koeffizienten.

Die Quadratur des Kreises

Da π eine tranzendente, also keine algebraische Zahl ist (Beweis: Ferdinand von Lindemann 1882), kann man die Kreisfläche π·r2 nicht mit Zirkel und Lineal in ein Quadrat verwandeln.

Die Würfelverdopplung - Das Delische Problem

Man hat einen Würfel mit der Kante 1 und versuche einen Würfel zu konstruieren, der das doppelte Volumen, also das Volumen 2 besitzt.
Der Würfel mit doppelten Volumen hat also die Kantenlänge ∛2.
Adjungiere ich zu ℚ oder zu K1 oder K2 u.s.w.(siehe oben) ∛2, so erhalte ich eine Körpererweiterung vom Grade 3, oder 3·2, oder 3·22 u.s.w.
Die Verdopplung des Volumens eines Würfels mit Zirkel und Lineal ist nicht möglich.

Die Dreiteilung des Winkels

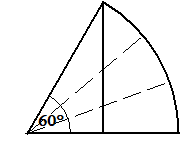winkel60grad Der Winkel von 60° läßt sich mit Hilfe von cos(60°)=1/2 konstruieren.
Könnte mn den Winkel von 60° dreiteilen, könnte man also für α=20° den Wert cos(α) konstruieren.
Nun folgt aus dem Additionstheoren cos(3α)=4(cos(α)3-3cos(α).
Für α=20°, 3α=60° und cos(20°)=x heißt das:
1/2=4x3-3x.
Also ist x=cos(20°) eine Lösung der Gleichung 4x3-6x-1=0.
Das Polynom p=4x3-6x-1 ist über ℚ irreduzibel. Der Zerfällungskörper von p hat den Grad 3.
Also ist Grad[x:ℚ]=3 und daher x nicht mit Zirkel und Lineal konstruierbar.

Konstruktion von Vielecken mit Zirkel und Lineal

Im Juni 1796 konnte man in dem in Jena erscheinenden ”Intelligenzblatt der allgemeinen Literaturzeitung“ unter der Rubrik ”Neue Entdeckungen“ lesen:

Es ist jedem Anfänger der Geometrie bekannt, dass verschiedene ordentliche Vielecke, namentlich das Dreieck, Fünfeck, Fünfzehneck, und die, welche durch ¨ wiederholte Verdopplung der Seitenzahl eines derselben entstehen, sich geometrisch konstruieren lassen.

So weit war man schon zu Euklids Zeit und es scheint, man habe sich seitdem allgemein überredet, dass das Gebiet der Elementargeometrie sich nicht weiter erstrecke: wenigstens kenne ich keinen geglückten Versuch, ihre Grenzen auf dieser Seite zu erweitern. Desto mehr, dünkt mich, verdient die Entdeckung Aufmerksamkeit, dass außer jenen ordentlichen Vielecken noch eine Menge anderer, z. B. das Siebzehneck, einer geometrischen Konstruktion fähig ist. Diese Entdeckung ist eigentlich nur ein Corollarium einer noch nicht ganz vollendeten Theorie von größerm Umfange, und sie soll, sobald diese ihre Vollendung erhalten hat, dem Publikum vorgelegt werden.
        C. F. Gauß aus Braunschweig. Stud. der Mathematik zu Göttingen.

Es verdient angemerkt zu werden, dass Herr Gauß (1777-1855) jetzt in seinem 18ten Jahre steht, und sich hier in Braunschweig mit ebenso glücklichem Erfolge der Philosophie und der klassischen Literatur als der höheren Mathematik gewidmet hat.

Dies war die erste Veröffentlichung von Gauß.
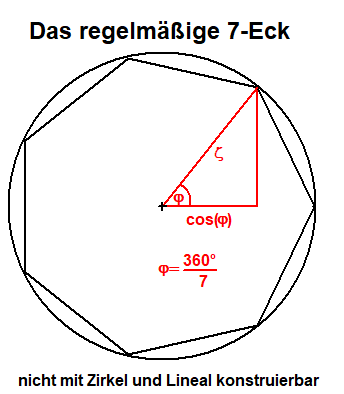
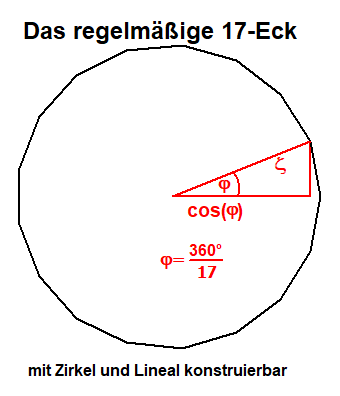
7_eck 17_eck

Die Konstruktion des n-Ecks läuft auf die Konstruktion der Einheitswurzeln - Lösungen von xn=1 - hinaus.

5_eck Die Gleichung xn=1 hat n Lösungen ςk (k=0,1,2,...,n-1) 

          360°        360°       360°
für ς=cis(————) = cos(————)+isin(————)
           n           n          n


 
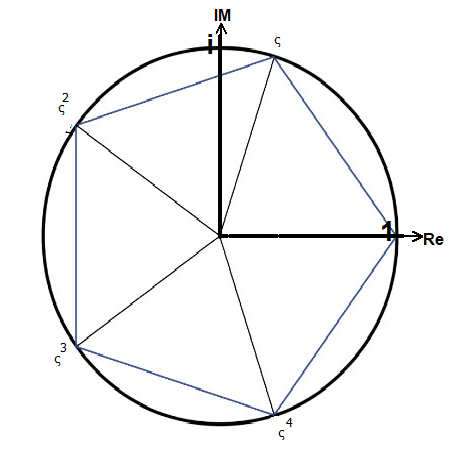
Beispiel: n=5

 0 
ς =1
  
                     ————————
 1          1 — 1   /1 — — 5
ς =cis(72°)=—√5-—+i√ —√5√5+—
            4   4    8     8

 2             
ς =cis(144°) 

 3
ς =cis(216°) 

 

 4             
ς =cis(288°)  

                              1 — 1 
Das Fünfeck kann mit cos(72°)=—√5-— konstruiert werden.
                              4   4

Satz von Gauß (vereinfacht): Das 3-Eck,
das 5-Eck,
das 17-Eck,
das 257-Eck und
das 65537-Eck ist mit Zirkel und Lineal konstruierbar. 

               0         1         2            3                  4
              2         2         2            2                  2 
Die Zahlen 3=2  + 1, 5=2  +1, 17=2  +1, 257 = 2   +1  und 65537 =2  +1
sind Fermatsche Primzahlen, weitere sind bis heute (2023) nicht bekannt.
Da mit Zirkel und Lineal die Eckenzahl eines Vielecks sich verdoppeln läßt und zum Beispiel mit einem ineinander geschachtelten 3-Eck und 5-Eck das 15-Eck konstruieren läßt, kann der oben genannte Satz allgemeiner gefaßt werden.
Satz von Gauß:
Ein n-Eck (n≥3) läßt sich genau dann mit Zirkel und Lineal konstruieren, wenn n von der der Form
n=2k·p1·p2···pm für k∈ℕ0 und paarweise Fermatsche Primzahlen p1,p2,···pm ist.
Der Beweis hierfür kann über die Eulersche φ-Funktion geführt werden.
Sei n≥3 und C={1,ζ,ζ2,...,ζn-1} die Menge der n Einheitswurzeln über ℚ.
Eine primitive Einheitswurzel ist eine Element, das C erzeugt. Das sind die Elemente ζm∈C mit ggT(m,n)=1 (m=1,2,...,n-1).
Ihre Anzahl ist φ(n) (φ: Eulersche Funktion).
Beispiel: {x|x6=1}={cis(k·360°/6)|k=0,1,2,3,4,5}. Nur cis(360°/6) und cis(5·360°/6} sind primitiv ⇒ φ(6)=2.
Man kann beweisen, dass [ℚ(cis(360°/n):ℚ]=φ(n) ist.
Jetzt bleibt nur noch zu zeigen, dass der Erweiterungskörper, in dem die Einheitswurzeln liegen, den Grad einer Zweipotenz hat, dass also φ(n) eine Zweierpotenz ist und das kann nur der Fall sein, wenn n von der oben genannten Form n=2k·p1·p2···pm ist. Dies kann man beweisen. ∎