Joachim Mohr Mathematik Musik Delphi
Die Taylorreihe
f'(0) f''(0) 2 f'''(0) 3
f(x)= f(0) + —————x + ——————x + ———————x + ...
1! 2! 3!
Beweis:
Wir setzten voraus, dass die Funktion f unendlich oft differenzierbar ist und sich in eine Potenzreihe entwickeln läßt:
2 3 4 5
f(x)=a +a x+a x +a x +a x +a x +... f(0)=a
0 1 2 3 4 5 0
2 3 4
f'(x)=a +2a x+3a x +4a x +5a x +... f'(0)=a
1 2 3 4 5 1
2 3
f''(x)=2a +2·3a x+3·4a x +4·5a x + ... f''(0)=2a
2 3 4 5 2
2
f'''(x)=2·3a +2·3·4a x+3·4·5a x + ... f'''(0)=2·3a
3 4 5 3
(4) (4)
f (x)=2·3·4a +2·3·4·5a x+... f (0)=2·3·4a
4 5 4
Mit 0!=1 1!=1, 2!=2, 3!=2·3, 4!=2·3·4, ... folgt
(4)
f(0) f'(0) f''(0) f'''(0) f (0)
a =————, a =—————, a =——————, a = ——————, a =———————, ... ∎
0 0! 1 1! 2 2! 3 3! 4 4!
Die Moivresche Formel
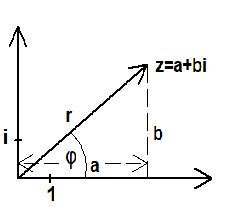Die komplexe Zahl z=a+bi (a,b∈ℝ) kann dargestellt werden als
z=r·(cos(φ)+isin(φ)) "Polarkoordinaten"
————
/2 2
mit r:=√a +b und
b b
tan(φ) = — φ=arctan(—)
a a
a=rcos(φ) b=rsin(φ)
iφ
Die Moivresche Formel e =cos(φ)+isin(φ) folgt aus der Taylorreihe
f'(0) f''(0) 2 f'''(0) 3
f(x)= f(0) + —————x + ——————x + ———————x + ...
1! 2! 3!
Diese konvergiert für die Exponential-, die Kosinus- und die Sinusfunktion für alle x∈ℂ
x 1 1 2 1 3
e = 1 + ——x + ——x + ——x + ...
1! 2! 3!
iφ 1 1 2 1 3 1 4
⇒ e = 1 + ——iφ - ——φ - ——iφ + ——φ - ...
1! 2! 3! 4!
1 2 1 4
cos(φ)=1 - ——φ + ——φ- ...
2! 4!
1 1 3 1 5
sin(φ)= ——φ - ——φ + ——φ + ...
1! 3! 5!
1 2 1 4 1 1 3 1 5
⇒ cos(φ)+isin(φ)=(1 - ——φ + ——φ - ...)+i(——φ - ——φ + ——φ + ...)
2! 4! 1! 3! 5!
1 1 2 1 3 1 4 1 5
= 1 + ——iφ - ——φ - ——iφ + ——φ + ——φ - ...
1! 2! 3! 4! 5!
iφ
=e ∎
Folgerungen
iφ
Mit der Schreibweise: cis(φ) =(cos(φ)+isin(φ)=e
q qiφ
folgt: cis(φ) = cis(qφ) = e (q∈ℚ)
2 2iφ
Beispiel: cis(φ) = cis(2φ) = e
-2 -2iφ
cis(φ) = cis(-2φ) = e
1
—iφ
—————— 1 2
√cis(φ) =cis(—φ) = e
2
1
—iφ
—————— 1 3
∛cis(φ) =cis(—φ) = e
3