Die Homepage von Joachim Mohr

FAQ

Die Heronsche Flächenformel

Satz: Der Flächeninhalt eines Dreiecks mit den Seitenlängen a, b und c beträgt


        ——————————————————           a + b + c
 A  = \/s(s-a)·(s-b)·(s-c) wobei s = —————————
                                         2

Programm "Heron" dazu siehe: Downloadseite unter "Lernprogramme"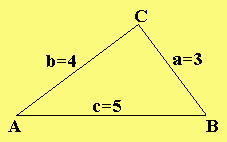

a=3 b=4 c=5

Zum Beispiel errechnet sich der Flächeninhalt eines Dreiecks mit a = 3cm, b = 4cm und c = 5cm

        3 + 4 + 5
mit s = ————————— cm = 6 cm zu
           2

      ——————————————————   2     ——   2       2
A = \/6(6-3)·(6-4)·(6-5) cm  = \/36 cm  = 6 cm

In diesem Fall eines rechtwinkligen Dreiecks hätte man auch rechnen können:



       1       1       2       2
   A = -·a·b = -·3·4 cm  = 6 cm
       2       2

Setzt man s in die Heronsche Formel für A ein und quadriert, so sieht man: Zu zeigen ist:


 2  (a+b+c)·(-a+b+c)·(a-b+c)·(a+b-c)
A = ————————————————————————————————  (*)
                     16

Beweis: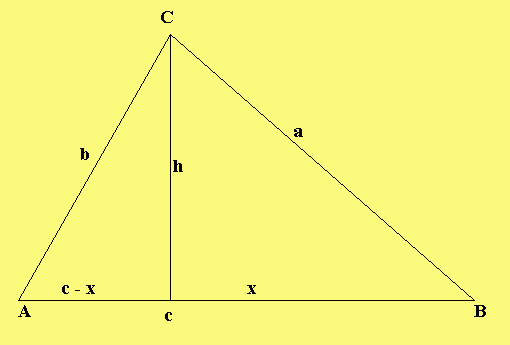
Dreieck

                                      2 2
     c ·h   1                     2  c·h
A  = ———— ( -Grundseite·Höhe) => A = ————
       2    2                         4

Wir versuchen im folgenden h allein durch a, b und c auszudrücken. Dazu verwenden wir verübergehend die Hilfsgröße x.

(Sollte C so liegen, dass die Höhe durch C auf (AB) außerhalb von AB zu liegen kommt, können wir den Beweis mit der Höhe durch A auf BC oder der Höhe durch B auf AC führen.)

Die Rechnung erfolgt geradlinig, ziemlich aufwendig (über die binomischen Formeln) aber nachvollziehbar.

Zur Erinnerung: Die binomischen Formel lauten hier:

(a+c)² = a² + 2ac + c², (c-x)² = c² - 2cx + x², (a+x)·(a-x) = a² - x² und etwas komplizierter

[(a+c) + b)]·[(a+c) - b] = (a+c)² - b² sowie -(a-c)² = -a² + 2ac - c².


     2   2   2      2   2       2       2   2    2   2         2
Mit h = a - x  und h = b - (c-x) folgt a - x  = b - c + 2cx - x

            2    2   2
           a  + c - b
  also x = —————————— .
              2c
                                                 2   2   2          2   2   2
                   2   2   2             (2ac + a + c - b )·(2ac - a - c + b )
Damit ergibt sich h = a - x =(a+x)·(a-x)=————————————————————————————————————
                                                        2
                                                      4c
        2   2     2       2
  [(a+c) - b )]·[b - (a-c) ]     (a+c+b)·(a+c-b)·(b+a-c)·(b-a+c)
= ———————————————————————————  = ———————————————————————————————
                  2                                  2
                4c                                 4c

  (a+b+c)·(a+c-b)·(a+b-c)·(b+c-a)
= ——————————————————————————————— [Beachte beim 4. Faktor: b-(a-c) = b - a + c]
                 2
               4c
                       2  2
                   2  c ·h    (a+b+c)·(a+c-b)·(a+b-c)·(b+c-a)
Somit ergibt sich A = ————— = ———————————————————————————————       ∎
                        4                16

Bemerkung: Heron von Alexandria lebte von 10(?) v. Chr. bis 75(?) nach Chr. Er lehre in Ägypten im legendären Museum von Alexandria Mathematik, Astronomie, Physik, theoretische und praktische Mechanik.

In seinen Werken kann man z.B. nachlesen, wie er mit Hilfe der Beobachtung einer Mondfinsternis die Entfernung Alexandrias von Rom berechnete.

Beim Studium des Zusammenhang von Temperatur und Druck erfand er eine Dampfmaschine (verwendete diese epochemachende Erfindung jedoch nur für Spielereien.)

Bekannt sind auch seine von ihm erdachten Kriegsmaschinen und sein automatisches Theater.

Die Heron'sche Formel befindet sich in seinem erhaltenen Werk "Metrica". Sie stammt jedoch von Archimedes.

Näheres siehe Heron

Koordinaten des dritten Dreieckspunktes

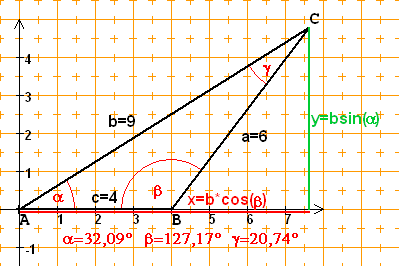
Frage: Bei dem Dreieck A(0|0)B(0|4) sind die Seitenlängen c=AB=4, a=BC=6 und b=AC=9 bekannt. Wie berechnen sich die Koordinaten des dritten Punktes C(x|y) mit y > 0 ?

Antwort: Berechne den Winkel a mit dem Kosinussatz

          2   2   2
         b + c - a    61
cos(a) = ————————— =  ——
           2bc        72

Und dann ist x=b*cos(a) = 7,625   und

                    ————————
                   /    2
y = b*sin(a) = b*\/1-cos (a)

    1
  = -·sqrt(1463) = 4,781
    8

Somit können wir die Koordinaten des
dritten Punktes angeben: C(7,63|4,78)
A(0|0)B(0|4) a=6 b=9

Eine weitere Möglichkeit wäre die Berechnung über die Heronsche Flächenformel

        a+b+c                  ———————————————————
Mit s = ————— = 9,5  folgt A=\/s·(s-a)·(s-b)·(s-c) = 1/4*sqrt(1463)
         2

                            2A
Aus A=2c·h und y=h folgt y= ——  = 1/8*sqrt(1463)
                             c

                           ———————
                          / 2    2
Und nach Pythagoras x = \/ b  - y = 7,625

Mit beiden Lösungen ergeben sich die Formeln für die Koordinaten von C(x|y) zu

     2   2   2
    b + c - a         2A                ———————————————————         a+b+c
x = —————————     y = —— wobei A =  A=\/s·(s-a)·(s-b)·(s-c) mit s = —————
      2c               c                                              2

Berechnung des Flächeninhaltes eines Vierecks

Frage: Ich bin Obmann in einer Kleingartenanlage und möchte die Flächen der 64 Gärten neu berechnen, da wohl ein Fehler in der ursprünglichen Berechnung der Gartengrößen aufgetreten sein muss. Bekannt sind die Seitenlängen der Gärten aber kein Winkel.

Antwort: Allein aus der Länge der vier Seiten ist der Flächeninhalt eines Vierecks nicht bestimmt. Um ihn zu berechnen benötigt man eine weitere Größe (Winkel oder Diagonale).

Die Längeneinheiten LE und zugehörigen Flächeneinheiten FE werden bei den folgenden Berechnungen weggelassen.
LE	1 cm	1 m	10 m	100 m	1 km
FE	1 cm²	1 m²	1 a (Ar)	1 ha (Hektar)	1 km²

Beispiel: a=4; b=2,24; c=3; d=4,47
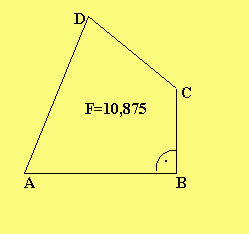Hier hat das Viereck bei B einen rechten Winkel.
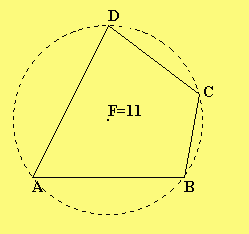Hier beim "Sehnenviereck" hat das Viereck den maximalen Flächeninhalt.
Der minimale Flächeninhalt eines konvexen Vierecks mit den angegeben Maßen ist F= 8,683 (C liegt dann auf BD). Konvex heißt, dass das Viereck keine einspringende Ecke hat, d.h. die Diagonalen verlaufen innerhalb des Vierecks.
Ein weiters Beispiel, das zeigt, dass die Fläche eines Vierecks noch lange nicht aus vorgegeben Seitenlängen berechnet werden kann ist die Raute (Viereck mit vier gleichlangen Seiten). Nehmen wir an, die Seitenlänge der Raute sei a = b = c = d = 4 cm. Das Quadrat mit dem Flächeninhalt 16 cm² ist eine solche Raute. Der Innenwinkel bei A kann jedoch beliebig klein gewählt werden und damit auch der zugehörige Flächeninhalt.

Fälle, in denen man die Vierecksfläche berechnen kann

Im folgenden wird vorausgesetzt, dass die Vierecke keine einspringende Ecke haben.
(Man nennt diese Vierecke "konvex".)

Am besten rechnen Sie dann mit TTMathe Menü "Algebra|rechne Rechenblatt". (Kopieren Sie den folgen Text in das Rechenblatt, ändern Sie Ihre Werte und schon wird die Berechnungen für Sie erledigt.)

I. Man kennt noch eine Diagonale

In diesem Fall kann man das Viereck in zwei Dreiecke zerlegen und von diesen zum Beispiel mit der Heronschen Flächenformel berechnen.

Mit Diagonale e=AC

   Rechenblatt
a=4                             4
b=2,24                          2,24
c=3                             3
d=4,47                          4,47
e=4,92                          4,92
    Teildreieck ABC aus a, b und e
s=(a+b+e)/2                     5,58
I1=sqrt(s*(s-a)*(s-b)*(s-e))    4,408
    Teildreieck CDE aus e, c und d
s=(e+c+d)/2                     6,195
I2=sqrt(s*(s-e)*(s-c)*(s-d))    6,598
    Gesamtfläche
I=I1+I2                         11,006

Mit Diagonale f=BD

         Rechenblatt
a=4                             4
b=2,24                          2,24
c=3                             3
d=4,47                          4,47
f=4,47                          4,47
    Teildreieck ABC aus a, f und d
s=(a+f+d)/2                     6,47
I1=sqrt(s*(s-a)*(s-f)*(s-d))    8,00
    Teildreieck CDE aus b, c und f
s=(b+c+f)/2                     4,855
I2=sqrt(s*(s-b)*(s-c)*(s-f))    3,011
    Gesamtfläche
I=I1+I2                         11,006

II. Das Viereck besitzt einen Rechten Winkel.

In diesem Fall kann man die Diagonale nach Pythagoras berechnen.

Rechter Winkel bei A

         Rechenblatt
a=4
b=2,24
c=3
d=4,47
f=sqrt(a^2+d^2)
    Teildreieck ABC aus a, f und d
s=(a+f+d)/2
I1=sqrt(s*(s-a)*(s-f)*(s-d))
    Teildreieck CDE aus b, c und f
s=(b+c+f)/2
I2=sqrt(s*(s-b)*(s-c)*(s-f))
I=I1+I2

Rechter Winkel bei B

   Rechenblatt
a=4
b=4,1
c=3,9
d=4,2
e=sqrt(a^2+b^2)
    Teildreieck ABC aus a, b und e
s=(a+b+e)/2
I1=sqrt(s*(s-a)*(s-b)*(s-e))
    Teildreieck CDE aus e, c und d
s=(e+c+d)/2
I2=sqrt(s*(s-e)*(s-c)*(s-d))
    Gesamtfläche
I=I1+I2

Rechter Winkel bei C

         Rechenblatt
a=4
b=2,24
c=3
d=4,47
f=sqrt(b^2+c^2)
    Teildreieck ABC aus a, f und d
s=(a+f+d)/2
I1=sqrt(s*(s-a)*(s-f)*(s-d))
    Teildreieck CDE aus b, c und f
s=(b+c+f)/2
I2=sqrt(s*(s-b)*(s-c)*(s-f))
I=I1+I2

Rechter Winkel bei D

   Rechenblatt
a=4
b=4,1
c=3,9
d=4,2
e=sqrt(c^2+d^2)
    Teildreieck ABC aus a, b und e
s=(a+b+e)/2
I1=sqrt(s*(s-a)*(s-b)*(s-e))
    Teildreieck CDE aus e, c und d
s=(e+c+d)/2
I2=sqrt(s*(s-e)*(s-c)*(s-d))
    Gesamtfläche
I=I1+I2

III. Das Viereck ist ein Sehnenviereck

Ein Sehnenviereck ist ein Viereck mit einem Umkreis.

Unter allen Vierecken mit fest vorgegebenen Seitenlängen
hat das Sehnenviereck den größten Flächeninhalt.

Dazu einige Sätze, die für sich schon interessant sind.

Gegenüberliegende Winkel ergeben zusammen 180°
Die Diagonalen eines Sehnenviereckes zerschneiden das Viereck in vier Dreiecke, wobei gegenüberliegende Dreiecke ähnlich sind.
Satz des Ptolemäus: ac+bd=ef
Formel von Brahmagupta (um ca.628 n.Chr.). Für den Flächeninhalt I gilt:
I² = (s-a)(s-b)(s-c)(s-d) für s=(a+b+c+d)/2
Die Diagonalen berechnen sich zu:
e=sqrt((a*c+b*d)*(b*c+a*d)/(a*b+c*d)) und f=sqrt((a*c+b*d)*(a*b+c*d)/(b*c+a*d))
Unter allen Vierecken mit fest vorgegebenen Seitenlängen hat das Sehnenviereck den größten Flächeninhalt.

Wie man sieht, lassen sich die Diagonalen berechnen.

   Rechenblatt
a=4                             4
b=2,24                          2,24
c=3                             3
d=4,47                          4,47
e=sqrt((a*c+b*d)*(b*c+a*d)/(a*b+c*d))  4,920
   f wird nicht benötigt (nur interessehalber:)
f=sqrt((a*c+b*d)*(a*b+c*d)/(b*c+a*d))  4,474
s=(a+b+e)/2                     5,580
I1=sqrt(s*(s-a)*(s-b)*(s-e))    4,408
    Teildreieck CDE aus e, c und d
s=(e+c+d)/2                     6,195
I2=sqrt(s*(s-e)*(s-c)*(s-d))    6,598
    Gesamtfläche
I=I1+I2                         11,006

Noch einfacher ist die Berechnung nach der Formel von Brahmagupta

   Rechenblatt
a=4                             4
b=2,24                          2,24
c=3                             3
d=4,47                          4,47
s=(a+b+c+d)/2                   6,855
I=sqrt((s-a)*(s-b)*(s-c)*(s-d))  11,006

IV. Das Viereck ist ein Trapez

Bei einem Trapez sind zwei Gegenseiten parallel.

Fall (i) a=AB parallel zu d=CD

   Rechenblatt
a=9                                  9
b=4*sqrt(2)                          5,657
c=2                                  2
d=5                                  5
  Mittelparallele
m=1/2*(a+c)                          5,5
  Berechnung von h mit Hilfsgröße x
x=1/2*(a^2+b^2+c^2-d^2-2*a*c)/(a-c)  4
h=sqrt(b^2-x^2)                      4
  Flächeninhalt
I=m*h                                22

Fall (ii) b=BC parallel zu d=AD

   Rechenblatt
a=3                                  3
b=6                                  6
c=5                                  5
d=2                                  2
  Mittelparallele
m=1/2*(b+d)                          4
  Berechnung von h mit Hilfsgröße x
x=1/2*(b^2+c^2+d^2-a^2-2*b*d)/(b-d)  4
h=sqrt(c^2-x^2)                      3
  Flächeninhalt
I=m*h                               12

V Die Koordinaten sind bekannt

Daraus lassen sich alle Abstände berechnen

Für A(a1|a2) B(b1|b2) ist

             —————————————————
    ——      /      2         2
a = AB  = \/(b1-a1) + (b2-a2)

Zum Beispiel berechnet sich der Flächeninhalt I des Vierecks A(20|10)B(60|10)C(70|40)D(10|60) in TTMathe

   Rechenblatt
a1=20                           20
a2=10                           10
b1=60                           60
b2=10                           10
c1=70                           70
c2=40                           40
d1=10                           10
d2=60                           60
a=sqrt((b1-a1)^2+(b2-a2)^2)     40
    Nebenbei bemerkt: TTMathe gibt auch Brüche und Wurzeln aus
b=sqrt((c1-b1)^2+(c2-b2)^2)     31,622 = 10*sqrt(10)
c=sqrt((d1-c1)^2+(d2-c2)^2)     63,246 = 20*sqrt(10)
d=sqrt((d1-a1)^2+(d2-a2)^2)     50,990 = 10*sqrt(26)
e=sqrt((c1-a1)^2+(c2-a2)^2)     58,310 = 10*sqrt(34)
    Teildreieck ABC aus a, b und e
s=(a+b+e)/2                     64,966
I1=sqrt(s*(s-a)*(s-b)*(s-e))    600
    Teildreieck CDE aus e, c und d
s=(e+c+d)/2                     86,272
I2=sqrt(s*(s-e)*(s-c)*(s-d))    1400
    Gesamtfläche
I=I1+I2                         2000

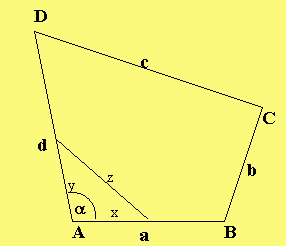
VI Wenn kein Sonderfall vorliegt und keine Diagonale wegen Überbauung meßbar ist

... und auch kein Winkel meßbar ist.

Dann empfehle ich folgendes Verfahren:

Miß x,y und z möglichst genau.
Berechne daraus den passenden Winkel und die zugehörige Diagonale. Hier:

Nach dem Kosinussatz:

 2   2   2
z = x + y - 2xycosα

                2   2    2
               x + y  - z
=> q = cosα = ———————————
                  2xy

 2   2   2
f = a + d - 2adcosα

               2   2
Also f = sqrt(a + d - 2adq)

Mit TTMathe gerechnet:

   Rechenblatt
a=40                            40
b=31,6                          31,6
c=63,2                          63,2
d=51                            51
  zusätzliche Messung für den Winkel a
x=2                             2
y=2,2                           2,2
z=3,24                          3,24
  q = cos(a)
q=(x^2+y^2-z^2)/(2*x*y)         -0,188 364
   alpha wird nicht benötigt (nur interessehalber)
   in TTMathe ist acs(q) bzw.ac_(q) der Arccos im Bogen bzw. Gradmaß
alpha=ac_(q)                    100,857
f=sqrt(a^2+d^2-2*a*d*q)         70,495
    Teildreieck ABC aus a, f und d
s=(a+f+d)/2                     80,747
I1=sqrt(s*(s-a)*(s-f)*(s-d))    1001,741
    Teildreieck CDE aus b, c und f
s=(b+c+f)/2                     82,647
I2=sqrt(s*(s-b)*(s-c)*(s-f))    998,543
    Gesamtfläche
I=I1+I2                         2000

Interessant ist. Mißt man z=3,24 m nur auf 1% genau (etwa 3 cm zu groß oder zu klein), so ist der Inhalt noch auf 0,2% genau. Bei einer Umlage von 100 € bezogen auf den Flächeninhalt werden also 20 Cent zu viel oder wenig erhoben. Verglichen mit Heizungsabrechnungen handelt es sich um eine Präzisionsabrechnung! .