Die Homepage von Joachim Mohr
Frage: Was ist der Unterschied zwischen stetigem Wachstum und diskretem Wachstum?
(lineares, exponentielles und beschränktes Wachstum)
Antwort: stetiges (kontinuierliches) Wachstum bedeutet, dass in jedem Moment etwas hinzukommt (Beispiel: Vermehrung von Bakterien), diskretes Wachstum, dass erst nach jeder Zeiteinheit etwas hinzugeschlagen wird (Beispiel: Zinszahlung).
Häufig dient die Betrachtungsweise des diskreten Wachstums als Näherung des stetigen Wachstums, wenn nur die Zeiteinheit genügend klein gewählt wird.
Ebenso häufig beschreibt man mit stetigem Wachstum die Idealisierung eines diskreten Wachstums (zum Beispiel beim radioaktiven Zerfall das negative Wachstum: die Atome zerfallen diskret, aber in einer Winzigkeit, die zu erfassen sich nur im atomaren Bereich lohnt.)
Ich werde den Unterschied an Hand folgender Wachstumsvorgänge verdeutlichen
- Exponentielles Wachstum
- lineares Wachstum (kein Unterschied zwischen stetig und diskret)
- Beschränktes Wachstum (zwei Beispiele)
Dabei betrachten wir bei I. und II. die Funktion t -> f(t) mit f(0) = a mit a = 100, dem Wachstumsfaktor k mit k = 10% = 1/10 = 0,1 und der Zeiteinheit t mit t = 1 Jahr.
I Exponentielles Wachstum
a) Diskretes Wachstum mit folgender Voraussetzung: f(0) = 100 und nach jedem Jahr kommt 1/10 oder 10% des Bestandes dazu.
f(0) = 100
f(1) = 100 + 10 = 110
f(2) = 110 + 11 = 121
f(3) = 121 + 12,1 = 133,1
f(4) = 133,1 + 13,31 = 146,41
....
Allgemeiner formuliert:
f(0) = 100
1 1
f(1) = 100 + ——·100 = 100·(1 + - )
10 10
1 1
f(2) = f(1) + ——·f(1) = f(1)·(1 + ——)
10 10
1 1 1 2
= 100·(1 + ——)·(1 + ——) = 100·(1 + ——)
10 10 10
1
f(3) = f(2) + ——·f(2)
10
1 1 3
= f(2)·(1 + ——) = 100·(1 + ——)
10 10
...
1 t t
f(t) = 100·(1 + ——) = 100·1,1 (t ganze Zahl)
10
Allgemein:
f(0) = a
f(1) = a·(1 + k)
2
f(2) = a·(1 + k)
...
t
f(t) = a·(1 + k)
b) Stetiges Wachstum mit folgender Voraussetzung:
f(0) = 100 und
in jedem Moment kommt 10% = 1/10 = 0,1 pro Zeiteinheit des Bestandes
dazu.Den letzten Satz müssen wir genau erklären. Es handelt sich um die "momentane Änderungsrate". Sie wird aber ausgedrückt als "Änderung pro Zeiteinheit". Das ist missverständlich, wenn man nicht die genaue Definition kennt.
Auch beim freien Fall, bei dem die Geschwindigkeit zunächst wächst, sagt man: Nach zwei Sekunden ist die momentane Fallgeschwindigkeit 71 km pro Stunde.
Das bedeutet: Ist ein Stein 2 Sekunden frei gefallen, dann legt er in
km
der Zeit Δt die Strecke 71 ——·Δt zurück,
h
zum Beispiel in der Zeit von 0,1 Sekunden
km 1000m
die Strecke von 71——·0,1s = 71·——————·0,1s
h 36000s
= 1,9 m.
Aber genau genommen ist diese Rechnung schon nicht mehr genau, da die Geschwindigkeit
beim freien Fall nach diesen 0,1 weiteren Sekunden schon auf 74 km/h angewachsen ist.Ich versuche das stetige Wachstum beim exponentiellem Wachstum folgendermaßen zu erklären:
1. (grobe) Näherung:
Hat man zu einem Zeitpunkt t den Bestand f(t) so ist
er nach einer Zeiteinheit angewachsen auf ungefähr
1
f(t) + ——f(t). Die Änderung pro Zeiteinheit
10
beträgt also 0,1·f(t).
2. (schon bessere) Näherung:
Hat man zu einem Zeitpunkt t den Bestand f(t)
so ist er nach einer halben
Zeiteinheit angewachsen auf ungefähr
1
f(t) + ——f(t). Die Änderung pro 1/2 Zeiteinheit
20
beträgt also 0,05·f(t).
Nach einer Zeiteinheit beträgt die Änderung
dann 0,05·f(t) + 0,05·f(t + 0,5).
Beachte: Wenn f(t) nicht konstant ist, erhält man im Vergleich zu 1.
einen kleinen Unterschied.
3. (schon ganz gute) Näherung:
Hat man zu einem Zeitpunkt t den Bestand f(t) so ist er nach einer
1 1
———— Zeiteinheit angewachsen auf ungefähr f(t) + ————·f(t)
1000 1000
Dasselbe in Dezimalzahlen:
Hat man zu einem Zeitpunkt t den Bestand f(t) so ist er nach
0.001 Zeiteinheiten angewachsen
1
auf ungefähr f(t) + 0.001· ——·f(t).
10
Die Änderung ist also
1
f(t + 0.001) - f(t)) = 0.001· ——f(t).
10
4. (allgemeine, noch diskrete) Näherung:
Der Zuwachs pro (sehr kleiner) Zeit Δt ist
1
f(t + Δt) - f(t)= Δt·——f(t)
10
oder als Quotient geschrieben:
f(t + Δt) - f(t) 1
———————————————— = ——·f(t)
Δt 10
5. Definition (stetiges Wachstum von 10%):
"In jedem Moment kommt 1/10 pro Zeiteinheit des Bestandes dazu"
bedeutet:
f(t + Δt) - f(t) 1
lim ———————————————— = ——·f(t)
Δt->0 Δt 10
Was links steht ist nichts anderes als die Ableitung
(Schulmathematiker sagen dazu auch "momentane Änderungsrate").
Wir erhalten somit:
1
f'(t) = ——·f(t).
10
Die Lösung dieser Differentialgleichung mit f(0) = 100 ist, wie man leicht nachrechnen kann:
0,1·t
f(t) = 100·e
Allgemein:
f'(t) = k·f(t) mit f(0) = a
kt
f(t) = a·e
Vergleich:
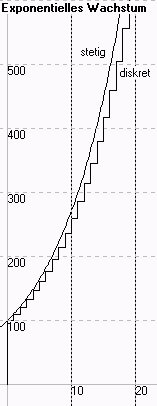
| exponentielles Wachstum | ||
|---|---|---|
| t | diskretes Wachstum | stetiges Wachstum |
| 0 | 100 | 100 |
| 1 | 110 | 110,517 |
| 2 | 121 | 122,14 |
| 3 | 133,1 | 134,986 |
| 4 | 146,41 | 149,182 |
| 5 | 161,051 | 164,872 |
| 6 | 177,156 | 182,212 |
| 7 | 194,872 | 201,375 |
| 8 | 214,359 | 222,554 |
| 9 | 235,795 | 245,96 |
| 10 | 259,374 | 271,828 |
Bemerkung: Würden wir beim stetigen Wachstum die monentane Änderungsrate nicht mit k = 10% sondern nur mit k = ln1,1 = 9,531% angeben, dann hätten wir gleiches Wachstum wie beim dikreten Wachstum mit 10%.
Anders ausgrdrückt: Bei einer momentanen Änderungsrate von 9,531% pro Jahr wächst bei exponentiellem Wachstum ein Bestand durch den Zinseszinseffekt jählich um 10%.
Dann ist
1 t (ln1,1)·t
(1 + ——) = e
10
Allgemein bei jährlichem Wachstumum den Faktor k = 100·k%
t (ln(1+k))·t
(1+k) = e
2 3 4
k k k
Da ln(1+k) = k - —— + —— - —— + ...
2 3 4
folgt für "kleines" k und t:
ln(1+k)≈k und damit (1+k)t ≈ ek·t
Das heißt: Der "Zinseszinseffekt" des stetigen Wachstum ist bei kleinem Wachstumsfaktor und kleiner Zeit
vernachlässigbar.
Vergleich: Diskretes Wachstum und stetiges Wachstum nach einer Zeiteinheit (zum Beispiel nach einem Jahr) bei einem
Angangsbestand von 100:
| diskret | stetig | |
|
100·(1+k) Wachstum ohne "Zinseszinseffekt" |
100·ek Wachstum mit "Zinseszinseffekt" |
|
| k=1% | 101 | 101,01 |
| k=2% | 102 | 102,02 |
| k=3% | 103 | 103,05 |
| k=4% | 104 | 104,08 |
| k=5% | 105 | 105,13 |
| k=6% | 106 | 106,18 |
| k=7% | 107 | 107,25 |
| k=8% | 108 | 108,33 |
| k=9% | 109 | 109,41 |
| k=10% | 110 | 110,52 |
1 2 3
Zur Erinnerung: 1%=———=0,01 , 2% =———=0,02, 3%=———=0,03, ... und
100 100 100
1% von 100 = 1, 2% von 100 = 2, 3% von 100 = 3, ...
II Lineares Wachstum
a) Diskretes Wachstum mit folgender Voraussetzung:
f(0) = 100 undnach jedem Jahr kommt 1/10 oder 10% des Anfangsbestandes dazu.
f(0) = 100 f(1) = 100 + 10 f(2) = 110 + 10 = 120 f(3) = 120 + 10 = 130 .... f(t) = 100 + 10·t
b) Stetiges Wachstum mit folgender Voraussetzung:
f(0) = 100 undin jedem Moment kommt 1/10 oder 10% pro Zeiteinheit des Anfangsbestandes dazu.
Oder:
nach jedem Jahr kommt 10 hinzu.
nach jedem halben Jahr kommt 5 hinzu (Der Zuwachs nach einem Jahr ist wieder 10).
nach je 0.001 Jahren kommt 0.001·10 hinzu (Der Zuwachs nach einem Jahr ist wieder 10). .
...
Es ändert sich nichts. Wie beim diskreten Wachstum erhält man:
f(0) = 100 f(1) = 100 + 10 f(2) = 100 + 20 ... f(t) = 100 + 10·tAllgemein:
f(0) = a f(1) = a·(1+k) ... f(t) = a (1 + k·t)Oder mit m=ak und c = a
f(0) = c f(1) = m + c ... f(t) = m·t + c
Fazit: Beim linearem Wachstum gibt es keinen Unterschied zwischen diskret und stetig.
(Jedenfalls, wenn man nur am Jahresanfang die Werte betrachtet.)
Die Änderung ist proportional zur Zeit.
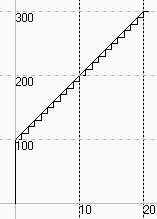
| lineares Wachstum | ||
|---|---|---|
| t | diskretes Wachstum | stetiges Wachstum |
| 0 | 100 | 100 |
| 1 | 110 | 110 |
| 2 | 120 | 120 |
| 3 | 130 | 130 |
| 4 | 140 | 140 |
| 5 | 150 | 150 |
| 6 | 160 | 160 |
| 7 | 170 | 170 |
| 8 | 180 | 180 |
| 9 | 190 | 190 |
| 10 | 200 | 200 |
III Beschränktes Wachstum. Anfangswachstum 10%.
a) Diskretes beschränktes Wachstum mit folgender Voraussetzung:
f(0) = 100 und Grenzwert G= 1000nach jedem Jahr kommt 1/90 oder 1 1/9% des Sättigungsmankos G - f(t) hinzu.
(Das Sättigungsmanko ist der Betrag, der bis zu dem Grenzwert noch fehlt.)
Der Faktor 1/90 wurde gewählt, damit im 1. Jahr 1/10 hinzukommt.
f(0) = 100
1
f(1) = 100 + ——·(1000 - 100) = 110
90
1
f(2) = 110 + ——(1000 - 110) = 119,89
90
1
f(3) = 119,89 + ——·(1000 - 119,89) =129,67
90
1
f(3) = 129,67 + ——·(1000 - 129,67) =139,34
90
1
f(3) = 139,34 + ——·(1000 - 139,34) =128,90
90
...
Herleitung mit der Rekursionsformel:
1 89 100
f(k+1) = f(k) + ——·(1000 - f(k)) = ——·f(k) + ———
90 90 9
89 100
Mit q=—— und v=——— sowie f(k+1) = q·f(k) + v folgt:
90 9
f(0) = 100
f(1) = q·100 + v
2
f(2) = q·(q·100 + v) + v = q ·100 + q·v + v
2 3 2
f(3) = q·(q ·100 + q·v + v) + v = 100q + v(1 + q + q )
...
t 2 3 t-1
f(t) = 100q + v(1 + q + q + q + ... + q )
Mit der Summenformel für geometrische Reihen
t
2 3 t-1 1 - q
1 + q + q + q + ... + q = ——————— ( q≠1) erhält man
1 - q
t
t 1-q 89 t 89 t
f(t) = 100q + v·——— = 1000 - 900·(——) = 1000·(1 - 0,9·(——) )
1-q 90 90
Man sieht: lim f(t) = 1000.
t->∞
Allgemein:
f(0) = a
f(t+1) = f(t) + k(G - f(t)) = f(t)(1-k) + kG
Daraus folgt:
f(0) = a
f(1) = a·(1-k) + kG
2
f(2) = a·(1-k) + kG(1-k) + kG
3 2
f(3) = a·(1-k) + kG((1-k) + (1-k) + 1)
... ( siehe oben geometrische Reihe)
t t t
f(t) = a·(1-k) + G(1 - (1 - k) ) = G - (G - a)·(1-k)
b) Stetiges beschränktes Wachstum mit folgender Voraussetzung:
f(0) = 100 und Grenzwert G = 1000und in jedem Moment kommt 1/90 oder 10/9% des Sättigungsmankos G - f(t) pro Zeiteinheit hinzu.
Wie beim stetigen exponentiellen Wachstum gezeigt wurde, wird dadurch folgende Differentialgleichung definiert.
1
f'(t) = ——·(1000 - f(t)) mit dem Anfangswert f(0) = 100.
90
Die Lösung dieser Differentialgleichung ist - wie man nachrechnen kann -
1
- ——·t
90
f(t) = 1000·(1 - 0,9·e )
Allgemein:
Die Lösung der Differentialgleichung
f'(t) = k·(G - f(t)) mit f(0) = a ist
-kt
f(t) = G - c·e mit c = G - a
Vergleich:
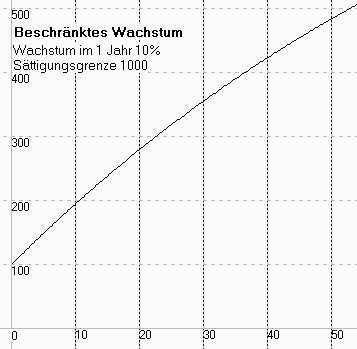
| beschränktes Wachstum | ||
|---|---|---|
| t | diskretes Wachstum | stetiges Wachstum |
| 0 | 100 | 100 |
| 1 | 110 | 109,945 |
| 2 | 119,889 | 119,779 |
| 3 | 129,668 | 129,506 |
| 4 | 139,338 | 139,124 |
| 5 | 148,901 | 148,636 |
| 6 | 158,358 | 158,044 |
| 7 | 167,709 | 167,347 |
| 8 | 176,957 | 176,547 |
| 9 | 186,102 | 185,646 |
| 10 | 195,145 | 194,645 |
VI Beschränktes Wachstum. Anfangswachstum 90%.
In diesem Fall ist das Wachstum schneller. Es kommt jeweils 10% des Sättigungsmankos hinzu.a) Diskretes beschränktes Wachstum mit folgender Voraussetzung:
f(0) = 100 und Grenzwert G= 1000nach jedem Jahr kommt 1/10 oder 10% des Sättigungsmankos G - f(t) hinzu.
(Das Sättigungsmanko ist der Betrag, der bis zu dem Grenzwert noch fehlt.)
f(0) = 100
f(1) = 100 + 0,1·(1000 - 100) = 190
f(2) = 190 + 0,1·(1000 - 190) = 271
f(3) = 271 + 0,1·(1000 - 271) = 343,9
...
Herleitung mit der Rekursionsformel:
f(k+1) = f(k) + 0.1·(1000 - f(k)) = 0,9·f(k) + 100
f(0) = 100
f(1) = 0,9·100 + 100
2
f(2) = 0,9·(0,9·100 + 100) + 100 = 100·(1 + 0,9 + 0,9 )
2 2 3
f(3) = 0,9·(100·(1 + 0,9 + 0,9 ) + 100 = 100·(1 + 0,9 + 0,9 + 0,9 )
Mit der Summenformel für geometrische Reihen
n+1
2 3 n 1 - q
1 + q + q + q + ... + q = ———————— ( q≠1) erhält man
1 - q
t+1
1 - 0,9 t + 1 t
f(t) = 100·———————— = 1000·(1 - 0,9 ) = 1000 - 900·0,9
1 - 0,9
Man sieht: lim f(t) = 1000.
t->∞
b) Stetiges beschränktes Wachstum mit folgender Voraussetzung:
f(0) = 100 und Grenzwert G= 1000und in jedem Moment kommt 1/10 oder 10% des Sättigungsmankos G - f(t) hinzu.
Wie beim stetigen exponentiellen Wachstum gezeigt wurde, wird dadurch folgende Differentialgleichung definiert.
f'(t) = 0,1·(1000 - f(t)) mit dem Anfangswert f(0) = 100.
Die Lösung dieser Differentialgleichung ist - wie man nachrechnen kann -
-0,1·t
f(t) = 1000·(1 - 0,9·e ) [Allgemeiner Fall: siehe III]
Vergleich:
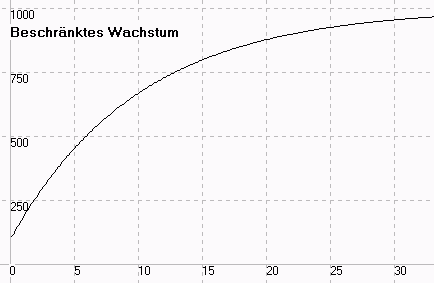
| beschränktes Wachstum | ||
|---|---|---|
| t | diskretes Wachstum | stetiges Wachstum |
| 0 | 100 | 100 |
| 1 | 190 | 185,646 |
| 2 | 271 | 263,142 |
| 3 | 343,9 | 333,264 |
| 4 | 409,51 | 396,712 |
| 5 | 468,559 | 454,122 |
| 6 | 521,703 | 506,07 |
| 7 | 569,533 | 553,073 |
| 8 | 612,58 | 595,604 |
| 9 | 651,322 | 634,087 |
| 10 | 686,189 | 668,909 |
