Die Homepage von Joachim Mohr
Anleitung zum Erstellen von Tonbeispielen
|
|
Download |
|
TTMusik erstellt Tondateien in reiner, mitteltöniger, wohltemperierter und gleichstufiger Stimmung und macht dadurch die Unterschiede hörbar. Beispiel; A-Dur-Dreiklang
Wenn Sie im Programm auf das Menü "Beispiele" klicken, lernen Sie intuitiv, wie sie Musikstücken eingeben und analysieren können.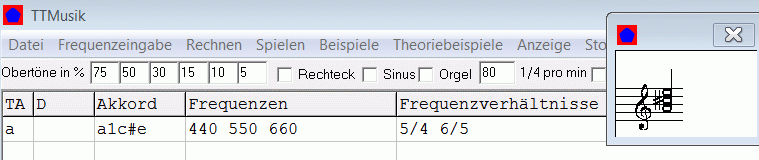
spiele rein
Keine Schwebungen hörbar. Tonartbezeichnung in TTMusik für A-Dur/moll TA=a
spiele mitteltönig
leichtes "Vibrato" der mitteltönigen Quinte. Tonartbezeichnung für A-Dur/moll TA=ma
(TA=mx steht für viele wohltemperierte Stimmungen. TA=ma: mitteltönig, TA=me: Werkmeister III usw.)
spiele gleichstufig
klingt rau. Tonartbezeichnung gleichstufig TA=m~
Keine Schwebungen hörbar. Tonartbezeichnung in TTMusik für A-Dur/moll TA=a
spiele mitteltönig
leichtes "Vibrato" der mitteltönigen Quinte. Tonartbezeichnung für A-Dur/moll TA=ma
(TA=mx steht für viele wohltemperierte Stimmungen. TA=ma: mitteltönig, TA=me: Werkmeister III usw.)
spiele gleichstufig
klingt rau. Tonartbezeichnung gleichstufig TA=m~
Zahlreiche Hörbeispiele von TTMusik auch in Lektionen zur Musiktheorie.
Neu:
September 2015: Nun können die Notenbezeichnungen im Eulerschen Tonnetz ermittelt werden.
Beispiel: Verminderter Septakkord, enharmonisch verwechselt

Die vorkommenden Intervalle sind:
reine kleine Terz
(Frequenzverhältnis 6/5 entspricht 316 Cent)
pythagoreische kleine Terz
(Frequenzverhältnis 32/27 entspricht 294 Cent, ein Terzkomma tiefer)
übermäßige Sekunde
(Frequenzverhältnis 75/64 entspricht 274 Cent, noch ein Terzkomma tiefer)
| Tonart | Akkord | Frequenzen | Frequenzverhältnisse |
| Es-Dur/moll | as 'ces ,d f | 417,2 500,6 586,7 704 | 6/5 75/64 6/5 |
| ,g b es | 391,1 469,3 625,8 | 6/5 4/3 | |
| C-Dur/moll | 'as ,h d f | 422,4 495 594 704 | 75/64 6/5 32/27 |
| g c ,e | 396 528 660 | 4/3 5/4 | |
| A-Dur/moll | ,gis h d 'f | 417,7 501,2 594 712,8 | 6/5 32/27 6/5 |
| a ,cis e | 445,5 556,9 668,3 | 5/4 6/5 | |
| Fis-Dur/moll | gis h 'd ,eis | 422,9 501,2 601,4 704,8 | 32/27 6/5 75/64 |
| ,ais cis fis | 469,9 563,8 751,8 | 6/5 4/3 |
März 2013: TTmusik berechnet den Anteil von Oktaven (Ok), Quinten (Q) und Terzen (T):
| Frequenzv. | in Cent | Ok-Q-T | Intevall |
| 9/8 | 203, 9100 | 2Q-Ok | C-D |
| 10/9 | 182,4037 | -2Q+T+Ok | C-,D |
| 81/80 | 21 ,5063 | 4Q-T-2Ok | C-'C |
| 27/25 | 133,2376 | 3Q-2T-Ok | C-''Des |
| 625/576 | 141, 3449 | -2Q+4T | C-,,,,Cisis |
| 1125 /1024 | 162,8511 | 2Q+3T-2Ok | C-,,,Cisis |
| ... |
Juni 2010 Weitere wohltemperierte Stimmungen integriert, auch vielleicht die von J.S.Bach
März 2003 TTmusik schreibt Noten und zeichnet Frequenzbilder
Februar 2003: Differenztöne können hörbar gemacht werden
Juni 2001: Erste Veröffentlichung
Downloadseite
Mit "TTMusik" können Sie mehrere Töne zu vorgegebenen Frequenzen gleichzeitig erklingen lassen. Das Spektrum der Obertöne können Sie frei angeben. (Vom reinen Sinuston bis zum Zungenregister einer Orgel).
In diesem Sinne ist "TTMusik" eine Erweiterung des Programms "Ton". (Wenn Sie "TTMusik" in den selben Ordner wie "Ton" kopieren, kann dieses von "Ton" aus direkt per Buttondruck aufrufen werden.)
"TTMusik" dient aber eigentlich einem viel anspruchsvolleren Ziel:
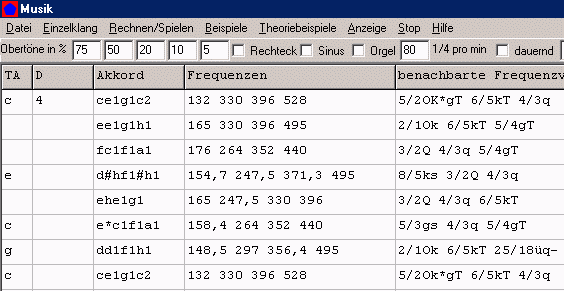 |
| Ok = Oktave, Q = Quinte, q = Quarte, gT = große Terz, ..., - = ein Komma tiefer |
Kurzbeschreibung:
"TTMusik" macht den Unterschied zwischen reiner, mitteltöniger und gleichschwebender Stimmung hörbar.
Und: "TTMusik" analysiert die Akkorde eines Musikstücks: Wenn Sie dabei in reiner Stimmung den Akkord einer falschen Tonart zuordnen, hören Sie es (vielleicht) am "Wolf"sklang und sehen es (mit Sicherheit) an den großen Frequenzverhältnissen.
Sie erfahren, wie sich eine "Kommafalle" anhört und wie man sie als Chorleiter vermeiden kann.
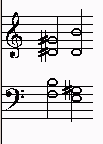 |
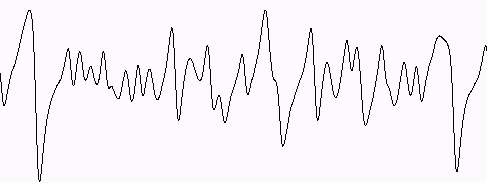 |
Noten- und Schwingungsbilder (äußerst exakt) werden gezeichnet.
|
Aus der Proportion ...
... wird der Centwert, der Tripellogarithmus (Sigel) und der entsprechende Ton berechnet.| Verhältn. | Cent | Sigel | Ton | Probe: | |
| Be rech nung aus Sigel | Be rech nung aus Ton | ||||
| 9/8 | 203, 9100 | 2Q-Ok | D | (3/2)^(+2) *(5/4)^0 *2^(-1) | = (3/2)^2/2 |
| 10/9 | 182, 4037 | -2Q+T+Ok | D-1 | (3/2)^(-2) *(5/4)^(+1) *2^(1) | = (3/2)^(-2)*(5/4)*2 |
| 81/80 | 21, 5063 | 4Q-T-2Ok | C+1 | (3/2)^(4) *(5/4)^(-1) *2^(-2) | = (3/2)^4 *(5/4)^(-1)/4 |
| 27/25 | 133, 2376 | 3Q-2T-Ok | Des+2 | (3/2)^(3) *(5/4)^(-2) *2^(-1) | = (3/2)^3*(5/4)^(-2)/2 |
| 625/576 | 141, 3449 | -2Q+4T | Cisis-4 | (3/2)^(-2) *(5/4)^(4) *2^(0) | = (3/2)^14 *(81/80) ^(-4)/256 |
| 1125/1024 | 162, 85112 | Q+3T-2Ok C | isis-3 ( | 3/2)^(2) *(5/4)^(3) *2^(-2) | = (3/2)^14*(81/80)^(-3)/256 |
| 3456 /3125 | 174, 29643 | Q-5T E | seses+5 ( | 3/2)^(3) *(5/4)^(-5) *2^(0) | = (3/2)^(-17)*(81/80)^(+5)*1024 |
| *(3/2) | *(2/3) pro Stufe | |
| 0 C | 0 C | 1Ok 2 |
| 1 G | 1 F | 2Ok 4 |
| 2 D | 2 B | 3Ok 8 |
| 3 A | 3 Es | 4Ok 16 |
| 4 E | 4 As | 5Ok 32 |
| 5 H | 5 Des | 6Ok 64 |
| 6 Fis | 6 Ges | 7Ok 128 |
| 7 Cis | 7 Ces | 8Ok 256 |
| 8 Gis | 8 Fes | 9Ok 512 |
| 9 Dis | 9 Bes 1 | 0Ok 1024 |
| 10 Ais 1 | 0 Eses | |
| 11 Eis 1 | 1 Asas B | eispiel: |
| 12 His 1 | 2 Deses D | eses-2 bedeutet: |
| 13 Fisis 1 | 3 Geses | Deses um 2 syntonische Komma tiefer |
| 14 Cisis 1 | 4 Ceses C | eses+2 bedeutet: |
| 15 Gisis 1 | 5 Feses | Ceses um 2 syntonische Komma höher |
| 16 Disis 1 | 6 Beses | |
| 17 Aisis 1 | 7 Eseses | |
| 18 Eisis 1 | 8 Asasas | |
| 19 Hisis 1 | 9 Deseses | |
| 20 Fisisis 2 | 0 Geseses |
Modulationen werden "berechnet"
Der Programmpunkt "Modulationen" im TTmusik berechnet die Abweichungen der Töne bei Modulationen in andere Tonarten. Dabei sind folgende Modulationen erlaubt:
T: Modulation in die Paralleltonart um eine Terz höher.
t: Modulation in die Paralleltonart eine Terz tiefer.
Q: Modulation eine Quinte höher (in Richtung Dominante.)
q: Modulation eine Quinte tiefer (in Richtung Subdominate.)
m: Modulation Dur in Moll und umgekert.
Ergänzend ist noch möglich:
+: Rückung um ein Terzkomma höher.
-: Rückung um ein Terzkomma tiefer.
Beispiele: Von C-dur die Modulation in die Paralleltonart e-Moll (um eine Terz höher):
|
C d e f g a h Dur
e fis(D) g a h c d moll (eine Terz höher) |
"S" bedeutet entsprechend: Erniedrigung des Tones in Richtung Subdominattonart.
Von C-moll die Modulation in die Paralleltonart Es-Dur (um eine Terz höher):
|
c d es f g as b moll
Es f+(d) g as b c d Dur (eine Terz höher) |
'-' und "s" bedeutet entsprechend: Erniedrigung des Tones (in Richtung Subdominattonart).
Von C-dur die Modulation in die Paralleltonart a-Moll (um eine Terz tiefer):
|
C d e f g a h Dur
a h c d-(s) e f g moll (eine Terz tiefer) |
Von C-moll die Modulation in die Paralleltonart As-Dur (um eine Terz tiefer):
|
c d es f g as b moll
As b c des(S) es f g Dur (eine Terz tiefer) |
Von C-dur nach G-Dur (um eine Quinte höher):
|
C d e f g a h Dur
G a+(d) h c d e fis(D) Dur (eine Quinte höher) |
|
C d e f g a h Dur
e fis(D) g a h c d moll (eine Terz höher) G a+(d) h c d e fis(D) Dur (eine Terz höher) |
Von C-moll nach g-moll (um eine Quinte höher):
|
c d es f g as b moll
g a(D) b c d es f+(d) moll (eine Quinte höher) |
Von C-dur nach F-Dur (um eine Quinte tiefer):
|
C d e f g a h Dur
F g a b(S) c d-(s) e Dur (eine Quinte tiefer) |
|
C d e f g a h Dur
a h c d-(s) e f g moll (eine Terz tiefer) F g a b(S) c d-(s) e Dur (eine Terz tiefer) |
Von C-moll nach f-moll (um eine Quinte tiefer):
| c d es f g as b moll f g as b-(s) c des(S) es moll (eine Quinte tiefer) |
Von C-dur nach c-Moll:
|
C d e f g a h Dur
c d es+(Sd) f g as+(Sd) b+(Sd) moll (Wechsel Dur-moll) |
Von C-moll nach C-Dur:
| c d es f g as b moll C d e-(Ds) f g a-(Ds) h-(Ds) Dur (Wechsel Dur-moll) |
Bemerkenswert ist hier, dass der Halbtonschritt eine anderer ist als der Halbtonschritt bei den bisherigen Modulationen. Er ist um ein Terzkomma kleiner.
Beim harmonischen Fortschreiten werden die Änderung der Töne immer zur Ausgangstonart angezeigt.
Beispiel:Eine kühne Modulation von e-Moll nach Es-Dur.
Wie ist diese zu deuten?
TTMusik schlägt zwei Möglichkeiten vor.
1. Möglichkeit (siehe "c-moll nach Ces-Dur":tqqq):
Die nicht erklingenden Tonarten sind eingerückt.
Zu beachten wäre noch, dass der Es-Dur-Dreiklang auch in C-Moll, g-Moll, B-Dur und As-Dur rein erklingt. Da es sich um Es-Dur-nahe Tonarten handelt, ist dies bei unseren Überlegungen unerheblich.
|
e fis g a h c d moll
C d e f(S) g a h Dur (eine Terz tiefer) F(S) g a b(S) c d-(s) e Dur (eine Quinte tiefer) B(S) c d-(s) es(S) f(S) g-(s) a Dur (eine Quinte tiefer) Es(S) f(S) g-(s) as(S) b(S) c-(s) d-(s) Dur (eine Quinte tiefer) |
2. Möglichkeit (siehe "c-moll nach Ces+-Dur":Tmt).
|
e fis g a h c d moll
G a+(d) h c d e fis Dur (eine Terz höher) g a+(d) b+(Sd) c d es+(Sd) f+(Sd) moll (Wechsel Dur-moll) Es+(Sd) f+(Sd) g as+(dS) b+(Sd) c d Dur (eine Terz tiefer) |
Was letztendlich richtig ist, erweist sich erst, wenn man den Rückweg in die Ausgangstonart des Komponisten betrachtet. Beachtet man dies nicht, kann man unweigerlich in die "Kommafalle" geraten.
