Joachim Mohr Mathematik Musik Delphi

Kosinus-, Sinus und Tangenswerte

Um zum Beispiel ein regelmäßiges Fünfeck mit Zirkel und Lineal konstruieren zu können, muss sich sin(18°) durch einen Ausdruck darstellen lassen, der - ausgehend von den natürlichen Zahlen - nur die vier Grundrechenarten und die Quadratwurzel enthält.

Hier sind einige nützliche Werte und Zusammenhänge aufgelistet.

Einige Beziehungen werden exemplarisch hergeleitet, alle übrigen wurden mit Maple auf Exaktheit geprüft.

In einem Diskussionsforum (de.sci.mathematik) wurden von Hermann Kremer folgende Werte gepostet.
sin( 0°) = 0
cos( 0°) = 1
sin( 3°) = (sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(sqrt(5)+5))/16
cos( 3°) = (2*(sqrt(3)+1)*sqrt(5+sqrt(5))+sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1))/16
sin( 6°) = (sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))/8
cos( 6°) = (sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))/8
sin( 9°) = (sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))/8
cos( 9°) = (sqrt(2)*(sqrt(5)+1)+2*sqrt(5-sqrt(5)))/8
sin(12°) = (sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))/8
cos(12°) = (sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+sqrt(5)-1)/8
sin(15°) = sqrt(2)*(sqrt(3)-1)/4
cos(15°) = sqrt(2)*(sqrt(3)+1)/4
sin(18°) = (sqrt(5)-1)/4
cos(18°) = sqrt(2)*sqrt(sqrt(5)+5)/4
sin(21°) = (2*(sqrt(3)+1)*sqrt(5-sqrt(5))-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1))/16
cos(21°) = (2*(sqrt(3)-1)*sqrt(5-sqrt(5))+sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1))/16
sin(22,5°) = 1/2*sqrt(2-sqrt(2))
cos(22,5°) = 1/2*sqrt(2+sqrt(2))
sin(24°) = (2*sqrt(3)*(sqrt(5)+1)-sqrt(2)*(sqrt(5)-1)*sqrt(5+sqrt(5)))/16
cos(24°) = (sqrt(2)*sqrt(3)*(sqrt(5)-1)*sqrt(5+sqrt(5))+2*(sqrt(5)+1))/16
sin(27°) = ((sqrt(5)+1)*sqrt(sqrt(5)+5)+(sqrt(5)-1)*(sqrt(5-sqrt(5))-2*sqrt(2)))/16
cos(27°) = ((sqrt(5)+1)*sqrt(sqrt(5)+5)+(sqrt(5)-1)*(sqrt(5-sqrt(5))+2*sqrt(2)))/16
sin(30°) = 1/2
cos(30°) = sqrt(3)/2
sin(33°) = (2*(sqrt(3)-1)*sqrt(sqrt(5)+5)+sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1))/16
cos(33°) = (2*(sqrt(3)+1)*sqrt(sqrt(5)+5)-sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1))/16
cos(36°) = (sqrt(5)+1)/4
sin(36°) = sqrt(2)*sqrt(5-sqrt(5))/4
sin(39°) = (sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)-2*(sqrt(3)-1)*sqrt(5-sqrt(5)))/16
cos(39°) = (sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))/16
sin(42°) = (sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1))/8
cos(42°) = (sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)-1))/8
sin(45°) = sqrt(2)/2
cos(45°) = sqrt(2)/2

Beispiel:

Ein Beispiel ist die Konstruktion des regelmäßigen n-Ecks, etwa des regelmäßigen 5-Ecks. Bei diesem kann man den Mittelpunktswinkel von 72° mit Hilfe der Formel

                     -
                   \/5 -1
cos(72°)=sin(18°)= ——————
                     4

mit Zirkel und Lineal konstruieren.

Carl Friedrich Gauss ...

... fand im Alter von 17 Jahren den Wert
cos(360°/17)=
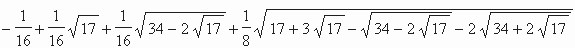
7siebzehneck

=(-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17) -sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16

womit er zeigte, dass das 17-Eck mit Zirkel und Lineal konstruierbar ist. (Siehe beim 5-Eck den Abschnitt "Fermatsche Primzahlen".)

Gegenbeispiel:

sin(10°) lässt sich nicht mit Zirkel und Lineal konstruieren (siehe unten) und damit auch nicht ein regelmäßiges, 36-, 18- oder Neuneck mit den Mittelpunktswinkeln 10°, 20° oder 40°.

Anders ausgedrückt: Die Dreiteilung eines 30°- ,60°- oder 120°-Winkels ist mit Zirkel und Lineal unmöglich.

Die folgenden Werte wurden vom Programm TTMathe (heuristisch) bestimmt. Ihre Exaktheit durch Maple überprüft.
Exemplarische Herleitungen: siehe weiter unten.
sin(0°) = 0
sin(3°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
sin(4,5°) = 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5+sqrt(5))-(sqrt(5)-1)*sqrt(2+sqrt(2)))
sin(6°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
sin(7,5°) = 1/4*(-sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2))) (Beweis: Siehe unten)
sin(9°) = 1/8*(sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))
sin(12°) = 1/8*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
sin(13,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5-sqrt(5))-(sqrt(5)+1)*sqrt(2-sqrt(2)))
sin(15°) = 1/4*sqrt(2)*(sqrt(3)-1)
sin(18°) = (-1+sqrt(5))/4
sin(21°) = 1/16*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
sin(22,5°)= 1/2*sqrt(2-sqrt(2))
sin(24°) = 1/8*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(27°) = 1/8*(-sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
sin(30°) = 1/2
sin(31,5°)= 1/8*(-sqrt(2)*sqrt(2-sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2+sqrt(2)))
sin(33°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)+2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
sin(36°) = 1/4*sqrt(2)*sqrt(5-sqrt(5))
sin(37,5°)= 1/4*(sqrt(3)*sqrt(2+sqrt(2))-sqrt(2-sqrt(2)))
sin(39°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)-2*(sqrt(3)-1)*sqrt(5-sqrt(5)))
sin(40,5°)= 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5+sqrt(5))+(sqrt(5)-1)*sqrt(2+sqrt(2)))
sin(42°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1))
sin(45°) = 1/2*sqrt(2)
sin(48°) = 1/8*(sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)-1))
sin(49,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5+sqrt(5))-(sqrt(5)-1)*sqrt(2-sqrt(2)))
sin(51°) = 1/16*(sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
sin(52,5°)= 1/4*(sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2)))
sin(54°) = (1+sqrt(5))/4
sin(57°) = 1/16*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1)+2*(sqrt(3)+1)*sqrt(5+sqrt(5)))
sin(58,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2-sqrt(2)))
sin(60°) = 1/2*sqrt(3)
sin(63°) = 1/8*(sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
sin(66°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))+(sqrt(5)+1))
sin(67,5°)= 1/2*sqrt(2+sqrt(2))
sin(69°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)+2*(sqrt(3)-1)*sqrt(5-sqrt(5)))
sin(72°) = 1/4*sqrt(2)*sqrt(5+sqrt(5))
sin(75°) = 1/4*sqrt(2)*(sqrt(3)+1)
sin(76,5°)= 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2+sqrt(2)))
sin(78°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+(sqrt(5)-1))
sin(81°) = 1/8*(sqrt(2)*(sqrt(5)+1)+2*sqrt(5-sqrt(5)))
sin(82,5°)= 1/4*(sqrt(3)*sqrt(2+sqrt(2))+sqrt(2-sqrt(2)))
sin(84°) = 1/8*(sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(85,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5+sqrt(5))+(sqrt(5)-1)*sqrt(2-sqrt(2)))
sin(87°) = 1/16*(sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1)+2*(sqrt(3)+1)*sqrt(5+sqrt(5)))
sin(90°) = 1
cos(0°) = 1
cos(3°) = 1/16*(sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1)+2*(sqrt(3)+1)*sqrt(5+sqrt(5)))
cos(4,5°) = 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5+sqrt(5))+(sqrt(5)-1)*sqrt(2-sqrt(2)))
cos(6°) = 1/8*(sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
cos(7,5°) = 1/4*(sqrt(3)*sqrt(2+sqrt(2))+sqrt(2-sqrt(2)))
cos(9°) = 1/8*(sqrt(2)*(sqrt(5)+1)+2*sqrt(5-sqrt(5)))
cos(12°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+(sqrt(5)-1))
cos(13,5°)= 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2+sqrt(2)))
cos(15°) = 1/4*sqrt(2)*(sqrt(3)+1)
cos(18°) = 1/4*sqrt(2)*sqrt(5+sqrt(5))
cos(21°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)+2*(sqrt(3)-1)*sqrt(5-sqrt(5)))
cos((21 3/17)°)=cos(360°/17))=(-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17) -sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16 (17-Eck)
cos(22,5°)= 1/2*sqrt(2+sqrt(2))
cos(24°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))+(sqrt(5)+1))
cos(27°) = 1/8*(sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
cos(30°) = 1/2*sqrt(3)
cos(31,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2-sqrt(2)))
cos(33°) = 1/16*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1)+2*(sqrt(3)+1)*sqrt(5+sqrt(5)))
cos(36°) = (1+sqrt(5))/4
cos(37,5°)= 1/4*(sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2)))
cos(39°) = 1/16*(sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
cos(40,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5+sqrt(5))-(sqrt(5)-1)*sqrt(2-sqrt(2)))
cos(42°) = 1/8*(sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)-1))
cos(45°) = 1/2*sqrt(2)
cos(48°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1))
cos(49,5°)= 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5+sqrt(5))+(sqrt(5)-1)*sqrt(2+sqrt(2)))
cos(51°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)-2*(sqrt(3)-1)*sqrt(5-sqrt(5)))
(cos51 1/7°)=cos(360°/7)=1/12*w+7/(3*w)-1/6 für w:=∛(28+84*I*sqrt(3)) (beweist die Nichtkontruierbarkeit des 7-Ecks):
cos(360°/7)=1/12*w+7/(3*w)-1/6 für w:=∛(28+84*I*sqrt(3))
cos(52,5°)= 1/4*(sqrt(3)*sqrt(2+sqrt(2))-sqrt(2-sqrt(2)))
cos(54°) = 1/4*sqrt(2)*sqrt(5-sqrt(5))
cos(57°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)+2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
cos(58,5°)= 1/8*(-sqrt(2)*sqrt(2-sqrt(2))*sqrt(5-sqrt(5))+(sqrt(5)+1)*sqrt(2+sqrt(2)))
cos(60°) = 1/2
cos(63°) = 1/8*(-sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
cos(66°) = 1/8*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
cos(67,5°)= 1/2*sqrt(2-sqrt(2))
cos(69°) = 1/16*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
cos(72°) = (-1+sqrt(5))/4
cos(75°) = 1/4*sqrt(2)*(sqrt(3)-1)
cos(76,5°)= 1/8*(sqrt(2)*sqrt(2+sqrt(2))*sqrt(5-sqrt(5))-(sqrt(5)+1)*sqrt(2-sqrt(2)))
cos(78°) = 1/8*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
cos(81°) = 1/8*(sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))
cos(82,5°)= 1/4*(-sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2)))
cos(84°) = 1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
cos(85,5°)= 1/8*(sqrt(2)*sqrt(2-sqrt(2))*sqrt(5+sqrt(5))-(sqrt(5)-1)*sqrt(2+sqrt(2)))
cos(87°) = 1/16*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
cos(90°) = 0

tan(0°) = 0
tan(6°) = 1/2*(sqrt(2)*sqrt(5-sqrt(5))-sqrt(3)*(sqrt(5)-1))
tan(7,5°) = sqrt(2)-sqrt(3)+sqrt(6)-2
tan(9°) = 1/4*(-sqrt(2)*(sqrt(5)+1)*sqrt(5+sqrt(5))+4*(sqrt(5)+1))
tan(15°) = 2-sqrt(3)
tan(18°) =sqrt(1-2/5*sqrt(5))
tan(22,5°)= sqrt(2)-1
tan(27°) = 1/4*(-sqrt(2)*(sqrt(5)-1)*sqrt(5-sqrt(5))+4*(sqrt(5)-1))
tan(30°) = 1/3*sqrt(3)
tan(36°) =sqrt(5-2*sqrt(5))
tan(37,5°)= -sqrt(2)+sqrt(3)+sqrt(6)-2
tan(42°) = 1/2*(-sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)+1))
tan(45°) = 1
tan(52,5°)= -sqrt(2)-sqrt(3)+sqrt(6)+2
tan(54°) = sqrt(1+2/5*sqrt(5))
tan(60°) = sqrt(3)
tan(63°) = 1/4*(sqrt(2)*(sqrt(5)-1)*sqrt(5-sqrt(5))+4*(sqrt(5)-1))
tan(66°) = 1/2*(sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)-1))
tan(67,5°)= 1+sqrt(2)
tan(72°) = sqrt(5+2*sqrt(5))
tan(75°) = 2+sqrt(3)
tan(78°) = 1/2*(sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)+1))
tan(81°) = 1/4*(sqrt(2)*(sqrt(5)+1)*sqrt(5+sqrt(5))+4*(sqrt(5)+1))
tan(82,5°)= sqrt(2)+sqrt(3)+sqrt(6)+2

Weitere Tangenswerte sind von komplizierterer Natur. Zum Beispiel
tan(3°) = (1-cos(6°))/sin(6°). Mit rationalem Nenner:
tan(3°) = -1/256*(-8+sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*sqrt(5)+sqrt(3)) *(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))+sqrt(5)+1) *(24+8*sqrt(5))
oder ausmultipliziert:
tan(3°) = 2 +sqrt(5) -3/2*sqrt(3) -1/2*sqrt(3)*sqrt(5) -sqrt(2)*sqrt(5-sqrt(5)) +3/4*sqrt(2)*sqrt(3)*sqrt(5-sqrt(5)) -1/2*sqrt(2)*sqrt(5-sqrt(5))*sqrt(5) +1/4*sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))*sqrt(5)

Wie beweist man eine solche Formel? Ich will es exemplarisch am folgenden Beispiel zeigen:
sin(7,5°)=1/4*(-sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2)))
Setzten wir voraus, es sei cos(15°)=sqrt(2)*(sqrt(3)+1)/4 bereits bewiesen
dann folgt mit der Formel für den halben Winkel
sin(7,5°)=sqrt(1/2*(1-cos(15°)) = sqrt(1/2*(1-sqrt(2)*(sqrt(3)+1)/4 )).
Wir müssen also noch nachweisen, dass a=b gilt für
a=1/4*(-sqrt(3)*sqrt(2-sqrt(2))+sqrt(2+sqrt(2))) und
b=sqrt(1/2*(1-sqrt(2)*(sqrt(3)+1)/4 )).

Dies kann man zeigen, indem man Wurzeln isoliert und quadriert. Man erhält dann für beide Terme, dass sie Lösungen der Gleichung 256*x^8-512*x^6+320*x^4-64*x^2+1=0 sind.

Eleganter ist folgendes Vorgehen:
a = 1/4 · (-sqrt(3)·sqrt(2-sqrt(2)) + sqrt(2+sqrt(2))) | ·4
4·a = -sqrt(3)·sqrt(2-sqrt(2)) + sqrt(2+sqrt(2)) | hoch 2
16·a² = 3·(2-sqrt(2)) + (2+sqrt(2)) - 2·sqrt(3)·sqrt(4-2)
= 6 - 3·sqrt(2) + 2 + sqrt(2) - 2·sqrt(6)
= 8 - 2·sqrt(2) - 2·sqrt(6)
b = 1/4 · sqrt (8 - 2·sqrt(2)·(sqrt(3) + 1))) | ·4
4·b = sqrt (8 - 2·sqrt(2) - 2·sqrt(6)) | ^2

16·b² = 8 - 2·sqrt(2) - 2·sqrt(6)
Somit: a² = b²

Es bleiben nur noch die Vorzeichen von a und b abzuschätzen.
Offensichtlich ist b positiv. Für a genügt es, die inneren Wurzeln auf 1 zu verkleinern:
4·a = -sqrt(3)·sqrt(2-sqrt(2)) + sqrt(2+sqrt(2))〉-sqrt(3)·sqrt(2-1) + sqrt(2+1) = 0
(Gerd Thieme)

Alle aufgelisteten Werte sind algebraisch, d.h. Nullstellen von Polynomen mit ganzzahligen Werten.
Einige Beispiele:

x                           ... ist Lösung der Gleichung
cos(45°)   sin(45°)         2x^2-1=0
cos(60°)   sin(30°)           2x-1=0
cos(30°)   sin(60°)           4x^2-3=0
cos(36°)   sin(54°)           4x^2-2x-1=0
cos(72°)   sin(18°)           4x^2+2x-1=0
cos(12°)   sin(78°)           16x^4+8x^3-16x^2-8x+1=0
cos(15°)   sin(75°)           16x^4-16x^2+1=0
cos(18°)   sin(72°)           16x^4-20x^2+5=0
cos(22,5°) sin(67,5°)         8x^4-8x^2+1=0
cos(24°)   sin(66°)           16x^4-8x^3-16x^2+8x+1=0
cos(48°)   sin(42°)           16x^4-8x^3-16x^2+8x+1=0
cos(54°)   sin(36°)           16x^4-20x^2+5=0
cos(67,5°) sin(22,5°)         8x^4-8x^2+1=0
cos(75°)   sin(15°)           16x^4-16x^2+1=0
cos(84°)   sin(6°)            16x^4+8x^3-16x^2-8x+1=0
tan(45°)           x-1=0
tan(15°)           x^2-4*x+1=0
tan(22,5°)         x^2+2*x-1
tan(30°)           3x^2-1=0
tan(60°)           x^2-3=0
tan(67,5°)         x^2-2x-1=0
tan(75°)           x^2-4x+1=0
tan(7,5°)          x^4+8x^3+2x^2-8x+1=0
tan(9°)            x^4-4x^3-14x^2-4x+1=0
tan(18°)           5x^4-10x^2+1=0
tan(27°)           x^4+4x^3-14x^2+4x+1=0
tan(36°)           x^4-10*x^2+5=0
tan(37,5°)         x^4+8x^3+2x^2-8x+1=0
tan(52,5°)         x^4-8x^3+2x^2+8x+1=0
tan(54°)           5*x^4-10*x^2+1=0
tan(72°)           x^4-10*x^2+5=0

Viele Werte lassen sich - ausgehend von den natürlichen Zahlen - nicht mit den vier Grundrechenarten und der Quadratwurzel berechnen, sind aber noch algebraisch, d. h. sie lassen sich als Nullstelle eines Polynoms darstellen. Zum Beispiel:
x... ... ist/sind Lösung(en) der Gleichung

cos(20°)=sin(70°) 8x^3-6x-1=0
cos(40°)=sin(50°)und cos(80°)=sin(10°) 8x^3-6x+1=0
cos(180°·k/7) (k=1,3,5) 8x^3-4x^2-4x+1=0
cos(360°·k/7) (k=1,2,3) 8x^3+4x^2-4x-1=0
cos(180°·k/11) (k=1,3,5) 32x^5-16x^4-32x^3+12x^2+6x-1=0
cos(360°·k/11) (k=1,2,3,4,5) 32x^5+16x^4-32x^3-12x^2+6x+1=0
cos(180°·k/13) (k=1,3,5) 64x^6-32x^5-80x^4+32x^3+24x^2-6x-1=0
cos(360°·k/13) (k=1,2,3,4,5,6) 64x^6+32x^5-80x^4-32x^3+24x^2+6x-1=0
cos(10°)=sin(80°) 64x^6-96x^4+36x^2-3=0
cos(50°)=sin(40°) 64x^6-96x^4+36x^2-3=0
cos(70°)=sin(20°) 64x^6-96x^4+36x^2-3=0
tan(10°), tan(50°) und tan(70°) 3x^6-27x^4+33x^2-1=0
tan(20°) tan(40°) x^6-33*x^4+27*x^2-3=0

Exemplarischer Beweis für x=sin(10°):

Mit sin³ α = ¹/₄(3·sinα - sin3α) folgt:
8x³-6x+1 =2(3·sin10°-sin30°)³-6sin10°+1 = 0, da 2sin30° = 1.

Exemplarischer Beweis für x=cos(360°/7):

Mit cos(2α) = 2cos² α - 1 und cos(3α) = 4cos³ α - 3 cosα folgt für x = cosα
cosα+cos(2α)+cos(3α) = x+2x²-1+4x³-3x = 4x³+2x²-2x-1
Für α = 360°/7 ist cosα+cos(2α)+cos(3α) =-¹/₂ (*)
und somit gilt für x = cos(^360°/₇)
die Gleichung 4x³+2x²-2x-1 =-¹/₂
oder 8x³+4x²-4x-1 =0
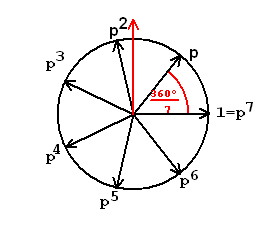
Die 7. Einheitswurzeln

Beweis von (*) (Beitrag in de.sci.mathematik
von Thomas Nordhaus und Wolfgang Kirschenhofer Februar 2008)


       360°                  iα            7
für α= ——— und p = cis(α) = e   folgt mit p = 1
        7
                                  7

         2   3   4   5   6   1 - p
1 + p + p + p + p + p + p  = —————  = 0
                             1 - p

Aus Symmetriegründen sind die Realteile von

       6    2     5            4      3
p und p  , p und p  sowie von p  und p  gleich und somit ist

                2        3        3        2
1 + Re(p) + Re(p ) + Re(p ) + Re(p ) + Re(p ) + Re(p) = 0

1 + 2cosα + 2cos(2α) + 2cos(3α) = 0

                                1
=> cosα + cos(2α) + cos(3α) = - -
                                2

Im Komplexen kann man zum Beispiel cos(20°) als Summe von zwei dritten Wurzeln schreiben.
cos(20°)=cbrt(1/16)*(cbrt(1+i*sqrt(3))+cbrt(1-i*sqrt(3))),
wobei cbrt die 3. Wurzel bezeichne und noch genauer spezifiziert werden muss,
welche dritte Wurzel gemeint ist (Im Komplexen sind die Wurzeln mehrdeutig).

Mit der Bezeichnung cis(α)=cos(α)+i*sin(α) ist
1+i*sqrt(3)=2*cis(60°)
1-i*sqrt(3)=2*cis(-60°) und damit die dritte Wurzel
cbrt(1+i*sqrt(3))=cbrt(2)*cis(20°)
cbrt(1-i*sqrt(3))=cbrt(2)*cis(-20°)

Eine zweite dritte Wurzel von
1-i*sqrt(3)=cbrt(2)*cis(-20°)=2*cis(300°) wäre
cbrt(1-i*sqrt(3))=cbrt(2)*cis(100°). Diese ist nicht gemeint.

Siehe Konstruktion des Siebenecks

Patrick Reichert hat in seiner Facharbeit in Klasse 10 bewiesen:

Satz: Ist cos(x) algebraisch, dann auch cos(q·x) für rationales q.

Da zum Beispiel cos(90°)=0 algebraisch ist, ist damit gezeigt, dass auch cos(1°), cos(2°), cos(3°) u.s.w. algebraische Zahlen sind.

Ähnlich kann man zeigen, dass sin(1°), sin(2°), sin(3°), ... algebraische Zahlen sind.

Den Satz möchte ich exemplarisch an der Herleitung für ein passendes Polynom zeigen, für das x=cos(5°) Nullstelle ist.

Voraussetzung:

          4        2
cos4x=8cos x - 8cos x + 1. Folgerung aus der "Moivreschen Formel".

(Solch eine Gleichung cosnx=... ist für alle n=2,3,4,... möglich.)

                                   3
x=cos(20°) erfüllt die Gleichung 8x - 6x -1 = 0 (siehe oben).

Behauptung: Es gibt ein Polynom h so, dass x=cos(5°) 

            Lösung der Gleichung h(x)=0 ist.

                       4   2                 3
Beweis: Setze f(x) = 8x -8x + 1 und g(x) = 8x  - 6x - 1

Die Funktionen wurden so gewählt, 

dass cos(20°)=f(cos(5°)) und g(cos(20°)) = 0 ist. Folgerung:

für h(x) = g(f(x))

         12       10         8       6       4     2
 =  4096x - 12288x   + 13824x - 7168x + 1680x -144x +1 

                                 (Term unwichtig) gilt:


h(cos(5°)) = g(f(cos(5°))=g(cos(20°)) = 0.

Dieses Polynom 12. Grades hat genau die 12 Nullstellen ±sin(x) und ±cos(x)
für x=5°, 25°,35° ,55°, 65° und 85° Nach einem Hinweis von Patrick Reichert erwähne ich, dass ±sin(x) und ±cos(x) für
x=1°, 7° ,11° ,13°, 17°, 19°, 23°, 29°, 31°, 37°, 41°,43°, 47°, 49°, 53°, 59°, 61°, 67°, 71°, 73°, 77°, 79°, 83° und 89°
genau die 48 Nullstellen des folgenden Polynoms 48. Grades sind: 281474976710656*x^48 -3377699720527872*x^46 +18999560927969280*x^44 -66568831992070144*x^42 +162828875980603392*x^40 -295364007592722432*x^38 +411985976135516160*x^36 -452180272956309504*x^34 +396366279591591936*x^32 -280058255978266624*x^30 +160303703377575936*x^28 -74448984852135936*x^26 +28011510450094080*x^24 -8500299631165440*x^22 +2064791072931840*x^20 -397107008634880*x^18 +59570604933120*x^16-6832518856704*x^14+583456329728*x^12-35782471680*x^10 +1497954816*x^8 -39625728*x^6 +579456*x^4 -3456*x^2+1=0

Nebenbei bemerkt: Pi und damit auch 1°=Pi/180 ist transzendent, d.h. nicht algebraisch.

Und: Nach dem allgemeine Satz von Lindemann-Weierstraß ist auch sin(1) transzendent (1 im Bogenmaß).

sin(α)/sin(β)

Bei Berechnungen am Dreieck kommt man über den Sinussatz zu Formeln der Form sin(α)/sin(β)
Mit Hilfe dieser Berechnungen und weiterer trigonometrischer Beziehungen kann man dann folgende nützliche Gleichungen beweisen: sin(1°)/sin(2°)=(1/2)/sin(89°)
sin(1°)/(1/2)=sin(2°)/sin(89°)
sin(2°)/sin(4°)=(1/2)/sin(88°)
sin(2°)/(1/2)=sin(4°)/sin(88°)
sin(2°)/sin(89°)=sin(1°)/(1/2)
sin(3°)/sin(6°)=(1/2)/sin(87°)
sin(3°)/(1/2)=sin(6°)/sin(87°)=1/8*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
sin(4°)/sin(8°)=(1/2)/sin(86°)
sin(4°)/(1/2)=sin(8°)/sin(86°)
sin(4°)/sin(88°)=sin(2°)/(1/2)
sin(5°)/sin(10°)=(1/2)/sin(85°)
sin(5°)/(1/2)=sin(10°)/sin(85°)
sin(6°)/sin(12°)=sin(24°)/sin(54°) =(1/2)/sin(84°)

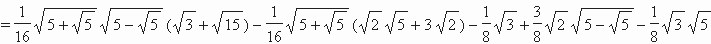
=1/16*sqrt(5+sqrt(5))*sqrt(5-sqrt(5))*(sqrt(3)+sqrt(15))
-1/16*sqrt(5+sqrt(5))*(sqrt(2)*sqrt(5)+3*sqrt(2))
-1/8*sqrt(3)+3/8*sqrt(2)*sqrt(5-sqrt(5))-1/8*sqrt(3)*sqrt(5)
sin(6°)/sin(18°)=sin(18°)/sin(66°)
sin(6°)/sin(24°)=sin(12°)/sin(54°)
sin(6°)/(1/2)=sin(12°)/sin(84°)=1/4*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
sin(6°)/sin(87°)=sin(3°)/(1/2) =1/8*(sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(5+sqrt(5)))
sin(7°)/sin(14°)=(1/2)/sin(83°)
sin(7°)/(1/2)=sin(14°)/sin(83°)
sin(8°)/sin(16°)=(1/2)/sin(82°)
sin(8°)/(1/2)=sin(16°)/sin(82°)
sin(8°)/sin(86°)=sin(4°)/(1/2)
sin(9°)/sin(12°)=sin(48°)/sin(81°)
sin(9°)/sin(18°)=(1/2)/sin(81°)
sin(9°)/(1/2)=sin(18°)/sin(81°) =1/4*(sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))
sin(9°)/sin(48°)=sin(12°)/sin(81°)
sin(10°)/sin(20°)=(1/2)/sin(80°)
sin(10°)/(1/2)=sin(20°)/sin(80°)
sin(10°)/sin(85°)=sin(5°)/(1/2)
sin(11°)/sin(22°)=(1/2)/sin(79°)
sin(11°)/(1/2)=sin(22°)/sin(79°)
sin(12°)/sin(18°)=(1/2)/sin(48°) =sin(42°)/sin(84°)
sin(12°)/sin(24°)=(1/2)/sin(78°)
sin(12°)/(1/2)=sin(18°)/sin(48°)=1/4*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
sin(12°)/(1/2)=sin(24°)/sin(78°)
sin(12°)/sin(42°)=sin(18°)/sin(84°)
sin(12°)/sin(54°)=sin(6°)/sin(24°)
sin(12°)/sin(81°)=sin(9°)/sin(48°)
sin(12°)/sin(84°)=sin(6°)/(1/2)=1/4*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
sin(13°)/sin(26°)=(1/2)/sin(77°)
sin(13°)/(1/2)=sin(26°)/sin(77°)
sin(14°)/sin(28°)=(1/2)/sin(76°)
sin(14°)/(1/2)=sin(28°)/sin(76°)
sin(14°)/sin(83°)=sin(7°)/(1/2)
sin(15°)/sin(18°)=sin(54°)/sin(75°)
sin(15°)/(1/2)=(1/2)/sin(75°)
sin(15°)/sin(54°)=sin(18°)/sin(75°)
sin(16°)/(1/2)=sin(32°)/sin(74°)
sin(16°)/sin(32°)=(1/2)/sin(74°)
sin(16°)/sin(82°)=sin(8°)/(1/2)
sin(17°)/(1/2)=sin(34°)/sin(73°)
sin(17°)/sin(34°)=(1/2)/sin(73°)
sin(18°)/sin(24°)=sin(48°)/sin(78°)
sin(18°)/(1/2)=(1/2)/sin(54°) =sin(36°)/sin(72°)
sin(18°)/sin(36°)=(1/2)/sin(72°) =sqrt(1/2-1/10*sqrt(5))
sin(18°)/sin(48°)=sin(12°)/(1/2)=sin(24°)/sin(78°) =1/4*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
sin(18°)/sin(66°)=sin(6°)/sin(18°)
sin(18°)/sin(75°)=sin(15°)/sin(54°)
sin(18°)/sin(81°)=sin(9°)/(1/2)=1/4*(sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))
sin(18°)/sin(84°)=sin(12°)/sin(42°)
sin(19°)/(1/2)=sin(38°)/sin(71°)
sin(19°)/sin(38°)=(1/2)/sin(71°)
sin(20°)/(1/2)=sin(40°)/sin(70°)
sin(20°)/sin(40°)=(1/2)/sin(70°)
sin(20°)/sin(80°)=sin(10°)/(1/2)
sin(21°)/(1/2)=sin(42°)/sin(69°) =1/8*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
sin(21°)/sin(42°)=(1/2)/sin(69°)
sin(22°)/(1/2)=sin(44°)/sin(68°)
sin(22°)/sin(44°)=(1/2)/sin(68°)
sin(22°)/sin(79°)=sin(11°)/(1/2)
sin(23°)/(1/2)=sin(46°)/sin(67°)
sin(23°)/sin(46°)=(1/2)/sin(67°)
sin(24°)/sin(27°)=sin(63°)/sin(84°)
sin(24°)/(1/2)=sin(48°)/sin(66°)=sin(54°)/sin(84°) =1/4*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(24°)/sin(48°)=(1/2)/sin(66°)
sin(24°)/sin(54°)=sin(6°)/sin(12°) =(1/2)/sin(84°)
sin(24°)/sin(63°)=sin(27°)/sin(84°)
sin(24°)/sin(78°)=sin(12°)/(1/2)=sin(18°)/sin(48°) =1/4*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
sin(25°)/(1/2)=sin(50°)/sin(65°)
sin(25°)/sin(50°)=(1/2)/sin(65°)
sin(26°)/(1/2)=sin(52°)/sin(64°)
sin(26°)/sin(52°)=(1/2)/sin(64°)
sin(26°)/sin(77°)=sin(13°)/(1/2)
sin(27°)/(1/2)=sin(54°)/sin(63°) =1/4*(-sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
sin(27°)/sin(54°)=(1/2)/sin(63°)
sin(27°)/sin(84°)=sin(24°)/sin(63°)
sin(28°)/(1/2)=sin(56°)/sin(62°)
sin(28°)/sin(56°)=(1/2)/sin(62°)
sin(28°)/sin(76°)=sin(14°)/(1/2)
sin(29°)/(1/2)=sin(58°)/sin(61°)
sin(29°)/sin(58°)=(1/2)/sin(61°)
(1/2)/sin(31°)=sin(59°)/sin(62°)
(1/2)/sin(32°)=sin(58°)/sin(64°)
(1/2)/sin(33°)=sin(57°)/sin(66°)
(1/2)/sin(34°)=sin(56°)/sin(68°)
(1/2)/sin(35°)=sin(55°)/sin(70°)
(1/2)/sin(36°)=sin(54°)/sin(72°) =sqrt(1/2+1/10*sqrt(5))
(1/2)/sin(37°)=sin(53°)/sin(74°)
(1/2)/sin(38°)=sin(52°)/sin(76°)
(1/2)/sin(39°)=sin(51°)/sin(78°)
(1/2)/sin(40°)=sin(50°)/sin(80°)
(1/2)/sin(41°)=sin(49°)/sin(82°)
(1/2)/sin(42°)=sin(48°)/sin(84°)
(1/2)/sin(43°)=sin(47°)/sin(86°)
(1/2)/sin(44°)=sin(46°)/sin(88°)
(1/2)/sin(46°)=sin(44°)/sin(88°)
(1/2)/sin(47°)=sin(43°)/sin(86°)
(1/2)/sin(48°)=sin(12°)/sin(18°) =sin(42°)/sin(84°)
(1/2)/sin(49°)=sin(41°)/sin(82°)
(1/2)/sin(50°)=sin(40°)/sin(80°)
(1/2)/sin(51°)=sin(39°)/sin(78°)
(1/2)/sin(52°)=sin(38°)/sin(76°)
(1/2)/sin(53°)=sin(37°)/sin(74°)
(1/2)/sin(54°)=sin(18°)/(1/2)
(1/2)/sin(54°)=sin(36°)/sin(72°)
(1/2)/sin(55°)=sin(35°)/sin(70°)
(1/2)/sin(56°)=sin(34°)/sin(68°)
(1/2)/sin(57°)=sin(33°)/sin(66°)
(1/2)/sin(58°)=sin(32°)/sin(64°)
(1/2)/sin(59°)=sin(31°)/sin(62°)
(1/2)/sin(61°)=sin(29°)/sin(58°)
(1/2)/sin(62°)=sin(28°)/sin(56°)
(1/2)/sin(63°)=sin(27°)/sin(54°)
(1/2)/sin(64°)=sin(26°)/sin(52°)
(1/2)/sin(65°)=sin(25°)/sin(50°)
(1/2)/sin(66°)=sin(24°)/sin(48°)
(1/2)/sin(67°)=sin(23°)/sin(46°)
(1/2)/sin(68°)=sin(22°)/sin(44°)
(1/2)/sin(69°)=sin(21°)/sin(42°)
(1/2)/sin(70°)=sin(20°)/sin(40°)
(1/2)/sin(71°)=sin(19°)/sin(38°)
(1/2)/sin(72°)=sin(18°)/sin(36°) =sqrt(1/2-1/10*sqrt(5))
(1/2)/sin(73°)=sin(17°)/sin(34°)
(1/2)/sin(74°)=sin(16°)/sin(32°)
(1/2)/sin(75°)=sin(15°)/(1/2)
(1/2)/sin(76°)=sin(14°)/sin(28°)
(1/2)/sin(77°)=sin(13°)/sin(26°)
(1/2)/sin(78°)=sin(12°)/sin(24°)
(1/2)/sin(79°)=sin(11°)/sin(22°)
(1/2)/sin(80°)=sin(10°)/sin(20°)
(1/2)/sin(81°)=sin(9°)/sin(18°)
(1/2)/sin(82°)=sin(8°)/sin(16°)
(1/2)/sin(83°)=sin(7°)/sin(14°)
(1/2)/sin(84°)=sin(6°)/sin(12°) =sin(24°)/sin(54°)
(1/2)/sin(85°)=sin(5°)/sin(10°)
(1/2)/sin(86°)=sin(4°)/sin(8°)
(1/2)/sin(87°)=sin(3°)/sin(6°)
(1/2)/sin(88°)=sin(2°)/sin(4°)
(1/2)/sin(89°)=sin(1°)/sin(2°)
sin(31°)/sin(62°)=(1/2)/sin(59°)
sin(32°)/sin(64°)=(1/2)/sin(58°)
sin(32°)/sin(74°)=sin(16°)/(1/2)
sin(33°)/sin(66°)=(1/2)/sin(57°)
sin(34°)/sin(68°)=(1/2)/sin(56°)
sin(34°)/sin(73°)=sin(17°)/(1/2)
sin(35°)/sin(70°)=(1/2)/sin(55°)
sin(36°)/sin(72°)=sin(18°)/(1/2) =(1/2)/sin(54°)
sin(37°)/sin(74°)=(1/2)/sin(53°)
sin(38°)/sin(71°)=sin(19°)/(1/2)
sin(38°)/sin(76°)=(1/2)/sin(52°)
sin(39°)/sin(78°)=(1/2)/sin(51°)
sin(40°)/sin(70°)=sin(20°)/(1/2)
sin(40°)/sin(80°)=(1/2)/sin(50°)
sin(41°)/sin(82°)=(1/2)/sin(49°)
sin(42°)/sin(54°)=sin(54°)/sin(78°)
sin(42°)/sin(69°)=sin(21°)/(1/2) =1/8*(-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))
sin(42°)/sin(84°)=sin(12°)/sin(18°)
sin(42°)/sin(84°)=(1/2)/sin(48°)
sin(43°)/sin(86°)=(1/2)/sin(47°)
sin(44°)/sin(68°)=sin(22°)/(1/2)
sin(44°)/sin(88°)=(1/2)/sin(46°)
sin(46°)/sin(67°)=sin(23°)/(1/2)
sin(46°)/sin(88°)=(1/2)/sin(44°)
sin(47°)/sin(86°)=(1/2)/sin(43°)
sin(48°)/sin(54°)=sin(66°)/sin(84°)
sin(48°)/sin(66°)=sin(24°)/(1/2)=sin(54°)/sin(84°) =1/4*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(48°)/sin(78°)=sin(18°)/sin(24°)
sin(48°)/sin(81°)=sin(9°)/sin(12°)
sin(48°)/sin(84°)=(1/2)/sin(42°)
sin(49°)/sin(82°)=(1/2)/sin(41°)
sin(50°)/sin(65°)=sin(25°)/(1/2)
sin(50°)/sin(80°)=(1/2)/sin(40°)
sin(51°)/sin(78°)=(1/2)/sin(39°)
sin(52°)/sin(64°)=sin(26°)/(1/2)
sin(52°)/sin(76°)=(1/2)/sin(38°)
sin(53°)/sin(74°)=(1/2)/sin(37°)
sin(54°)/sin(63°)=sin(27°)/(1/2) =1/4*(-sqrt(2)*(sqrt(5)-1)+2*sqrt(5+sqrt(5)))
sin(54°)/sin(72°)=(1/2)/sin(36°) =sqrt(1/2+1/10*sqrt(5))
sin(54°)/sin(75°)=sin(15°)/sin(18°)
sin(54°)/sin(78°)=sin(42°)/sin(54°)
sin(54°)/sin(84°)=sin(24°)/(1/2) =sin(48°)/sin(66°) =1/4*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(55°)/sin(70°)=(1/2)/sin(35°)
sin(56°)/sin(62°)=sin(28°)/(1/2)
sin(56°)/sin(68°)=(1/2)/sin(34°)
sin(57°)/sin(66°)=(1/2)/sin(33°)
sin(58°)/sin(61°)=sin(29°)/(1/2)
sin(58°)/sin(64°)=(1/2)/sin(32°)
sin(59°)/sin(62°)=(1/2)/sin(31°)
sin(63°)/sin(84°)=sin(24°)/sin(27°)
sin(66°)/sin(84°)=sin(48°)/sin(54°)
Weitere interessante Beziehungen sind sin(3°)*sin(87°)=1/16*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))
sin(6°)*sin(66°)=3/8-1/8*sqrt(5)
sin(6°)*sin(84°)=1/16*(sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))
sin(9°)*sin(81°)=1/8*sqrt(5)-1/8
sin(12°)*sin(48°)=1/8*sqrt(5)-1/8
sin(12°)*sin(78°)=1/16*(-sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(15°)*sin(45°)=1/4*sqrt(3)-1/4
sin(15°)*sin(60°)=3/8*sqrt(2)-1/8*sqrt(6)
sin(15°)*sin(75°)=1/4
sin(18°)*sin(36°)=sqrt(5/16-1/8*sqrt(5))
sin(18°)*sin(45°)=1/8*sqrt(10)-1/8*sqrt(2)
sin(18°)*sin(54°)=1/4
sin(18°)*sin(60°)=1/8*sqrt(15)-1/8*sqrt(3)
sin(18°)*sin(72°)=sqrt(5/32-1/32*sqrt(5))
sin(21°)*sin(69°) =1/16*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1))
sin(24°)*sin(66°) =1/16*(sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)-1))
sin(24°)*sin(84°)=1/8+1/8*sqrt(5)
sin(27°)*sin(63°)=1/8+1/8*sqrt(5)
sin(33°)*sin(57°) =1/16*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))+(sqrt(5)+1))
sin(36°)*sin(45°)=sqrt(5/16-1/16*sqrt(5))
sin(36°)*sin(54°)=sqrt(1/32*sqrt(5)+5/32)
sin(36°)*sin(72°)=1/4*sqrt(5)
sin(39°)*sin(51°) =1/16*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+(sqrt(5)-1))
sin(42°)*sin(48°) =1/16*(sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))
sin(42°)*sin(78°)=1/8*sqrt(5)+3/8
sin(45°)*sin(54°)=1/8*sqrt(2)+1/8*sqrt(10)
sin(45°)*sin(60°)=1/4*sqrt(6)
sin(45°)*sin(72°)=sqrt(1/16*sqrt(5)+5/16)
sin(45°)*sin(75°)=1/4+1/4*sqrt(3)
sin(54°)*sin(60°)=1/8*sqrt(3)+1/8*sqrt(15)
sin(54°)*sin(72°)=sqrt(1/8*sqrt(5)+5/16)
sin(60°)*sin(75°)=1/8*sqrt(6)+3/8*sqrt(2)
sin(6°)*cos(24°)=3/8-1/8*sqrt(5)
sin(12°)*cos(42°)=1/8*sqrt(5)-1/8
sin(15°)*cos(30°)=3/8*sqrt(2)-1/8*sqrt(6)
sin(15°)*cos(45°)=1/4*sqrt(3)-1/4
sin(15°)*cos(75°)=1/2-1/4*sqrt(3)
sin(18°)*cos(30°)=1/8*sqrt(15)-1/8*sqrt(3)
sin(18°)*cos(36°)=1/4
sin(18°)*cos(45°)=1/8*sqrt(10)-1/8*sqrt(2)
sin(18°)*cos(54°)=sqrt(5/16-1/8*sqrt(5))
sin(18°)*cos(72°)=3/8-1/8*sqrt(5)
sin(36°)*cos(45°)=sqrt(5/16-1/16*sqrt(5))
sin(36°)*cos(54°)=5/8-1/8*sqrt(5)
sin(36°)*cos(72°)=sqrt(5/16-1/8*sqrt(5))
sin(45°)*cos(54°)=sqrt(5/16-1/16*sqrt(5))
sin(45°)*cos(72°)=1/8*sqrt(10)-1/8*sqrt(2)
sin(45°)*cos(75°)=1/4*sqrt(3)-1/4
sin(48°)*cos(78°)=1/8*sqrt(5)-1/8
sin(54°)*cos(72°)=1/4
sin(60°)*cos(72°)=1/8*sqrt(15)-1/8*sqrt(3)
sin(60°)*cos(75°)=3/8*sqrt(2)-1/8*sqrt(6)
sin(66°)*cos(84°)=3/8-1/8*sqrt(5)