Siehe auch hier

Bemerkung: Die folgenden Zeichnungen wurden mit angefertigt.

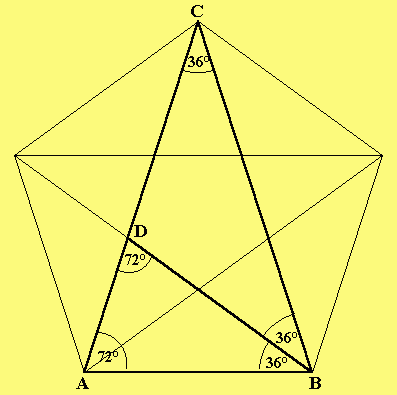
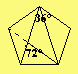
Wenn Du ein regelmäßiges Fünfeck mitsamt den Diagonalen zeichnest, so erhältst Du das 36°-72°-72°-Dreieck ABC (Beweis siehe nächste Figur). In diesem Dreieck schneidet die Winkelhalbierende des 72°-Winkels die gegenüberliegende Seite im goldenen Schnitt.Anders ausgedrückt:

D teilt die Strecke AC stetig, d.h. D teilt AC so, dass CA:CD = CD:DA ist. (Das Längenverhältnis ganze Strecke zur längeren Strecke ist dasselbe wie längere Strecke zur kürzeren Strecke.) Für den Beweis verwenden wir für die ähnlichen Dreiecke ABC und DAB die folgende Sätze:

• Zwei Dreiecke mit gleichen Winkeln sind ähnlich.(Eine hinreichende Bedingung.)
• In zwei ähnlichen Dreiecken verhalten sich entsprechende Seiten gleich.(Notwendige Bedingung.)

(Weiter übernächste Figur.)
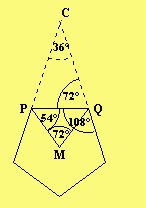Zunächst müssen wir noch zeigen, dass ABC ein 36°-72°-72°-Dreieck ist Das folgt sofort aus der Tatsache, dass die Innenwinkel eines Fünfecks 108° sind (Formel (n-2)·180°/n für n=5).

Ausführlicher: Fangen wir an mit dem Mittelpunktswinkel QMP bei M des regelmäßigen Fünfecks: Dieser beträgt 360°/5 = 72°.

Die restlichen Winkel können wir stets nach dem gleichen Schema berechnen: Ist ein Winkel in einem gleichschenkligen Dreieck bekannt, so sind die beiden anderen wegen der Winkelsumme von 180° berechenbar.

Die Innenwinkel des Dreiecks MPQ bei P und Q betragen(180° -  72°)/2 = 54°. Damit ist der Innenwinkel des Fünfecks bei Q 2·54° = 108°. Der zweite, der Nebenwinkel bei Q, ist 180° -108° = 72° und der Winkel bei C beträgt 180° - 2·72° = 36°. Aus der vorangegangenen Figur ergibt sich, dass die Winkel bei A und B(180°-36°)/2 = 72° weit sind.
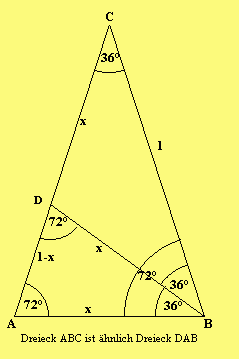Jetzt betrachten wir in den ähnlichen Dreiecken ABC und DAB das Verhältnis der Seiten, die einem Winkel von 72° und dem Winkel von 36° gegenüberliegen. Im Dreieck ABC ist das BC:AB, im Dreieck ABD ist das AB:AD. Also gilt:    BC:AB = AB:AD     oder, indem man gleiche Seiten ersetzt,    AC:CD = CD:AD. Somit teilt D die Strecke AC stetig.

Das Verhältnis wollen wir nun berechnen:

Nehmen wir an, die Seiten AC und BC haben im gleichschenkligen Dreieck ABC die Seitenlänge von einer Längeneinheit:    AC = BC = 1,
sowie AB, BD und DC haben im gleichschenkligen Dreieck ABD bzw. im gleichschenkligen Dreieck BDC die Länge x:    AB = BD = DC = x.

Das Verhältnis der Seiten, die einem Winkel von 72° und dem Winkel von 36° gegenüberliegen ist im Dreieck ABC 1:x und im Dreieck ABD entsprechend x:(1-x). Somit folgt:

    1    x         2
    - = ———— oder x  + x - 1 = 0
    x   1 -x

                          -
                        \/5 - 1
positive Lösung ist x = —————— ≈ 0,6180
                           2

Das Verhältnis des goldenen Schnitts kann man auch mit dem Kehrwert angegeben:

                    -         -
   1     2     2·(\/5+1)    \/5 + 1
   - = ————— = ————————— = ———————— ≈ 1,6180 
         -
   x   \/5-1     5 - 1        2

                                   1
Verwendet wird auch die Beziehung: - = 2·sin(54°) ≈ 1,6180
                                   x
                                                     1
An den Zahlenwerten sieht man gut die Beziehung  x = - - 1
                                                     x

Das Verhältnis des goldenen Schnitts ist irrational. Für die Pythagoreer (siehe unten) war dies ein großer Schock. Den Entdecker der Irrationalität sollen sie sogar ertränkt haben.

                           -
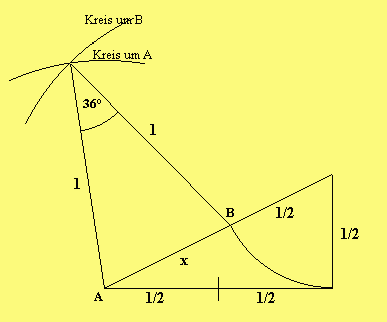
                         \/5 - 1
Kann man die Strecke x = ——————— konstruieren, 
                            2

kann man damit auch einen 36°-Winkel und das regelmäßigen Fünfeck zeichnen:

• Zeichne ein rechtwinkliges Dreieck mit den Seitenlängen 1 und 1/2!
  Die Hypotenuse hat die Länge
  

  
     —————————
    / 2     2   1  -
  \/ 1 + 0,5  = -\/5
                2
  
  

• Wie man nun x und den 36°-Winkel konstruiert, kannst Du der Zeichnung entnehmen.
• Wie Du schließlich mit dem 36°-Winkel ein regelmäßiges Fünfeck konstruieren kannst, siehst Du in der nächsten Figur

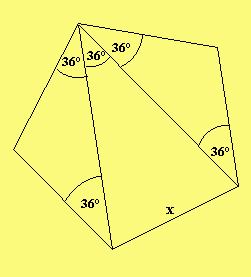
Konstruktion eines regelmäßigen Fünfecks

Wie Du den 36°-Winkel konstruieren kannst, wurde

an Hand der vorhergehenden Figur mit der

Konstruktion einer Strecke x der Länge

  -
\/5-1
————— erläutert.
  2

Durch Kopieren des 36°-Winkels an passenden Stellen erhältst Du nun ein regelmäßiges Fünfeck.

Du könntest stattdessen auch mit dem Mittelpunktswinkel von 36° ein regelmäßiges Zehneck konstruieren und in dieses ein regelmäßiges Fünfeck einzeichnen.
Siehe auch folgende Anleitung zur Konstruktion des Fünfecks

Im Faust hinderte der Drudenfuß Mephistopheles daran, das Studierzimmer zu verlassen:

MEPHISTOPHELES

Gesteh' ich's nur! Daß ich hinausspaziere
Verbietet mir ein kleines Hindernis,
Der Drudenfuß auf eurer Schwelle -


FAUST Das Pentagramma macht dir Pein?

Historische Bemerkung

Alle Diagonalen des regelmäßige Fünfecks bilden ein Sternfünfeck - als Pentagramm oder im Mittelalter als Drudenfuß bekannt.

Der Drudenfuß diente den Magiern als Schutz vor Dämonen: auf die Schwelle seiner Tür gezeichnet, sollte es dem Bösen den Eintritt ins Haus versperren.

Das Pentagramm war das Erkennungszeichen der Pythagoreer, Angehörige einer philosophisch-mathematischen Schule in der Antike, die die Konstruktion des Fünfecks mit Zirkel und Lineal, wie sie oben beschrieben wird, geheim hielten.

Lange Zeit war das Problem, welche Vielecke sich mit Zirkel und Lineal konstruieren lassen ungelöst. Erst Carl Friedrich Gauß (1777-1855) gelang die Konstruktion aller regelmäßiger n-Ecke, soweit möglich, nämlich außer dem Quadrat die regelmäßigen n-Ecke für n=3; 5; 17; 257; 65537; ... einschließlich aller möglichen Verdopplungen und Produkte.
Genauer: Gauß bewies, dass en reguläres n-Eck genau dann konstruierbar ist, wenn n das Produkt einer Zweierpotenz und von verschiedenen Fermatschen Primzahlen ist.

           k
         (2 )
Ist n = 2     + 1 Primzahl, so heißt diese Zahl Fermatsche Primzahl.

               0
             (2 )
Beispiele:  2    + 1 = 3  ist Primzahl: Das 3-Eck ist konstruierbar.

               1
             (2 )
             2    + 1 = 5  ist Primzahl: Das 5-Eck ist konstruierbar (siehe Überschrift).

               2
             (2 )
            2    + 1 = 17 ist Primzahl: Das 17-Eck ist kontruierbar.

               3
             (2 )
            2    + 1 = 257 ist Primzahl: Das 257-Eck ist kontruierbar.

               4
             (2 )
            2    + 1 = 65 537 ist Primzahl: Das 65 537-Eck ist kontruierbar.

               5
             (2 )
            2    + 1 = 4 294 967 297 = 641·6 700 417 ist keine Primzahl:

            Das 4 294 967 297-Eck ist nicht kontruierbar.

Nebenbei bemerkt:

Gauß hat nur bewiesen, dass das 65 537-Eck konstruierbar ist. Wie dies zu bewerkstelligen ist, kann man nachlesen in:
J. Hermes [in Lingen]: Uber die Teilung des Kreises in 65537 gleiche Teile.
Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen,
Math.-Phys.Klasse, Bd. 1894, Heft 3, S. 170-186
In diesem Artikel wird beschrieben, wie sie durchgeführt wird. Tatsächlich soll J. Hermes die Konstruktion auch vollbracht haben, wozu er anscheinend 10 Jahre brauchte. Zeitartikel

Angeblich gehört zur Institutsbibliothek des Mathematischen Instituts der Universität Göttingen eine Abteilung mit Koffern, wo die Nachlässe von Mathematikern verwahrt werden mit Schmierzetteln, die keiner versteht und keiner wegzuwerfen wagt. Da soll es auch einen Koffer von J. Hermes mit den Zeichnungen zu obiger Arbeit geben.

---

Literatur (sehr zu empfehlen!): Alfred S. Posamentier "119 Unterrichtseinheiten" Aus der Serie "Arbeitsmaterialien Mathematik" Ernst-Klett-Verlag Stuttgart, 1994. Einheit 68 "Das Goldene Dreieck".
Wikipedia, die freie Enzyklopädie

---