Joachim Mohr Mathematik Musik
Häufig gestellte Fragen und
Antworten zur Mathematik
- Häufig auftretende Fehler
- hilfreiche Floskeln.
- Kurzfassung.
- Potenzieren geht vor Punkt- und Strichrechnung, Punktrechnung geht vor Strichrechnung.
- Durch Differenzen und durch Summen kürzen nur die D...
- Bei Wurzeln die Noten purzeln.
-
Die Logarithmen und Potenzen sich wie Ebbe
und Flut ergänzen
Beispiel zum richtigen Logarithmieren - Ableitungen von 2x etc.
- Oberstufe I
- Frage zur Zwei-Punkteform
- Definitionsbereichen ber Verkettung zweier Funktionen
- Oberstufe II Analysis
- Symmetrie bei Schaubildern I
- Symmetrie bei Schaubildern II
- Was bedeutet stetige Ergänzung?
- Integral: Einfach genial
- Was ist der Unterschied zwischen stetigem Wachstum und diskretem Wachstum?
- Oberstufe II Geometrie
- Zur Vektorrechnung
- Ich soll einen Vektor durch andere darstellen. Wie mache ich das?
- Wer kann mir erklären was ich unter linearer (Un-)Abhängigkeit von Vektoren zu verstehen habe?
- Schwerpunktsatz
- Skalarprodukt
- Windschiefe Geraden
- Flächeninhalt eines Dreiecks
- Koordinaten des dritten Dreieckspunktes
- Wann liegen drei Punkte auf einer Geraden?
- Wann schneiden sich drei Geraden in einem Punkt?
- Wie berechnet man den Umkreismittelpunkt eines Dreiecks?
- Wie gibt man einen Kreisbogen durch drei Punkte an?
- Oberstufe Grundlagen
- Was bedeutet Koeffizientenvergleich (5 Beispiele aus der Vektorrechnung und der Analysis)
- Oberstufe III Analysis
- Nach wie vielen Jahren ist ein Darlehen getilgt?
- Zur Kettenregel
- Was ist die Ableitung von f(x)=2x, g(x)=xx, h(x)=21/x und i(x)=x1/x?
- Umkehrfunktion
- Höhere Mathematik im Reellen
- Warum ist arctan(tan(φ)) = φ für manche Werte von φ falsch?
- Wie löse ich die Gleichung x·ex=a nach x auf?
- Wann hat die Gleichung xy = y x eine weitere Lösung außer x=y?
- Mein Computer "sieht nicht", dass 1.333...33 der Bruch 4/3 ist. Wie kann ich ihm das beibringen?
- Affine Räume
- Neu: Affine Räume, Affinitäten, Ähnlichkeitsabbildungen und Kongruenzabbildungen
- Komplexe Zahlen
- Was ist hier falsch? -1 = sqrt(-1)·sqrt(-1) = sqrt((-1)·(-1)) = sqrt(1) = 1
- Wie löse ich die Gleichung x2=a+b·i?
- Numerik
- Warum berechnet Excel und mein Taschenrechner 9x4-y4+2y2 falsch?
- Warum berechnet mein Computer 0,1 + 0,9 falsch?
- Neu: Wie berechnet man die Ausgleichsgerade durch viele Punkte
- Allgemein
- Was ist ein Kettenbruch?
- Die Heron'sche Formel zur Dreiecksfläche
- Der Satz vom arithmetischen und geometrischen Mittel
- Der allgemeine Satz vom arithmetischen und geometrischen Mittel
- Wie berechne ich die Lösung einer Gleichung 3. oder 4. Grades zum Beispiel x3 - 2x + 4 = 0
- Berechnung des Flächeninhaltes eine Vierecks
- Warum ist tan(15°)=2 - sqrt(3)?
- Kann man cos(arctan(x)/2) und sin(arctan(x)/2) vereinfachen?
Alfred Heiligenbrunner meint
Siehe: hier...
| Dies ist von großer theoretischer und praktischer Bedeutung | Es interessiert mich |
| Das ist ein interessantes Analogon zu ... | Ich brauche irgendeine Rechtfertigung für die Publikation |
| Dies ist für die Anwendung interessant | Nichts für mich |
| Das Problem ist schwierig | Ich weiß die Antwort nicht |
| Das Problem ist leicht | Ich weiß die Antwort |
| Dieser Satz ist wohlbekannt | Ich finde das Literaturzitat nicht |
| Der Beweis von X ist genial | Ich verstehe ihn |
| Der Beweis von Y ist interessant | Ich verstehe ihn nicht |
| Der Beweis geschieht durch direktes Nachrechnen | Ich habe meine Unterlagen verloren |
| Wir bringen etwa diesen Teil des Beweises | Das ist der einzige Teil, den ich zusammenbringe |
| Die Details seien dem Leser überlassen | Ich bringe sie nicht zusammen |
| Der Rest ist trivial | Ich weiß nicht mehr weiter |
| Ohne Beschränkung der Allgemeinheit (o.B.d.A.) | Wir behandeln nur einen besonders leichten Fall |
| Der Leser wird bemerkt haben | Hoffentlich hat's niemand bemerkt |
| Man mag einwenden, dass ... | Ich werde den Einwand jetzt erheben, weil ich eine großartige Antwort darauf habe |
| Es wird noch viel Arbeit nötig sein, bis alle Fragen geklärt sind I | ch verstehe es nicht |
| Es gibt noch keine zusammenfassende Arbeit darüber | Auch die anderen verstehen es nicht |
| Es ist zu hoffen, dass diese Arbeit weitere Untersuchungen auf diesem Gebiet anregen wird | Diese Arbeit ist schwach, aber alle Arbeiten auf diesem blöden Gebiet sind es auch |
| Der Größenordnung nach richtig | Falsch |
| Objektiv | Nach meiner Ansicht |
| Subjektiv | Nach Ansicht der anderen |
|
The trick in teaching mathematics is that I do the easy
part and you do the hard part.
... eine treffliche Bemerkung von Hahn
Hiang-Shin in "Complex Numbers and Geometry"
|
|
Frage: Was ist ein Parameter? Antwort: Ein
Parameter ist eine variable Konstante :-)
(Folklore)
|
Häufig gemachte Fehler - Kurzfassung
| Potenzieren geht vor Punkt- und Strichrechnung Richtig: -24 = -(24) = -16 Falsch: -24 ist nicht (-2)4 = 16 |
Kürzen darf man nur Faktoren, d.h. wenn
Zähler und Nenner in ein Produkt zerlegt
wurden:
2ab 2b 2a + b 2 + b
I Richtig: ———— = —— (gekürzt mit a) Falsch: —————— ist nicht ————— !
3a 3 3a 3
|
Das Distributivgesetz gilt nur, wenn in der
Klammer eine Summe steht.
Richtig: 2(a+b) = 2a + 2b Richtig: 2(ab) = 2ab Falsch: 2(ab) ist nicht 2a·2b
|
Summen unter Wurzeln kann man im
Allgemeinen nicht vereinfachen:
—————— ——————
2 2 2 2
Richtig: \/a · b = a · b für a,b > 0 Falsch: \/a + b ist nicht a + b.
|
Logarithmen von Summen kann man im
Allgemeinen nicht vereinfachen:
2 3 2 3
Richtig: lg (10 · 10 ) = 2 + 3 Falsch: lg(10 + 10 ) ist nicht 2 + 3
2 3 2 3
Oberstufe: Richtig ln (e ·e ) = 2 + 3 Falsch: ln (e + e ) ist nicht 2 + 3
|
|
Ableitung von Exponentialfunktionen:
Die Ableitung von f(x) = 2x ist nicht x·2x-1 sondern f'(x) = ln2·2x. |
Potenzieren geht vor Punkt- und Strichrechnung, Punktrechnung geht vor Strichrechnung.
Bekannt ist die Klammerersparnisregel "Punkt- vor "Strichrechnung":Beispiel: 2·3 + 4·7 = (2·3) + (4·7) = 6 + 28 = 34
Entsprechend gilt die Klammerersparnisregel: "Potenzieren vor Punkt- und Strichrechnung".
Klar ist: 1 - 3·24 = 1 - 3·(24) = 1 - 3·16 = - 47
Manchmal vergißt man diese Regel jedoch bei Beispielen wie diesen:
-24 = - (24) = - 16 und nicht gleich (-2)4 = + 16
Durch Differenzen und durch Summen kürzen nur die Dummen
(Man verzeihe mir den Reim. Er stammt nicht
von mir. Unten wird gezeigt, wie man gescheit durch
Summen kürzt.)
2a + b 2 + b 2a + b 2 + b:a —————— ist nicht ————— sondern —————— = ——————— (keine Vereinfachung!) 3a 3 3a 3Kürzen heißt: Zähler und Nenner durch dieselbe Zahl dividieren. Der Wert ändert sich dabei nicht.
Beispiel:
2
35 5 2a 2a
—— = - (gekürzt mit 7) ——— = —— (gekürzt mit a)
49 7 3a 3
Steht im Zähler eine Summe zum Beispiel ac + bc, dann
muss bei Division durch eine Zahl jeder Summand durch diese Zahl
dividiert werden.(ac + bc): c = (ac):c + (bc):c = a + b. Dasselbe in Bruchschreibweise:
ac + bc (a+b)c a + b
——————— = —————— = ————— (gekürzt mit c) = a + b
c c 1
ac + bc a + b
Also ist zum Beispiel ——————— = ————— (gekürzt mit c).
5c 5
ac + bc (a + b)c a + b
Ausführlich: ——————— = ———————— = ————— (gekürzt mit c)
5c 5c 5
Weitere Beispiele:
2 2
2a + a 2 + a 2a + a a(2+a) 2 + a
—————— = —————. Ausführlich: ——————— = —————— = ——————
5a 5 5a 5a 5
b b
a(2 + -) 2 + -
2a + b a a
—————— = ———————— = ————— keine Vereinfachung! (Siehe Eingangsbeispiel.)
3a 3a 3
21a + 14b 3a + 2b 21a + 14b 7(3a+2b) 3a + 2b
————————— = ———————. Ausführlich ————————— = ———————— = ———————
7x - 35 x - 5 7x - 35 7(x-5) x - 5
Bei Wurzeln die Noten purzeln
——————
2 2
\/a + b ist nicht a + b. Richtig ist:
————— ————————————
2 2 2 2
\/a ·b = a·b oder \/a + 2ab + b = a + b (a,b ≥ 0)
- 2
Denn \/a = x bedeutet x = a (a, x ≥ 0).
—— ————
2 2
Beachte auch, dass \/a = |a| ist. Zum Beispiel \/(-3) = |-3| = 3
Das heißt: Was rechts der Wurzel steht, muss
quadriert das sein, was unter der Wurzel steht. Hier:
—————
2 2 2 2 2
\/a ·b = a·b, da (a·b) = a ·b und
————————————
2 2 2 2 2
\/a + 2ab + b = a + b, da (a + b) = a + 2ab + b .
——————
2 2
Deshalb kann man \/a + b nicht vereinfachen. Zum Beispiel ist:
———————
2 2 ——
\/3 + 4 = \/25 = 5 und nicht 3 + 4 = 7.
Die Logarithmen und Potenzen sich wie Ebbe und Flut ergänzen
Aufgabe: Löse 102x + 10x = 110Häufig begegnet man folgendem fundamentalen Fehler:
"Wenn man auf beiden Seiten den Logarithmus nimmt, erhält man:
2x x
lg10 + lg10 = lg110 (falsch!!! Siehe die Regeln unten im Kasten!!!)
1
also 2x + x = lg 110 und somit x = -lg110 = 0,6805"
3
x
Man löst vielmehr die Gleichung durch die Substitution v = 10 .
2x x 2
Dann wird aus 10 + 10 - 110 = 0 die quadratische Gleichung v + v - 110 = 0
x x
mit den Lösungen v = 10 = 10 und v = 10 = -11
1 2
x x
Aus 10 = 10 folgt x = 1. Die Gleichung 10 = -11 hat keine Lösung.
2x x
Somit ist x = 1 Lösung der Gleichung 10 + 10 = 110.
2 1
Probe: 10 + 10 = 110
Ableitung von Exponentialfunktionen (Oberstufe): Siehe Kettenregel und Exponentialfunktion
Lösungen der 5.Übung
Mittelstufe (zu Potenzen)
Frage: Was ist (-3)2 und -32?Antwort: Es gilt die Klammerersparnisregel: Zuerst Potenzieren, dann Punktrechung (Multiplizieren und Dividieren) und ganz zum Schluss Strichrechnung (Addieren und Subtrahieren). Klammerausdrücke werden jedoch als erstes ausgewertet.
(-3)2 bedeutet: Multipliziere (-3) mit sich selbst (2 mal).
Also (-3)2 = (-3)·(-3) = 9
-32 bedeutet: Potenziere zuerst 3 mit 2 und nimm davon den negativen Wert.
Also -32 = - (32) ("zuerst Potenzieren") = - 9.
Oberstufe
log(u+v) kann nicht zu logu + logv vereinfacht werden.Es wird häufig verwechselt mit log(u·v) = logu + logv
| Wichtige Regeln beim Logarithmieren und Potenzieren |
|---|
m+n m n
log(u·v) = log u + log v. Zum Vergleich: a = a ·a .
|
m
u m-n a
log - = log u - log v. Zum Vergleich: a = ———.
v m
a
|
z m·n m n
log u = z·log u. Zum Vergleich a = (a ) .
Insbesondere:
x
lg 10 = x, da lg 10 = 1 (lg = Logarithmus zur Basis 10)
x
ln e = x, da ln e = 1 (ln = natürlicher Logarithmus [Basis: e = 2,718...])
|
lg a ln a
log a = ———— = ———— ( log a = Logarithmus zur Basis b)
b lg b ln b b
|
|
Denn Logarithmen sind Exponenten: Was rechts des
Logarithmus steht, ist eine Potenz. Die Logarithmengesetze spiegeln deshalb die Potenzgesetze in die andere Richtung: Aus "·" wird "+", aus ":" wird "-" und aus "hoch" wird "·".
Beispiel mit 10-er Potenzen (lg = Logarithmus zur Basis 10)
u
lg 1000 = u bedeutet: 10 = 1000, also ist u = lg 1000 = 3.
v
lg 10000 = v bedeutet: 10 = 10000, also ist v = lg 10000 = 4.
x u v u+v
lg (1000·10000) = x bedeutet 10 = 1000·10000 = 10 ·10 = 10 => x = u + v.
Also: lg (1000·10000) = x = u + v = lg 1000 + lg 10000 = 3 + 4 = 7.
u
1000 y 1000 10 u - v
Ähnlich lg ————— = y bedeutet 10 = ————— = ———— = 10 => y = u - v.
10000 10000 v
10
1000
Also: lg ————— = y = u - v = lg 1000 - lg 10000 = 3 - 4 = -1
10000
25 z 25 u 25 25·u
Und: lg 1000 = z bedeutet 10 = 1000 = (10 ) = 10 => z = 25·u.
25 25 3 25 75
Also: lg 1000 = 25·u = 25·lg1000 = 25·3 = 75. Probe: 1000 = (10 ) = 10 .
|
| Wenn Du die Herleitung (Kasten über diesem) verinnerlicht hast, wirst Du nicht mehr in Versuchung kommen lg(u+v) mit lgu + lgv gleichzusetzen: lg(u + v) lässt sich so nicht umformen!. |
1000·10x = 700
und möchte diese nach x auflösen, so sieht man häufig folgende Umformung (lg = log zur Basis 10):
lg1000·lg10x = lg 700 (falsch!!).
Richtig (aber nicht die beste Umformung) ist:
lg1000 +lg10x = lg 700 => 3 + x = lg 700 => x = lg700 - 3
Folgende Umformung ist besser:
x x 7 7
1000·10 = 700 => 10 = —— => x = lg—— = lg 7 - lg 10 = lg 7 - 1
10 10
Man beachte: lg 700 = lg(7·100) = lg7 + lg100 = lg7 + 2.
Die Ergebnisse sind also gleich: lg700 - 3 = lg 7 - 1
Beispiel für das Rechnen mit Logarithmen:Bestimme das Alter eines Fossils, dessen gemessener C14-Anteil 1,4% des ursprünglichen Anteils ist! (Halbwertszeit von C14: 5730 Jahre.)
1. Lösung:
-kt
Ansatz: B(t) = A·e (B Bestand an C14, t: Jahre)
-5730k 1 -5730k 1
Aus B(0) = A und B(5730) = A·e = -·A folgt: e = -
2 2
1 ln2
=> -5730k = ln - = - ln2 => k = ———— ≈ 0,000121.
2 5730
Damit haben wir also k berechnet. Das Alter wird folgendermaßen bestimmt:
-kt -kt
B(t) = Ae = 1,4% von B(0) = 0,014·A => e = 0,014 => -kt = ln 0,014
ln0,014
Also t = - ————————·5730 = 35 288 [Jahre].
ln2
|
2. Lösung: (lb = Logarithmus zur Basis 2)
-kt
Ansatz: B(t) = A·2 (B Bestand an C14, t: Jahre)
-5730k 1 -5730k 1
Aus B(0) = A und B(5730) = A·2 = -·A folgt: 2 = -
2 2
1 1
=> -5730k = lb - = - 1 => k = ———— ≈ 0,000175.
2 5730
Damit haben wir also k berechnet.
t
- ————
5730 -1 A
Somit ist B(t) = A·2 . Man sieht sofort B(5730) = A·2 = -.
2
Das Alter wird folgendermaßen bestimmt:
-kt -kt
B(t) = A2 = 1,4% von B(0) = 0,014·A => 2 = 0,014 => -kt = lb 0,014
lg0,014
Also t = - lb 0,014·5730 = - ———————·5730 = 35 288 [Jahre]
lg2
|
lgx lnx lg0,014 ln0,014
Merke! logx = ——— = ——— Hier: lb0,014 = log 0,014 = ——————— = ———————
b lgb lgb 2 lg2 ln2
|
| Ergebnis: Das Fossil ist rund 35 Tausend Jahre alt. |
Frage zur
Zwei-Punkte-Form:
Warum berechnet man die Steigung einmal mit zwei bekannten
Punkten, das andere Mal mit nur einem Punkt und einem
allgemeinen Punkt P(x|y)?
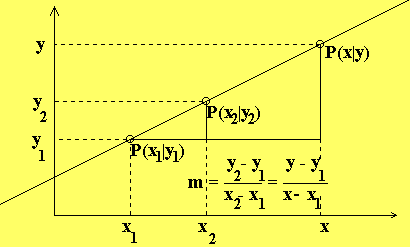
3 - 2 1
Beispiel: P (2|2) P (4|3) m = ————— = -
1 2 4 - 2 2
y - 2
P (2|2) P(x|y) m = —————
1 x - 2
Die Steigungen sind gleich:
y - 2 1 1
————— = - => y - 2 = -(x - 2)
x - 2 2 2
1
=> y = -x + 1
2
Antwort:
Du musst dich dabei fragen: Was bedeutet y = mx + c?
D.h. Wie kommt man von einer algebraischen Gleichung zur Geraden, einem geometrischen
Objekt?
Dieses Problem löste René Descartes durch folgende Überlegung:
| P(x|y) ist Punk der Geraden, wenn seine Koordinaten die Gleichung y = mx + c erfüllen. |
1
Etwa P(7|4,5) liegt auf der Geraden mit der Gleichung y = -x + 1
2
1
da "4,5 = -·7 + 1" wahr ist.
2
Und so ist auch die Zweipunkteform zu verstehen:
Der Punkt P(x|y) liegt auf der Geraden durch die zwei Punkte P (x |y )
1 1 1
y - y y - y
1 2 1
und P (x |y ), wenn x und y die Gleichung —————— = —————— erfüllt (x ≠ x , x ≠ x ).
2 2 2 x - x x - x 1 1 2
1 2 1
Im Beispiel: Der Punkt P(x|y) liegt auf der Geraden durch die zwei Punkte P (2|2)
1
y - 2 3 - 2
und P (4|3), wenn x und y die Gleichung —————— = ————— erfüllen (x ≠ 2).
2 x - 2 4 - 2
Die Bedingung x ≠ x kann man noch vermeiden:
1
Der Punkt P(x|y) liegt genau dann auf der Geraden (P (x |y )P (x |y )), wenn seine
1 1 1 2 2 2
y - y
2 1
Koordinaten die Gleichung y - y = ———————·(x - x ) erfüllen. (x ≠ x )
1 x - x 1 2 1
2 1
Sonderfall: x = x . (Dann muss bei verschiedenen Punkten y ≠ y sein.)
1 2 2 1
Die Gerade durch P und P hat dann die Gleichung x = x , d.h.
1 2 1
P(x|y) liegt genau dann auf der Geraden, wenn x = x (und y beliebig) ist.
Wie ermittle ich bei der Verkettung von Funktionen den Definitionsbereich
Antwort: Mit freundlcher Erlaubnis von Herr Ulrich Warnecke verweise ich auf seine schöne Darstellung:Verkettung von Funktionen
Symmetrische Schaubilder von Funktionen
I Symmetrie zur y-Achse und
II Symmetrie zum Ursprung
Wir beschäftigen uns hier mit zwei Fragestellungen,
die dasselbe Thema unter verschiedenen Gesichtspunkten
betrachtet:
- Wie erkenne ich am Funktionsterm, ob das Schaubild symmetrisch zur y-Achse oder zum Ursprung ist?
- Wenn ich weiß, dass das Schaubild symmetrisch ist, was kann ich dann über die Funktion sagen?
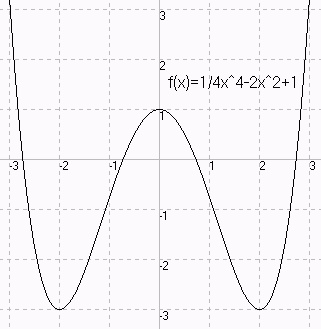
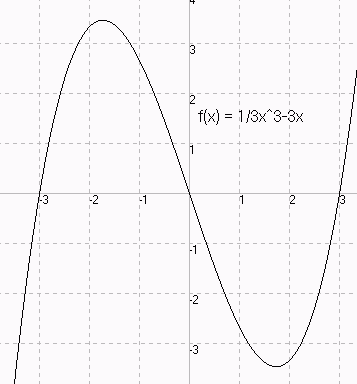
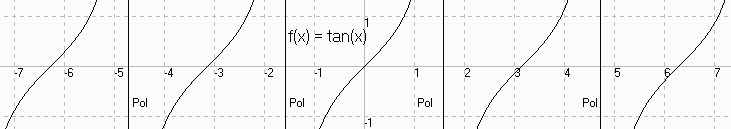
Wir sehen
symmetrisch zur y-Achse symmetrisch zum Ursprung
——————————————————————— ————————————————————————
1 4 2 1 3
f(x) = -x - 2x + 1 f(x) = -x - 3x
4 3
2
x 2x
f(x) = —————— f(x) = ——————
3 3
x + x x + x
(Dass die beiden Terme kürzbar sind, ist vorerst unerheblich)
f(x) = cos(x) f(x) = sin(x) und f(x) = tan(x)
Wir suchen nun ein Kriterium, bei dem wir dem Term schon
ansehen, ob das Schaubild symmetrisch zum Ursprung bzw. zur y-Achse
ist.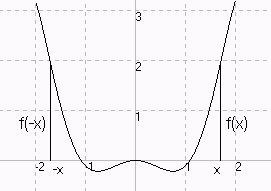
Das Schaubild von f ist symmetrisch zur y-Achse
<=>
Für alle x ε D : f(-x) = f(x)
f
Beispiele:
1 4 2 1 4 2 1 4 2
a) f(x) = -x - 2x + 1, x ε R. Es folgt: f(-x) = -(-x) - 2(-x) + 1 = -x - 2x + 1
4 4 4
2 2 4 4 6 6
da stets gilt (-x) = x , (-x) = x , (-x) = x ... (gerade Hochzahlen)
Somit ist f(-x) = f(x) für alle x ε R und das Schaubild symmetrisch zur y-Achse.
x -x x
b) f(x) = ————— x ε R\{0}. Es folgt: f(-x) = —————— = ————— = f(x)
3 3 3
x +x -x - x x + x
(Zähler und Nenner ändern beim Übergang von x zu -x das Vorzeichen.)
Also ist das Schaubild symmetrisch zur y-Achse.
1
Bemerkung: Die Funktion ist identisch mit g(x) = —————, x ε R,
2
x + 1
bis auf den Umstand dass g einen größeren Definitionsbereich hat.
(Aus psychologischen Gründen wurde ein Term mit ungeraden Hochzahlen gewählt.)
c) Umgekehrt: Weiß man, dass das Schaubild der Kosinusfunktion symmetrisch
zur y-Achse ist, kann man sofort schließen:
cos(-x) = cos(x) für alle x ε R
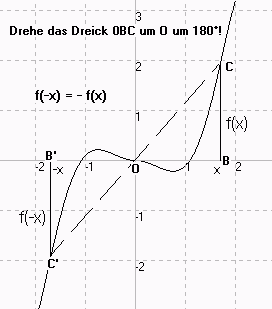
Das Schaubild von f ist symmetrisch zum Ursprung
<=>
Für alle x ε D : f(-x) = - f(x)
f
Beispiele:
1 3 1 3
a) f(x) = -x - 3x, x ε R. Es folgt: f(-x) = ——x + 3x = - f(-x)
3 3
3 3 5 5
da stets gilt (-x) = - x , (-x) = - x ... (ungerade Hochzahlen)
Also ist das Schaubild symmetrisch zum Ursprung.
2 2 2
2x 2x 2x
b) f(x) = ——————, x ε R\{0}. Es folgt: f(-x) = ——————— = - ————— = - f(x)
3 3 3
x + x - x - x x + x
(Der Nenner ändert sein Vorzeichen, der Zähler nicht.)
Also ist das Schaubild symmetrisch zum Ursprung.
2x
Bemerkung: Die Funktion ist identisch mit g(x) = —————
2
x + 1
bis auf den Umstand dass g einen größeren Definitionsbereich hat.
(Aus psychologischen Gründen wurde ein Term mit höheren Hochzahlen gewählt.)
c) Umgekehrt: Weiß man, dass das Schaubild der Sinus- und Tangensfunktion symmetrisch
zum Ursprung ist, kann man sofort schließen:
sin(-x) = - sin(x) und tan(-x) = -tan(x) für alle x ε R.
Symmetrische Schaubilder von Funktionen
III Symmetrie zu einer Parallelen der y-Achse und
IV Symmetrie zu einem Punkt
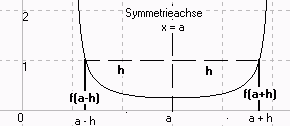
Das Schaubild von f ist symmetrisch zur Geraden x= a
<=>
Für alle x ε D : f(a - h) = f(a + h)
f
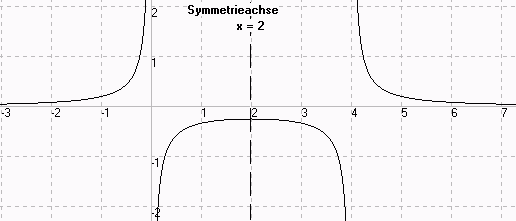
Beispiel:
1
f(x) = ——————
x(x-4)
symmetrisch zu
x = 2, denn
2
f(2+h)=——————————
(h+2)(h-2)
2
f(2-h)=———————————
(2-h)(-h-2)
= f(2+h)
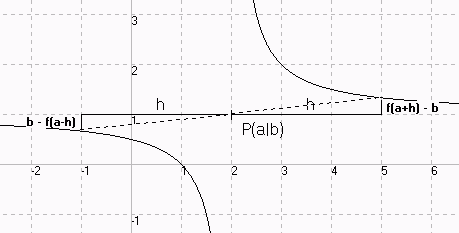
Das Schaubild von f ist
symmetrisch zur P(a|b)
<=>
Für alle x ε D :
f
b - f(a - h) = f(a + h) - b
oder (äquivalent)
f(a-h) + f(a+h)
——————————————— = b
2
(Mittelwert)
Beispiel:
x - 1
f(x) = ————— x ε R\{2} (Zeichnung siehe oben)
x - 2
Das Schaubild ist symmetrisch zum Punkt P(2|1), denn
1 - h 1 + h h - 1 1 + h
f(2-h) + f(2+h) = ————— + ————— = ————— + ————— = 2
-h h h h
f(2-h) + f(2+h)
Somit ist ——————————————— = 1 (hier a = 2 und b = 1)
2
1 - h h - 1
Bemerkung zu ————— = ————— : Dies ist ein Spezialfall der Regel:
-h h
a - b b - a 18 - 12 6 -6 12 - 18
————— = —————. Beispiel ——————— = —— = —— = ——————— Merke!
c - d d - c 2 - 7 -5 5 2 - 7
a - b
Nebenbei erwähnt: Ähnlich: ————— = - 1 Merke!
b - a
3 2
Aufgabe: Zeige, das Schaubild einer ganzrationalen Funktion f mit f(x) = ax + bx + cx + d
3
b 2b bc
ist punktsymmetrisch zu seinem Wendepunkt W( - —— | ———— - —— + d).
3a 2 3a
27a
1 b
Lösung: Bevor wir -(f(w + h) + f(x - h)) mit x = - —— berechnen, vereinfachen wir die
2 w w w 3a
einzelnen Potenzen nach den Formeln (a + b) + (a - b) = 2a
2 2 2 2
(a + b) + (a - b) = 2(a + b )
3 3 3 2
und (a + b) + (a - b) = 2(a + 3ab )
b
Somit erhalten wir mit x = - ——:
w 3a
3
a 3 a 3 3 2 b 2
-(x + h) + -(x - h) = ax + 3ax h = - ———— - bh
2 w 2 w w w 2
27a
3
b 2 b 2 2 b 2
-(x + h) + -(x - h) = bw + bh = ——— + bh
2 w 2 w x 2
9a
c c bc
-(x + h) + -(x - h) = cx = - ——
2 w 2 w w 3a
3
1 2b bc
Somit: -(f(x + h) + f(x - h)) = ———— - —— + d = y-Wert des Wendepunktes
2 w w 2 3a
27a
Was bedeutet stetige Ergänzung?
Das bedeutet:
Du hast eine stetige Funktion f, die auf dem Intervall (a,b)\{x } definiert ist.
0
Existiert nun (von recht und von links) lim f(x) = y , so ist folgende Funktion g stetig:
x->x 0
0
g(x) = f(x) für xε(a,b)\{x } und g(x ) = y .
0 0 0
Man sagt dann: f wurde bei x stetig ergänzt.
0
Die beiden stetigen Funktion f und g sind gleich ... bis auf den kleinen Unterschied, dass
g einen größeren Definitionsbereich hat und bei x auch noch stetig ist, während f bei
0
x eine Lücke hat. Im folgenden nenne ich die neue Funktion g auch f.
0
sin(x)
Klassisches Beispiel: f(x) = —————— D = R\{0}
x f
sin(x)
Diese Funktion hat bei x = 0 eine Lücke mit lim f(x) = lim —————— = 1 (bekannter Grenzwert!)
0 x->0 x->0 x
Erweitere ich den Definitionsbereich mit f(0) = 1, dann ist f eine auf R stetige
Funktion, denn lim f(x) = f(0) = 1.
x->0
1
Ein beliebtes Gegenbeispiel ist f(x) = sin - (x≠0).
x
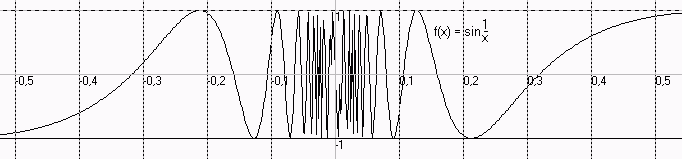
Diese Funktion ist zwar beschränkt (|f(x)|≤1) aber lim f(x) existiert nicht.
x->0
f kann also nicht mit passendem f(0) stetig fortgesetzt werden.
Wie ich auch f(0) definieren würde, f(0)=0 oder f(0)=1 oder sonst wie, f wird bei
Fortsetzung unstetig bei x = 0.
0
1
Anders ist es bei der Funktion f(x) = x·sin- (x≠0).
x
Da lim |f(x)| ≤ lim |x| = 0, ist ist lim f(x) = 0
x->0 x->0 x->0
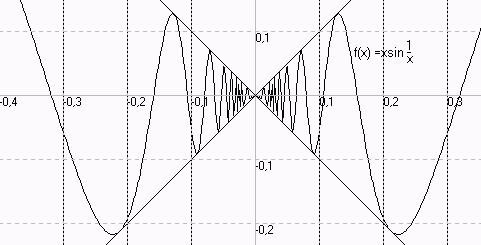
und mit f(0) = 0 haben wir eine stetige Ergänzung von f.
Weitere Beispiele: Siehe Schaubilder x 1 f(x) = ———— nicht definiert bei x = 0, stetige Ergänzung f(x) = ————— , xεR 3 0 2 x +x x + x 2 2x 2x f(x) = ————— nicht definiert bei x = 0, stetige Ergänzung f(x) = —————, xεR. 3 0 2 x + x x + 1 Hier genügte einfach, den Bruchterm zu kürzen (Zähler und Nenner geteilt durch x). 1 Gegenbeispiel: f(x) = -, xεR kann bei x = 0 nicht stetig ergänzt werden, da x 0 1 lim - nicht existiert. Siehe Schaubild. x->0 x
Ich soll einen Vektor durch andere darstellen. Wie mache ich das?
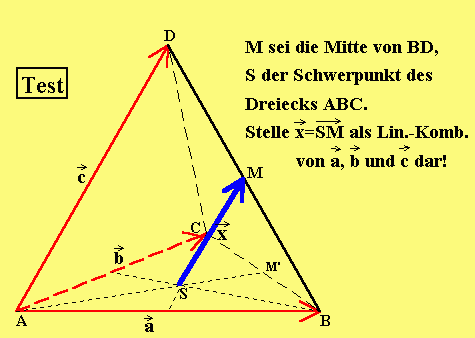
Lösung:
-> ——> ——> ——> ——>
x = SM = SA + AB + BM nach Definition der
Addition von Vektoren.
Zwischenrechnung:
——> 1——> 1 -> ->
BM = -BD = -(-a + c ).
2 2
——> 2——>
SA = - -AM' für M'=Mitte von AC.
3
Der Schwerpunkt teilt ja die Schwerelinie im
Verhältnis AS:SM' = 2:1. (AM' hat also 3 Teile.)
——> -> 1——> -> 1 -> -> 1 -> ->
AM' = a + -BC = a + -(-a + b ) = -(a + b ).
2 2 2
Somit ergibt sich:
-> 2 1 -> -> -> 1 -> ->
x = - -·-(a + b ) + a + -(-a + c )
3 2 2
1-> 1-> 1->
= -a - -b + -c .
6 3 2
—————————————
Wer kann mir erklären: Was versteht man unter
linearer (Un-)Abhängigkeit von Vektoren?
Antwort: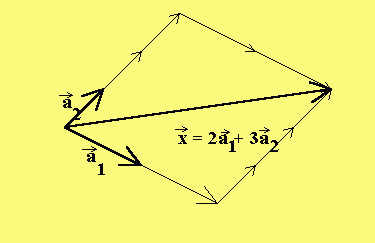
Zuerst einmal: Was heißt LKB (Linearkombination)?
-> -> -> -> ->
Definition: x ist LKB von a , a , a , ..., a , wenn es
1 2 3 n
reelle Zahlen k , k , k , ..., k so gibt, dass
1 2 3 n
-> -> -> -> ->
x = k a + k a + k a + ... k a ist.
1 1 2 2 3 3 n n
-> -> -> ->
Man sagt in diesem Fall auch: x ist linear abhängig von a , a ..., a .
1 2 n
-> -> -> -> -> ->
Hier im Beispiel ist x LKB von a und a , da x = 2a + 3a ist.
1 2 1 2
0 1 0
Gegenbeispiel: ( 0 ) kann nicht als LKB von ( 0 ) und ( 1 )
1 0 0
0 1 0
dargestellt werden: Für keine k und k ist ( 0 ) = k ( 0 ) + k ( 1 )!
1 2 1 1 0 2 0
-> -> -> ->
Definition: Die Vektoren a , a , a , ... ,a sind linear abhängig, wenn sich
1 2 3 n
einer dieser Vektoren als Linearkombination der übrigen darstellen lässt.
-> -> -> -> ->
z.B. a = k a + k a + k a + ... + k a für passende Zahlen k , k , ... ,k ε R.
1 2 2 3 3 4 4 n n 2 3 n
Im Normalfall kann man dann jeden Vektor als Linearkombination der übrigen darstellen:
-> 1 -> -> -> ->
z.B. a = ——(a - k a - k a - ... - k a ). Aber nur im Normalfall. Hier: k ≠ 0.
3 k 1 2 2 3 3 n n 3
3
Um nachzuweisen, ob eine Menge von Vektoren linear abhängig ist, müßte ich also prüfen,
ob der erste Vektor LKB der restlichen ist. Falls nicht: Ist der zweite Vektor LKB der
restlichen u.s.w. Das ist zu umständlich! siehe hier Lösung zur 2. Aufgabe.
Deshalb definiert man gern das Gegenteil, dessen Negation natürlich äquivalent zur gegebenen Definition ist.
-> -> ->
Definition: a , a , ... ,a sind linear unabhängig, wenn folgende Implikation gilt:
1 2 n
-> -> -> ->
k a + k a + ... + k a = 0 => k = 0, k = 0, ... ,k = 0 (Betonung auf "=>").
1 1 2 2 n n 1 2 n
Man sagt auch:
-> -> ->
Die Vektorgleichung k a + k a + ... + k a = 0 hat nur die triviale Lösung k = 0, k = 0, ... ,k = 0.
1 1 2 2 n n 1 2 n
Dann kann man nämlich keinen dieser Vektoren als Linearkombination der übrigen darstellen.
-> 1 -> 2 -> ->
Beispiel: a) a = ( 2 ) und a = ( 4 ) sind linear abhängig (parallel), da a = 2a .
1 3 2 6 2 1
-> 1 -> 1 -> 7
b) a = ( 2 ), a = ( 0 ) und a = ( 2 ) sind linear abhängig.
1 3 2 0 3 3
-> -> -> -> -> ->
Beweis: a ist Linearkombination von a und a , nämlich a = a + 6a .
3 1 2 3 1 2
Man kann es auch folgendermaßen beweisen:
-> -> ->
k a + k a + k a = 0 hat eine nicht triviale Lösung, nämlich k = -1, k = -6, k = 1.
1 1 2 2 3 3 1 2 3
(Das ist nicht die einzige Lösung: eine weitere wäre zum Beispiel k = 1, k = 6, k = -1
1 2 3
-> -> ->
Hinweis: Die Vektorgleichung k a + k a + k a = 0 führt auf das LSG:
1 1 2 2 3 3
| k + k + 7k = 0 | | k + k + 7k = 0 | | k beliebig |
| 1 2 3 | | 1 2 3 | | 3 |
| | | | | |
| 2k + 2k = 0 | äquivalent zu | 2k + 2k = 0 | mit der Lösung | k = - k |
| 1 3 | | 1 3 | | 1 3 |
| | | | | |
| 3k + 3k = 0 | | 0 = 0 | | k = - 6k |
Aber das ist eine andere Geschichte (Lösung des homogenen linearen Gleichungssystems).
Was ist ein
Koeffizientenvergleich?
Die Theorie stammt aus der Vektorrechnung,
die Praxis findet sich überall.
Einführendes Beispiel
Fangen wir vor der Theorie mit einem klassischen Beispiel an:Beispiel 1
Es soll eine Stammfunktion von
16 1
f(x)= —————— = ——————————
2 (x-2)(x+2)
x - 4
bestimmt werden. Dies macht man mit Hilfe der Partialbruchzerlegung:
16 A B A(x + 2) + B(x - 2)
Ansatz: —————— = ————— + —————. Bringt man die rechte Seite auf den Hauptnenner ———————————————————
2 x - 2 x + 2 2
x - 4 x - 4
und vergleicht man die Zähler
so erhält man: 16 = A(x + 2) + B(x - 2), also 0·x + 16 = (A + B)x + 2A - 2B.
Jetzt macht man den Koeffizientenvergleich:
Man vergleicht die Vorzahlen (Koeffizienten) vor x und den Rest und erhält das lineare Gleichungssystem
0 = A + B
( )
16 = 2A - 2B
mit der Lösung A = 4 und B = -4.
16 4 4 |x - 2|
Somit ist f(x) = ————— = ————— - ————— und eine Stammfunktion F(x) = 4 ln|x - 2| - 4 ln|x + 2| = 4ln|—————| .
2 x - 2 x + 2 |x + 2|
x - 4
Warum kann man hier aus einer Gleichung 16 = (A + B)x
+ 2A - 2B zwei Gleichungen
0 = A + B
( )
16 = 2A - 2B
erhalten? Das soll jetzt tiefer untersucht werden.Direkte Antwort dazu:
16 = (A + B)x + 2A - 2B soll ja für alle x (aus dem Definitionsbereich) gelten. Dann kann ich schließen:
Da die Gleichung für x = 0 erfüllt sein soll, folgt 16 = (A + B)·0 + 2A - 2B. Also 16 = 2A - 2B. Da die Gleichung für x = 1 erfüllt sein soll, folgt 16 = (A + B)·1 + 16.Vorausgreifend zur nun folgenden theoretischen Begründung lautet die vertiefte Antwort dazu:
Die Funktionen
f : x ——> 1
0
f : x ——> x
1
2
f : x ——> x (wird hier nicht benötigt)
2
...
sind linear unabhängig. Deshalb folgt aus
a f (x) + a f (x) + a f (x) + ... = b f (x) + b f (x) + b f(x) + ...
0 0 1 1 2 2 0 0 1 1 2 2
a = b , a = b , a = b , ...
0 0 1 1 2 2
Hier kann man also bei 0·x + 16 = (A + B)x + 2A - 2B die "Koeffizienten"
a = 0 und b = A + B sowie a = 16 und b = 2A - 2B "vergleichen".
0 0 1 1
0 = A + B
Man erhält so das lineare Gleichungssystem ( ) mit der Lösung A = 4 und B = -4.
16 = 2A - 2B
Theorie
-> -> ->
Definition: a , a , ... ,a sind linear unabhängig, wenn folgende Implikation gilt:
1 2 n
-> -> -> ->
k a + k a + ... + k a = 0 => k = 0, k = 0, ... ,k = 0 (Betonung auf "=>").
1 1 2 2 n n 1 2 n
-> -> ->
(a , a , ... ,a Vektoren, k , k , ...,k ε R)
1 2 n 1 2 n
|
-> ->
Insbesondere sind zwei von Null verschieden Vektoren a und b linear unabhängig, wenn
-> -> -> ->
b kein Vielfaches von a ist, wenn also für kein kεR gilt: b = ka .
-> -> ->
(Denn sonst hätte die Gleichung k a + k b = 0 die nicht triviale Lösung k = k und k = -1.)
1 2 1 2
|
-> -> ->
Drei von Null verschieden Vektoren a , b und c sind linear unabhängig, wenn kein Vektor
dieser drei Vektoren Linearkombination der übrigen beiden ist.
|
-> -> ->
Satz: Sind die Vektoren a , a , ... ,a linear unabhängig und gilt
1 2 n
-> -> -> -> -> ->
a a + a a + ... + a a = b a + b a + ... + b a (*), so folgt daraus:
1 1 2 2 n n 1 1 2 2 n n
a = b , a = b , ... a = b ("Die Koeffizienten sind gleich!")
1 1 2 2 n n
Beweis: Durch Umformung von (*) erhält man
-> -> ->
(a - b )·a + (a - b )·a + ... + (a - b )·a = 0 und wegen der linearen Unabhängigkeit
1 1 2 2 n n n
die Behauptung.
|
Satz:Im Vektorraum der ganzrationalen Funktionen
sind für nεN die folgenden Funktionen
linear unabhängig:
f : x ——> 1
0
f : x ——> x
1
2
f : x ——> x
2
...
n
f : x ——> x
n
Beweis: Sei af (x) + a f (x) + a f (x) + a f (x) = 0 für alle xεR.
0 1 1 2 2 3 3
2 3 4 n
Sei also a + a x + a x + a x + a x + ... + a x = 0 (0)
0 1 2 3 4 n
Durch wiederholtes Ableiten erhält man die Beziehungen:
2 3 n-1
a + 2a x + 3a x + 4a x + ... + na x = 0 (1)
1 2 3 4 n
2 n-2
2a + 2·3a x + 3·4a x + ... (n-1)·na x = 0 (2)
2 3 4 n
....
n!a = 0 (n)
n
Die Gleichungen (0), (1), (2), ... (n) müssen für alle x erfüllt sein:
x=0 in (0) eingesetzt ergibt a = 0,
0
x=0 in (1) eingesetzt ergibt a = 0,
1
x=0 in (2) eingesetzt ergibt a = 0,
2
...
x=0 in (n) eingesetzt ergibt a = 0.
n
Somit ist die lineare Unabhängigkeit der Funktionen nachgewiesen.
Der Beweis mit vollständiger Induktion (ohne "...") ist
hier ganz geradlinig und sei dem Leser überlassen.
|
Ähnlich trickreich beweist man für weitere Funktionenklassen die lineare Unabhängigkeit:
Satz:Im Vektorraum der Funktionen sind für
nεN die folgenden Funktionen linear
unabhängig:
f : x ——> 1
0
x
f : x ——> e
1
2x
f : x ——> e
2
...
nx
f : x ——> e
3
|
Satz:Im Vektorraum der Funktionen sind für
nεN die folgenden Funktionen linear
unabhängig:
f : x ——> sinx,
0
f : x ——> sin2x
1
f : x ——> sin3x
2
...
f : x ——> sin(nx)
3
|
|
Wir können auch Funktionen verschiedenster Art
kombinieren. Dass zum Beispiel die Funktionen u(x)= x,
Und überhaupt: Kann eine periodische Funktion Linearkombination nichtperiodischer Funktionen sein? Und wenn Du mit diesen pauschalen Argumenten Deine skeptischen Mitmenschen immer noch nicht überzeugt hast, denn zeige, dass die Gleichung
π
Setzte in (*) x = 0, x = - und x = π . Dann erhältst Du das lineare Gleichungssystem:
2
c = 0
π π/2
a·- + b + c·2 = 0
2
π
a·π + c·2 = 0.
Dieses Gleichungssystem hat nur die triviale Lösung a = 0, b = 0 und c = 0.
|
Weitere Beispiele
Beispiel 2:
2
x - 2x + 1
Gesucht ist die Asymptote y = ax + b der Funktion f(x) = ——————————
2x-1
Lösung: a und b müssen also so bestimmt werden, dass
lim(f(x) - (ax + b) = 0
x->∞
Stellen wir die Differenz als einen Bruch dar, so erhalten wir:
2 2
x - 2x - 1 - (ax+b)(2x-1) (1 - 2a)x + (-2+a-2b)x - 1 + b
f(x) - (ax + b) = ————————————————————————— = ——————————————————————————————
2x - 1 2x - 1
2
Der Grenzwert wird Null, wenn die Koeffizienten von x und x Null werden,
d.h. wenn 1 - 2a = 0 und a - 2b - 2 = 0 wird.
1 3
Die Lösung des Gleichungssystems ist a = - und b = - -.
2 4
1 3
Die Gleichung des Asymptote ist also y = -x - -.
2 4
1 3 -7/4
Probe: lim (f(x) - (-x - -) = lim ———— = 0.
x->oo 2 4 x->oo 2x-1
Berechnung (Aufg. 1c) ist auch über
über Polynomdivision möglich.
Beispiel 3:
Beweis eines Satzes aus der Vektorrechnung mit Hilfe des Koeefizientenvergleichs:
Im Parallelogramm halbieren sich die Diagonalen
.
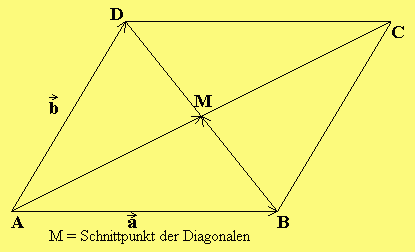
Voraussetzung:
-> ——> -> ——>
a = AB und b = AC sind linear unabhängig.
(Sonst würde das Viereck die Fläche 0 haben.)
Behauptung: M halbiert die Diagonalen.
——> ——> ——> ——>
Beweis: Sei AM = x AC und BM = y BD
——> ——> ——>
Dann gilt: AM = AB + BM
——> -> ——>
xAC = a + yBD
-> -> -> -> ->
x(a + b ) = a + y(-a + b )
-> -> -> ->
x a + x b = (1 - y)a + yb.
Koeffizentenvergleich ergibt:
x = 1 - y 1 1
( ). Daraus folgt: x = - und y = - .
x = y 2 2
Beispiel 4:
Als nächstes Beispiel beweisen wir mit Hilfe des Koeffizientenvergleichs den Schwerpunktsatz:
"Die Schwerelinien teilen sich im Verhältnis 2:1.
In der folgenden Zeichnung sei M die Mitte von BC und M die Mitte von AC.
a b
S sei der Schnittpunkt der Schwerelinien (Seitenhalbierenden) AM und BM .
a b
—— —— ——> ——> 2
Wenn AS:SM = 2:1 ist (AM also drei Teile), muss gezeigt werden dass AS = x·AM für x = -.
a a a 3
-> ——> -> ——>
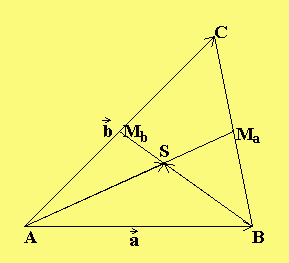
Beweis: Die Vektoren a = AB und b =AC sind linear unabhängig.
——> ——> ——> ——> 2 2
Sei AS = xAM und BS = yBM . Zu zeigen ist: x = - und y = -.
a b 3 3
——> -> ->
Für den Beweis benötigen wir folgendes: BC = b - a.
——> 1——> 1-> 1-> ——> ——> ——> -> 1-> 1-> 1-> 1->
BM = -BC = -b - -a . AM = AB + BM = a + -b - -a = -a + -b .
a 2 2 2 a a 2 2 2 2
——> -> ——>
Jetzt können wir loslegen: AS = a + BS
——> -> ——>
xAM = a + yBM
a b
1-> 1-> -> -> 1->
x(-a + -b ) = a + y(-a + -b )
2 2 2
x-> x-> -> y->
-a + -b = (1-y)a + -b
2 2 2
x x y
Der Koeffizientenvergleich liefert - = 1-y und - = -.
2 2 2
2
Die Lösung dieses lin. Gleichungssystems ist x = y = - ∎
3
Beispiel 5:
Im diesem Beispiel soll bewiesen werden, dass die Funktion F mit
t
36·e
F(t) = —————— für passendes kεR und GεR
t
1 + e
die Differentialgleichung (des logistischen Wachstums)
F'(t) = k·F(t)·[G - F(t)]
erfüllt.
Dazu differenzieren wir F(t) und setzten dies in die Differentialgleichung ein und formen um:
F'(t) = k·F(t) ·[G - F(t)]
t t t
36·e 36e 36e
————————— = k·————————·[G - ——————]
t 2 t t
(1 + e ) 1 + e 1 + e
t t t t
36·e 36ke G+Ge - 36e
————————— = ———————·[——————————]
t 2 t t
(1 + e ) 1 + e 1 + e
t t t
36·e 36·k·(G + (G-36)·e )·e
————————— = ———————————————————————
t 2 t 2
(1 + e ) (1 + e )
Diese Gleichung wird genau dann erfüllt, wenn
t
1 = k·G + k(G-36)·e (*)
für alle tεR erfüllt ist.
Da die Funktionen t ——> 1 und
t
t ——> e offensichtlich linear unabhängig sind, können wir den
Koeffizientenvergleich in Gleichung (*) durchführen.
1 = k·G 1
( ) mit der eindeutig bestimmten Lösung G = 36 und k = ——
0 = k·(G-36) 36
|
Zur Kettenregel
Was muss ich bei der Kettenregel
beachten?
Antwort: Zunächst musst Du verstehen, wie zwei
Funktionen verkettet werden.Das hört sich schlimmer an als es ist.
Im wesentliche ersetzt Du x in u(x) durch einen weiteren Term v(x) und erhältst so eine neue Funktion f mit
Beispiel:
2
u(x) = x v(x) = 3x + 4
2 2
=> f(x) = u(v(x)) = (v(x)) = (3x + 4)
Du kannst auch folgendermaßen rechnen:
2
f(x) = u(v(x)) = u(3x + 4) = (3x + 4) .
Wem das klar ist, der kann gleich zu den Übungen gehen.
Hier noch einige Bemerkungen zur Vertiefung des Verständnisses:
Ich erläutere die Verkettung zunächst ausführlich, zunächst ohne Verwendung von
Variablen. (Ob die Variable x oder t oder sonst wie heißt, ist logisch unerheblich.)
Die Funktionen v und u seien folgendermaßen definiert:
v: "Addiere zum 3-fachen 4!" und u: "quadriere!"
Damit sind folgende Zuordnungen definiert:
v u
1 ——> 7 1 ——> 1
2 ——> 10 2 ——> 4
3 ——> 13 3 ——> 9
4 ——> 16 4 ——> 13
2
x ——> 3x + 4 x ——> x
Die Vorschrift für die Verkettung der Funktionen lautet nun:
"Addiere zum 3-fachen 4 und quadriere das Ergebnis!"
Zuerst wird die Zuordnungsvorschrift für v befolgt, dann die für u.
v u
1 ——> 7 ——> 49
2 ——> 10 ——> 100
3 ——> 13 ——> 169
4 ——> 16 ——> 256
2
x ——> 3x + 4 ——> (3x + 4)
Das ergibt also die Zuordnung für f = uov (Warum nicht "vou"? siehe unten).
f
1 ————————————————> 49
2 ————————————————> 100
3 ————————————————> 169
4 ————————————————> 256
2
x ————————————————> (3x + 4)
Man sagt: u wurde mit v verkettet und schreibt dafür
f = uov ("u Kringel v", gesprochen "u nach v")
f wird also definiert durch f(x) = u(v(x))
xεD mit D = {xεR | xεD und v(x)εD }.
f f v u
Der Definitionsbereich von f wird durch die Bedingung
für x ε D und v(x) ε D diktiert.
v u
Dies kann zu drastischen Einschränkungen führen, wie am folgenden
Beispiel gezeigt werden soll:
- -
u: x-> \/x , x ε R v: x -> - \/x , x ≥ 0
———————
-
f: x -> \/ - \/x . Hier ist nur x=0 möglich: D = {0}
f
Es ist also f(x) = (uov)(x) = u(v(x))
Daher auch die paradoxe Reihenfolge von u und v in f = uov ("u nach v").
Bei
den folgenden Übungen wird die Kettenregel eingeübt:
Kettenregel.
f(x) = u(v(x)) => f'(x) = u'(v(x))·v'(x)
"äußere Ableitung mal innere Ableitung".
1. Gegeben u(x) und v(x). Schreibe auf: u'(x) und v'(x), sowie f(x) = u(v(x)) und f'(x) = u'(v(x))·v'(x).
3 2
Beispiel: u(x) = x v(x) = 4 - 3x => u'(x) = 3x v'(x) = - 3
3 2
f(x) = u(v(x)) = (4 - 3x) f'(x) = u'(v(x))·v'(x) = 3(4 - 3x) ·(-3)
3 2
Somit: f(x) = (4 - 3x) hat die Ableitung f'(x) = -9(4 - 3x)
3
a) u(x) = 2x v(x) = 7x - 11
- 2
b) u(x) =\/x v(x) = 25 - x
1
c) u(x) = - v(x) = 5 - 3x
x
2
d) u(x) = x v(x) = sinx
Erst ab Klasse 13 (Kenntnis von exp und ln wird benötigt!)
x 1 2
e) u(x) = e v(x) = - -x
2
2
f) u(x) = lnx v(x) = x + 1 (nicht mehr für B-W)
Lösungen
Nun wird es Dir nicht schwer fallen, auch die folgenden
Funktionen abzuleiten:2. Übung zur Kettenregel: Leite ab!
Verwende die Regel: "Äußere Ableitung · innere Ableitung"!
11 1 3
a) f(x) = 3(5x - 7) b) f(x) = -(3 - 4x)
2
c) f(x) = 3sin2x d) f(x) = 2cos3x
3 2
e) f(x) = —————— f) f(x) = —————————
2x - 1 3
(2x - 4)
————— - 2
g) f(x) = 4\/1- 3x h) f(x) = (1 - \/x)
Erst ab Klasse 13 (Kenntnis von exp und ln wird benötigt!)
2 3 - 2x 2 -
i) f(x) = -e k) f(x) = 4ln(3x - \/x) (nicht mehr in B-W)
3
LösungenAls nächste Übung musst Du die Funktion u und v bei f = uov angeben und damit die angewendete Kettenregel überzeugend darstellen. Erst, wenn Dir dies gelingt
3. Übung zur Kettenregel: Finde passende Funktion u und v mit f = uov, mache die Probe f(x) = u(v(x)) und leite nach der Kettenregel ab!
Beachte u ist die äußere Funktion (das was später berechnet wird), v ist die innere Funktion (das was zuerst berechnet wird).
—————
1 9 /2
a) f(x) = ——(5 - 4x) b) f(x) = \/x - 25
18
1 3 1 3
c) f(x) = -sin x d) f(x) = -sinx
3 3
—————————
/ 2 2
e) f(x) = \/1 - sin x f) f(x) = (4sinπx + 3cosπx)
Erst ab Klasse 13 (Kenntnis von exp und ln wird benötigt!)
3
1 (x-2) 4
g) f(x) = -e h) f(x) = ln(2-3x) (nicht mehr in B-W)
2
Lösungen
Jetzt kommen einige Übungen für
Fortgeschrittene:4. Übung zur Kettenregel:
1
a) f(x) = ————————————————— (Mit Ketten- oder Quotientenregel möglich)
3 2
4x + 5x - 7x + 8
—————
/5
b) f(x) = / - - 1
\/ x
2x + 1 4
c) f(x) = (——————) (Ketten- und Quotientenregel erforderlich)
3x - 1
————— 3 4
d) f(x) = (\/x - 3 + ————) (Nach dem Ableiten auf den Hauptnenner bringen!)
———
\/x-3
e) f(x) = sin(sin(sinx))
Erst ab Klasse 13 (Kenntnis ln wird benötigt!)
2x - 1
f) f(x) = ln ——————
x + 1
———
g) f(x) = \/lnx
Lösungen
5. Übung
Was ist die Ableitung von
1 1
- -
x x x x
f(x)=2 , g(x) = x , h(x)= 2 und i(x) = x ?
Lösungen
Lösungen zur 1. Übung zur Kettenregel
3
a) u(x) = 2x v(x) = 7x - 11
2
u'(x) = 6x v'(x) = 7
3
f(x) = u(v(x)) = 2(7x - 11)
2 2
f'(x) = u'(v(x))·v'(x) = 6(7x - 11) ·7 = 42(7x - 11)
- 2
b) u(x) = \/x v(x) = 25 - x
1
u'(x) = ————— v'(x) = - 2x
-
2\/x
——————
/ 2 2 2
f(x) = u(v(x)) = \/25 - x (Schaubild: Halbkreis da y + x = 25)
1 x
f'(x) = u'(v(x))·v'(x) = —————————— ·(- 2x) = - ——————————
—————— ——————
/ 2 / 2
2\/25 - x \/25 - x
1
c) u(x) = - v(x) = 5 - 3x
x
1
u'(x) = - —— v'(x) = - 3
2
x
1
f(x) = u(v(x)) = ——————
5 - 3x
1 3
f'(x) = u'(v(x))·v'(x) = - —————————·(-3) = —————————
2 2
(5 - 3x) (5 - 3x)
2
d) u(x) = x v(x) = sinx
u'(x) = 2x v'(x) = cosx
2 2
f(x) = u(v(x)) = (sinx) (Mit Klammerersparnisregel geschrieben: f(x) = sin x)
f'(x) = u'(v(x))·v'(x) = 2sinx·cosx (beliebter Fehler: f'(x) !falsch=! 2cosx!)
x 1 2
e) u(x) = e v(x) = - -x
2
x
u'(x) = e v'(x) = - x
1 2
- -x
2 1
f(x) = u(v(x)) = e Nebenbei bemerkt: Gauß'sche Glockenkurve: ————f(x)
——
\/2π
1 2 1 2
- -x - -x
2 2
f'(x) = u'(v(x))·v'(x) = e ·(-x) = -xe
2
f) u(x) = lnx v(x) = x + 1
1
u'(x) = - v'(x) = 2x
x
2
f(x) = u(v(x)) = ln(x + 1)
1 2x
f'(x) = u'(v(x))·v'(x) = —————·2x = ——————
2 2
x + 1 x + 1
Lösungen zur 2. Übung zur Kettenregel
11 1 3
a) f(x) = 3(5x - 7) b) f(x) = -(3 - 4x)
2
10 2
f'(x) = 165(5x - 7) f'(x) = -6(3 - 4x)
c) f(x) = 3sin2x d) f(x) = 2cos3x
f'(x) = 6cos2x f'(x) = - 6sin3x
3 2
e) f(x) = —————— f) f(x) = —————————
2x - 1 3
(2x - 4)
6 12
f'(x) = - ————————— f'(x) = - —————————
2 4
(2x - 1) (2x - 4)
————— - 2
g) f(x) = 4\/1- 3x h) f(x) = (1 - \/x)
- -
6 1 - \/x \/x - 1
f'(x) = - ————————— f'(x) = - —————— = ———————
—————— - -
\/1 - 3x \/x \/x
2 3 - 2x 2 -
i) f(x) = -e k) f(x) = 4ln(3x - \/x)
3
4 3 - 2x 4 1
f(x) = - -e f'(x) = ———————— ·(6x - ————)
3 2 - -
3x - \/x 2\/x
Lösungen zur 3. Übung zur Kettenregel
—————
1 9 /2
a) f(x) = ——(5 - 4x) b) f(x) = \/x - 25
18
1 9 - 2
u(x) = ——x v(x) = 5 -4x u(x) = \/x v(x) = x - 25
18
—————
1 9 ————— /2
f(x) = u(v(x)) = ——(v(x)) f(x) = u(v(x)) = \/(v(x) = \/x - 25
18
1 9
= ——(5 - 4x)
18
1 8 1
u'(x) = -x v'(x) = - 4 u'(x) = ————— v'(x) = 2x
2 -
2\/x
f'(x) = u'(v(x))·v'(x) f'(x) = u'(v(x))·v'(x)
8 x
= - 2(5 -4x) = —————————
—————
/2
\/x - 25
1 3 1 3 1 3 1 3
c) f(x) = -sin x = -(sinx) d) f(x) = -sinx = -sin(x ) (Achtung!)
3 3 3 3
1 3 1 3
u(x) = -x v(x) = sinx u(x) = -sinx v(x) = x
3 3
1 3 1 1 3
f(x) = u(v(x)) = -(v(x)) f(x) = u(v(x)) = -sin(v(x)) = -sinx
3 3 3
1 3
= -(sinx)
3
2 1 2
u'(x) = x v'(x) = cosx u'(x) = -cosx v(x) = 3x
3
f'(x) = u'(v(x))·v'(x) f'(x) = u'(v(x))·v'(x)
2 1 3 2 2 3
= (sinx) ·cosx = -cosx ·3x = x cosx
3
Hier verliert man leicht den Überblick! Beachte: bei c) wird zuerst der Sinus berechnet
und dann potenziert. Bei d) wird zuerst potenziert und dann der Sinus berechnet.
—————————
/ 2 2
e) f(x) = \/1 - sin x f) f(x) = (4sinπx + 3cosπx)
- 2 2
u(x) = \/x v(x) = 1 - (sinx) u(x) = x v(x) =4sinπx + 3cosπx
—————— 2
f(x) = u(v(x)) = \/(v(x)) f(x) = u(v(x)) = (v(x))
—————————
/ 2 2
= \/1 - sin x = (4sinπx + 3cosπx)
1
u'(x) = ———— v'(x) = - 2sinxcosx u'(x) = 2x v'(x) = 4πcosπx - 3πsinπx
-
2\/x
f'(x) = u'(v(x))·v'(x) f'(x) = u'(v(x))·v'(x)
sinxcosx
= - ——————————— = 2(4sinπx + 3cosπx)·(4πcosπx - 3πsinπx)
————————
/ 2
\/1 - sin x
3
1 (x-2) 4 2
g) f(x) = -e h) f(x) = ln(2-3x) = 4ln(2-3x) für x < -
2 3
1 x 3 4
u(x) = -e v(x) = (x-2) u(x) = lnx v(x) = (2 - 3x)
2
1 v(x) 4
f(x) = u(v(x)) = -e f(x) = u(v(x)) = ln(v(x)) = ln (2 - 3x)
2
3
1 (x-2)
= -e
2
1 x 2 1 3
u'(x) = -e v'(x) = 3(x-2) u'(x) = - v'(x) = -12(2 - 3x)
2 x
f'(x) = u'(v(x))·v'(x) f'(x) = u'(v(x))·v'(x)
3 3
3 2 (x-2) 12(2-3x) 12
= -(x-2) e = - ————————— = - ———————
2 4 2 - 3x
(2 - 3x)
Das Ergebnis von h) hätte man (für einen kleineren Definitionsbereich) schneller
2 2
mit der Umformung f(x) = 4ln(2 - 3x) erreicht. (Hier x < - oder x ≠ -.)
3 3
Lösungen zur 4. Übung zur Kettenregel
1 3 2 -1
a) f(x) = ————————————————— = (4x + 5x - 7x +8) (auch Quotientenregel möglich)
3 2
4x + 5x - 7x + 8
2
3 2 -2 2 -12x - 10x + 7
f'(x) = -(4x + 5x - 7x +8) (12x + 10x -7) = ——————————————————————
3 2 2
(4x + 5x - 7x + 8)
5
- ——
————— 2
/5 x 5
b) f(x) = / - - 1 f'(x) = —————————— = - ————————————
\/ x ————— —————
/5 /5
/ - - 1 2 / - - 1
2\/ x 2x \/ x
3
2x + 1 4 2x + 1 3 2(3x -1) - 3(2x + 1) 20(2x + 1)
c) f(x) = (——————) f'(x) = 4(——————) · ———————————————————— = - ——————————
3x - 1 3x - 1 2 5
(3x - 1) (3x - 1)
————— 3 4 ————— 3 3 x - 6
d) f(x) = (\/x - 3 + —————) f'(x) = 4(\/x - 3 + ——————) · —————————
———— ——— 3
\/x-3 \/x-3 -
2
2(x - 3)
3
4x (x - 6)
= ——————————
3
2(x - 3)
e) f(x) = sin(sin(sinx)) = u(v(x)) für u(x) = sin(x) und v(x) = sin(sin(x))
wobei v(x) = p(q(x)) für p(x) = sin(x) und q(x) = sin(x).
=> u'(x) = cosx und v'(x) = p'(q(x))q'(x) = cos(q(x))cosx = cos(sinx)cosx
f'(x) = u'(v(x))·v'(x) = cos(v(x))·v'(x) = cos(sin(sinx))·cos(sinx)·cosx
Bemerkung: Solche eine Funktion ist rein akademischer Struktur, in Wiklichkeit
kommt sie höchstwahrscheinlich nie vor. Ingenieure müssen sich
allerdings mit noch mehr verschachtelten Funktionen herumschlagen.
2x - 1 1
f) f(x) = ln —————— Nebenbei bemerkt: D = (-oo,-1) U (-, oo) ( U = "vereinigt")
x + 1 f 2
1 3 3 u'
f'(x) = ——————·—————— = ————————————— Regel: y =ln u => y' = ——
2x-1 2 (x + 1)(2x-1) u
———— (x+1)
x+1
——— 1 1 1
g) f(x) = \/lnx => f'(x) = —————·- = ——————— D = [1,oo) D = (1,oo)
——— x ——— f f'
2\/lnx 2x\/lnx
Lösungen zur 5. Übung zur Kettenregel:
x n
Zuerst eine Warnung: Man darf f(x)=2 nicht ableiten wie g(x) = x .
f ist eine Exponentialfunktion (Ableitung siehe unten),
n-1
und g ist eine Potenzfunktion mit g'(x) = n·x .
x-1
Also ja nicht f'(x)=x·2 (falsch!) schreiben!
Zur Ableitung der oben angegeben Potenzfunktionen benötigt man
in erster Linie die folgende Regeln:
1. f(x)=u(v(x)) => f'(x) = u'(v(x))·v'(x) (Kettenregel)
x lna x x·ln(a)
2. a = (e ) = e (nach den Potenzgesetzten)
x x
3. f(x) = e => f'(x)=e (Ableitung der nat. Exp.-Funktion)
4. (uv)' = u'v+uv' (Produktregel)
1
5. f(x)=ln(x) => f'(x)= - (Die Ableitung des nat. Logarithmus)
x
Damit kann ich die vier Funktionen ableiten:
x x·ln(2)
a) f(x) = 2 = e = u(v(x))
x x
mit u(x) = e => u'(x) = e
und v(x) = x·ln(2) => v'(x) = ln(2)
Somit: f'(x) = u'(v(x))·v'(x)
x·ln(2) x x
= e ·ln(2) = 2 ·ln(2) = ln(2)·2
Analoge leitet man g, h und i ab.
x x·ln(x) x·ln(x)
b) g(x) = x = e => g'(x) = e ·(ln(x) + 1)
x
g'(x) = (ln(x)+1)·x
1/x 1/x·ln(2)
c) h(x)= 2 = e
1/x·ln(2) 1 ln(2) 1/x
h'(x)=e ·(-ln(2)·- ) = - —————·2
2 2
x x
1/x 1/x·ln(x)
d) i(x) = x = e
(1/x)·ln(x) 1 1
i'(x)=e ·(- ——·ln(x) + ——)
2 2
x x
1-ln(x) 1/x
i'(x)= ——————— x
2
x
-
Warum ist tan(15°)=2 -\/3?
Jedenfalls behauptet das TTmathe.
Bemerkung: TTmathe rechnet tan(15°) = 0,267 949 192 431
122 706. TTMathe gibt diesen Wert noch als Wurzel aus: Antwort: Die Frage ist berechtigt. Rechnet doch TTMathe nur numerisch und es könnte sein, dass TTmathe nur zufällig einen Näherungswert erwischt hat. (Was bei bei einer Genauigkeit von ca. 18 signifikanten Stellen natürlich äußerst unwahrscheinlich ist.) Tatsächlich stimmt die Behauptung.
Hier der Beweis:
1 - 1 α 1 - cosα
mit cos(30°) = -\/3 und sin(30°) = - sowie tan- = ———————— folgt:
2 2 2 sinα
-
tan15° = 2 - \/3
In einem Diskussionsforum
(de.sci.mathematik) wurden von Hermann Kremer einmal
folgende Werte gepostet:
sin( 0°) = 0 cos( 0°) = 1 sin( 3°) = (sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1)-2*(sqrt(3)-1)*sqrt(sqrt(5)+5))/16 cos( 3°) = (2*(sqrt(3)+1)*sqrt(5+sqrt(5))+sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1))/16 sin( 6°) = (sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1))/8 cos( 6°) = (sqrt(2)*sqrt(5-sqrt(5))+sqrt(3)*(sqrt(5)+1))/8 sin( 9°) = (sqrt(2)*(sqrt(5)+1)-2*sqrt(5-sqrt(5)))/8 cos( 9°) = (sqrt(2)*(sqrt(5)+1)+2*sqrt(5-sqrt(5)))/8 sin(12°) = (sqrt(2)*sqrt(5+sqrt(5))-sqrt(3)*(sqrt(5)-1))/8 cos(12°) = (sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+sqrt(5)-1)/8 sin(15°) = sqrt(2)*(sqrt(3)-1)/4 cos(15°) = sqrt(2)*(sqrt(3)+1)/4 sin(18°) = (sqrt(5)-1)/4 cos(18°) = sqrt(2)*sqrt(sqrt(5)+5)/4 sin(21°) = (2*(sqrt(3)+1)*sqrt(5-sqrt(5))-sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1))/16 cos(21°) = (2*(sqrt(3)-1)*sqrt(5-sqrt(5))+sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1))/16 sin(22,5°) = 1/2*sqrt(2-sqrt(2)) cos(22,5°) = 1/2*sqrt(2+sqrt(2)) sin(24°) = (2*sqrt(3)*(sqrt(5)+1)-sqrt(2)*(sqrt(5)-1)*sqrt(5+sqrt(5)))/16 cos(24°) = (sqrt(2)*sqrt(3)*(sqrt(5)-1)*sqrt(5+sqrt(5))+2*(sqrt(5)+1))/16 sin(27°) = ((sqrt(5)+1)*sqrt(sqrt(5)+5)+(sqrt(5)-1)*(sqrt(5-sqrt(5))-2*sqrt(2)))/16 cos(27°) = ((sqrt(5)+1)*sqrt(sqrt(5)+5)+(sqrt(5)-1)*(sqrt(5-sqrt(5))+2*sqrt(2)))/16 sin(30°) = 1/2 cos(30°) = sqrt(3)/2 sin(33°) = (2*(sqrt(3)-1)*sqrt(sqrt(5)+5)+sqrt(2)*(sqrt(3)+1)*(sqrt(5)-1))/16 cos(33°) = (2*(sqrt(3)+1)*sqrt(sqrt(5)+5)-sqrt(2)*(sqrt(3)-1)*(sqrt(5)-1))/16 cos(36°) = (sqrt(5)+1)/4 sin(36°) = sqrt(2)*sqrt(5-sqrt(5))/4 sin(39°) = (sqrt(2)*(sqrt(3)+1)*(sqrt(5)+1)-2*(sqrt(3)-1)*sqrt(5-sqrt(5)))/16 cos(39°) = (sqrt(2)*(sqrt(3)-1)*(sqrt(5)+1)+2*(sqrt(3)+1)*sqrt(5-sqrt(5)))/16 sin(42°) = (sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1))/8 cos(42°) = (sqrt(2)*sqrt(5+sqrt(5))+sqrt(3)*(sqrt(5)-1))/8 sin(45°) = sqrt(2)/2 cos(45°) = sqrt(2)/2Wozu soll das gut sein?
Ein Beispiel ist die Konstruktion des regelmäßigen n-Ecks, etwa des regelmäßigen 5-Ecks. Bei diesem kann man den Mittelpunktswinkel von 72° mit Hilfe der Formel
-
\/5 -1
cos(72°)=sin(18°)= ——————
4
mit Zirkel und Lineal konstruieren.
sin(10°) läßt sich nicht mit Zirkel und Lineal konstruieren und damit auch nicht ein reglmäßiges, 36-, 18- oder Neuneck mit den Mittelpunktswinkeln 10°, 20° oder 40°.
Anders ausgedrückt: Die Dreiteilung eines 30°- ,60°- oder 120°-Winkels ist mit Zirkel und Lineal unmöglich.
Weitere Werte
Warum berechnet Excel und mein Taschenrechner 9x4-y4+2y2 für x=10864 und y=18817 falsch?
Von Hand ausgerechnet erhalte ich den Wert 1:
9*x^4 - y4 + 2y^2 = 125 372 283 822 342 144 - 125 372 284 530 501 121 + 708 158 978 —————————————————————————— = 1 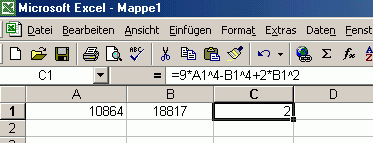 Excel liefert den Wert 2 und mein Taschrechner liefert mir über 1 Million (genau 1 158 978). Was stimmt da nicht? |