Joachim Mohr Mathematik Musik Delphi
5.1 Wellen - fortschreitende Störungen
Mechanische Wellen, z. B. Wasserwellen oder Schallwellen, breiten sich von einem Erreger aus mit einer bestimmten Geschwindigkeit, der Ausbreitungsgeschwindigkeit, aus. Mit Wellen wird Energie, aber kein Stoff transportiert. Wellen können reflektiert und gebrochen werden. Typische Eigenschaften von Wellen sind die Beugung und die Interferenz (Überlagerung).Eine Welle ist die Ausbreitung einer Schwingung im Raum. Eine solche Schwingung breitet sich mit einer bestimmten Geschwindigkeit, der Ausbreitungsgeschwindigkeit c, aus. Die Ausbreitungsgeschwindigkeit c mechanischer Wellen kann berechnet werden mit der Gleichung:
c=λ*f (λ: Wellenlänge), f: Frequenz der Schwinger).
Die Ausbreitungsgeschwindigkeit ist sehr unterschiedlich und hängt in starkem Maße von den jeweiligen Bedingungen ab. In der nachfolgenden Übersicht sind einige Ausbreitungsgeschwindigkeiten zusammengestellt.
Wasserwellen in Meeren ca. 0,5 m/s . . . Erdbebenwellen ca. 5km/s
Schallwellen in Luft bei -20 °C 320 m/s . . . bei 0 °C 332 m/s . . . bei +20 °C 344m/s . . .
5.2 Längs-und Querwellen
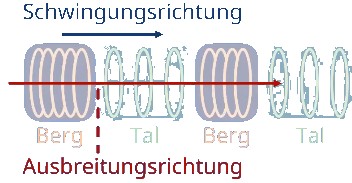
Längswellen=Longitudinalwelle
Die Schwingungen und Welleberge und -täler breiten sich in dieselbe Richtung aus.
Die Schwingungsrichtung uns Ausbreitungsrichtung ist dieselbe.
Beispiel: Schallwellen oder stockender Autoverkehr
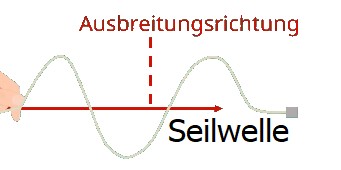
Transwersalwellen
Schwingungen sind senkrecht zur Ausbreitungsrichtung.
Beispiel: Seilwelle, Lichtwelle, La-Ola-Welle.
Transversalwellen sind Polarisierbar.
5.3 Beschreibung von Wellen
Ein Oszillator ist ein hin-und herschwingendes Teilchen.
Die harmonische Welle ist eine Idealisierung der Beschreibung. Amplitude und Frequenz einer Welle sind konstant.
5.4 Wellen in Gleichungen
Für dei Geschwindigkeit einer Welle gilt: c=λ·f, wobei λ die Wellenlänge und f die Freuquenz.
Beispiel Schallwelle: Wellenlänge λ=5,5mm. Frequenz f=40,1kHz ⇒ c=λ·f=0,0085m*401001/s=341m/s.
Eine fortschreitende Sinuswelle hat die Gleichung
´` t x
s(x;t)=s ·sin(2π·(—-—))
T λ
5.5 Überlagerungen von Wellen
Die Interferenz beschreibt die Überlagerung von zwei oder mehr Wellen nach dem Superpositionsprinzip.
Konstruktive Interferenz
Die Wellenberge der einen Welle trifft die Wellenberge der anderen Welle.
Wellenberg fällt auf Welleberg, Wellental fällt auf Wellental.
Es entsteht eine Welle mit gleicher Frequenz mit einer Amplitude, die die Summe der beiden Amplituden ist.
Destruktive Interferenz
Wellenberg fällt auf Wellental, Wellental fällt auf Wellenberg. Bei gleicher Amplitude entsteht eine Auslöschung längs der gesamten Ausbreitungsrichtung.
Anwendung: Kopfhörer, der die Außengeräusche löscht.
Trifft eine Meereswelle mit kleiner Amplitude und großer Wellenlänge auf Land, so entsteht eine Monsterwelle, d.h. eine Welle mit großer Amplitude und kleiner Wellenlänge.
5.6 Reflexion mechanischer Wellen
Bei der Reflexion einer Welle muss man unterscheiden, ob die Welle an einem festen oder an einem losen Ende des Wellenträgers reflektiert wird.
• Bei der Reflexion einer Welle am festen Ende des Wellenträgers tritt ein Phasensprung auf - aus einem Wellenberg wird ein Wellental und aus einem Wellental ein Wellenberg.
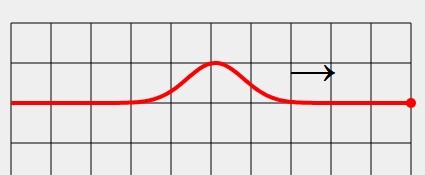
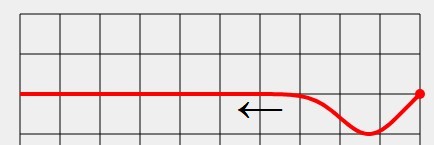
• Bei der Reflexion einer Welle am losen Ende des Wellenträgers tritt kein Phasensprung auf - ein Wellenberg bleibt ein Wellenberg und ein Wellental ein Wellental.
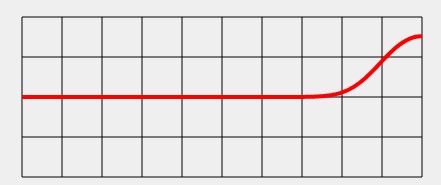
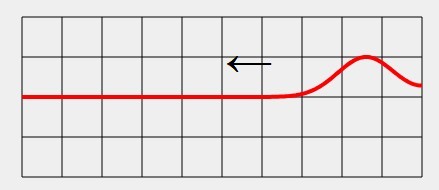
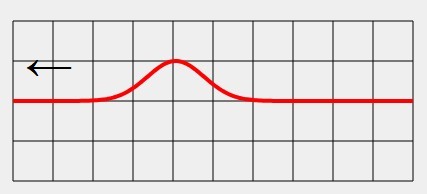
Siehe LEIF
5.7 Stehende Wellen
•Stehende Wellen können bei Überlagerung von zwei Wellen gleicher Frequenz und gleicher Amplitude entstehen.
•Bei stehenden Wellen bilden sich Knoten (keine Auslenkung) und Bäuche (maximale Auslenkung im Vergleich zur Umgebung) aus.
•Der Abstand zwischen zwei Knoten bzw. Bäuchen beträgt λ/2 der sich überlagernden Wellen.
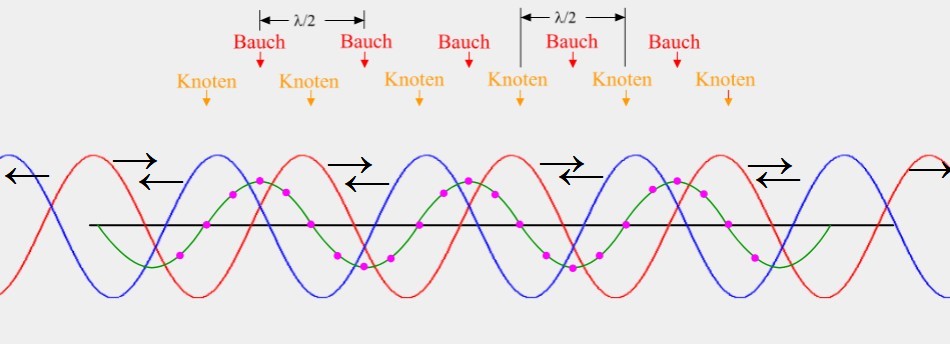
Die "rote" Welle wandert nach rechts, die "blaue" nach links. Sichtbar ist die "grüne" Welle.
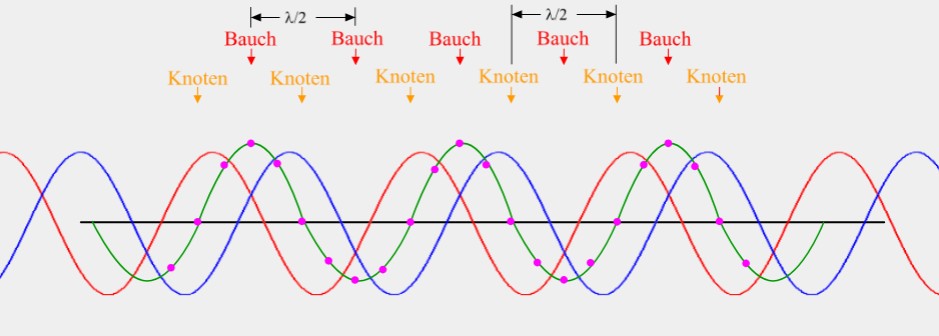
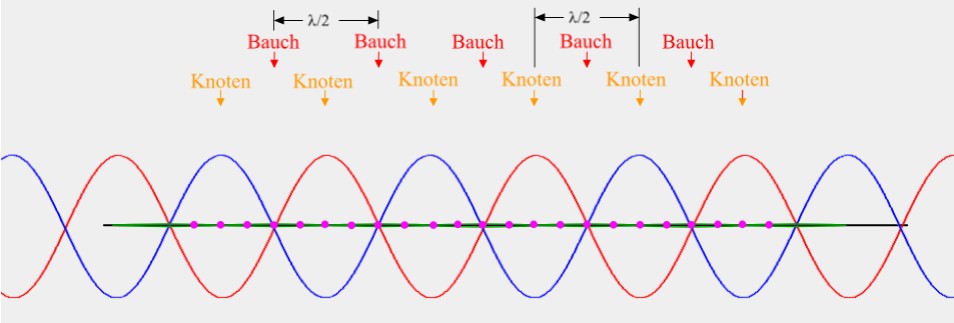
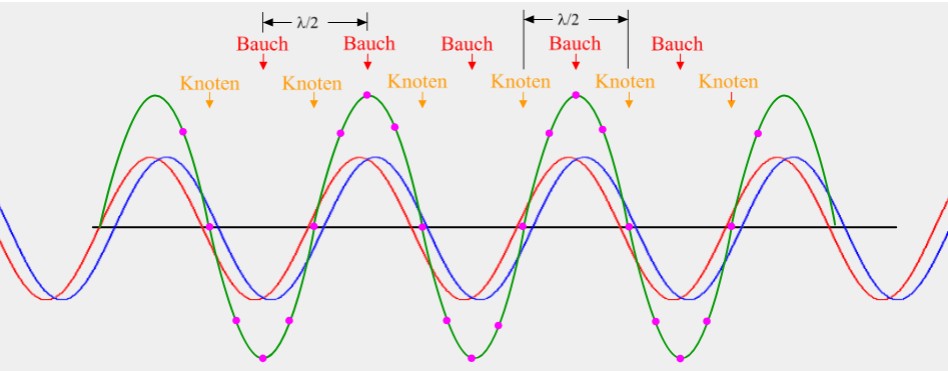
Siehe LEIF
5.8 Eigenschwingung und Resonanz
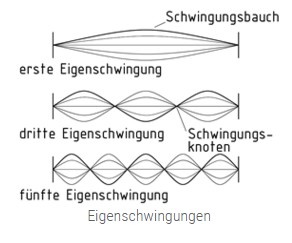Eine Eigenschwingung ist die Schwingung eines sich selbst überlassenen schwingungsfähigen Systems (z. B. Schwingkreis, Pendel, Saite der Geige) nach einer einmaligen Anregung. Meist werden neben einer Grundschwingung bestimmter Frequenz auch Oberschwingungen dieser Eigenschwingung angeregt. Eine Eigenschwingung - z.B. beim Monochord - tritt nur auf, wenn die Läge l ein Vielfaches der halben Wellenlänge ist l=n*λ/2.
Wird an einem Ende das Sytem angeregt, so breitet sich die Schwingung mit der Geschwindigkeit
c=λ/T aus.
Stehende Wellen bei einem Welleträger der Länge l=(2n+1)*λ/4.
Nie im Gleichschritt über eine Brücke, denn es könnte durch Eigenschwingungen zur Resonanzkatastrophe kommen.
5.9 Der Dopplereffekt
Der Doppler-Effekt ist die zeitliche Stauchung bzw. Dehnung einer Welle durch die Veränderungen des Abstands zwischen Sender und Empfänger.
Man unterscheidet häufig, ob sich der Sender oder der Empfänger bewegt. Der andere ist zur Vereinfachung in Ruhe.
• Verkleinert sich der Abstand Sender-Empfänger so steigt die wahrgenommene Frequenz.
• Vergrößert sich der Abstand so sinkt die wahrgenommene Frequenz.
Drei Formeln sind wichtig. Siehe Buch S.158/159
Die Schwingungsrichtung uns Ausbreitungsrichtung ist dieselbe.
Beispiel: Schallwellen oder stockender Autoverkehr
Transwersalwellen
Schwingungen sind senkrecht zur Ausbreitungsrichtung.Beispiel: Seilwelle, Lichtwelle, La-Ola-Welle.
Transversalwellen sind Polarisierbar.
5.3 Beschreibung von Wellen
Ein Oszillator ist ein hin-und herschwingendes Teilchen. Die harmonische Welle ist eine Idealisierung der Beschreibung. Amplitude und Frequenz einer Welle sind konstant.5.4 Wellen in Gleichungen
Für dei Geschwindigkeit einer Welle gilt: c=λ·f, wobei λ die Wellenlänge und f die Freuquenz.Beispiel Schallwelle: Wellenlänge λ=5,5mm. Frequenz f=40,1kHz ⇒ c=λ·f=0,0085m*401001/s=341m/s.
Eine fortschreitende Sinuswelle hat die Gleichung
´` t x
s(x;t)=s ·sin(2π·(—-—))
T λ
5.5 Überlagerungen von Wellen
Die Interferenz beschreibt die Überlagerung von zwei oder mehr Wellen nach dem Superpositionsprinzip.Konstruktive Interferenz
Die Wellenberge der einen Welle trifft die Wellenberge der anderen Welle. Wellenberg fällt auf Welleberg, Wellental fällt auf Wellental. Es entsteht eine Welle mit gleicher Frequenz mit einer Amplitude, die die Summe der beiden Amplituden ist.Destruktive Interferenz
Wellenberg fällt auf Wellental, Wellental fällt auf Wellenberg. Bei gleicher Amplitude entsteht eine Auslöschung längs der gesamten Ausbreitungsrichtung.Anwendung: Kopfhörer, der die Außengeräusche löscht.
Trifft eine Meereswelle mit kleiner Amplitude und großer Wellenlänge auf Land, so entsteht eine Monsterwelle, d.h. eine Welle mit großer Amplitude und kleiner Wellenlänge.
5.6 Reflexion mechanischer Wellen
Bei der Reflexion einer Welle muss man unterscheiden, ob die Welle an einem festen oder an einem losen Ende des Wellenträgers reflektiert wird.• Bei der Reflexion einer Welle am festen Ende des Wellenträgers tritt ein Phasensprung auf - aus einem Wellenberg wird ein Wellental und aus einem Wellental ein Wellenberg.
• Bei der Reflexion einer Welle am losen Ende des Wellenträgers tritt kein Phasensprung auf - ein Wellenberg bleibt ein Wellenberg und ein Wellental ein Wellental.
Siehe LEIF
5.7 Stehende Wellen
•Stehende Wellen können bei Überlagerung von zwei Wellen gleicher Frequenz und gleicher Amplitude entstehen.•Bei stehenden Wellen bilden sich Knoten (keine Auslenkung) und Bäuche (maximale Auslenkung im Vergleich zur Umgebung) aus.
•Der Abstand zwischen zwei Knoten bzw. Bäuchen beträgt λ/2 der sich überlagernden Wellen.
Die "rote" Welle wandert nach rechts, die "blaue" nach links. Sichtbar ist die "grüne" Welle.
Siehe LEIF
5.8 Eigenschwingung und Resonanz
Eine Eigenschwingung ist die Schwingung eines sich selbst überlassenen schwingungsfähigen Systems (z. B. Schwingkreis, Pendel, Saite der Geige) nach einer einmaligen Anregung. Meist werden neben einer Grundschwingung bestimmter Frequenz auch Oberschwingungen dieser Eigenschwingung angeregt. Eine Eigenschwingung - z.B. beim Monochord - tritt nur auf, wenn die Läge l ein Vielfaches der halben Wellenlänge ist l=n*λ/2.
Wird an einem Ende das Sytem angeregt, so breitet sich die Schwingung mit der Geschwindigkeit
c=λ/T aus.
Stehende Wellen bei einem Welleträger der Länge l=(2n+1)*λ/4.
Nie im Gleichschritt über eine Brücke, denn es könnte durch Eigenschwingungen zur Resonanzkatastrophe kommen.
5.9 Der Dopplereffekt
Der Doppler-Effekt ist die zeitliche Stauchung bzw. Dehnung einer Welle durch die Veränderungen des Abstands zwischen Sender und Empfänger. Man unterscheidet häufig, ob sich der Sender oder der Empfänger bewegt. Der andere ist zur Vereinfachung in Ruhe.• Verkleinert sich der Abstand Sender-Empfänger so steigt die wahrgenommene Frequenz.
• Vergrößert sich der Abstand so sinkt die wahrgenommene Frequenz.
Drei Formeln sind wichtig. Siehe Buch S.158/159