Die Homepage von Joachim Mohr  
≡

4.1 Beschreibung mechanischer Schwingungen

schwingung Zwei Beispiele:
• Eine Uhrenpendel oder eine Schaukel schwingt hin und her.
• Ein Feder-Masse-Pendel schwingt hoch und nieder
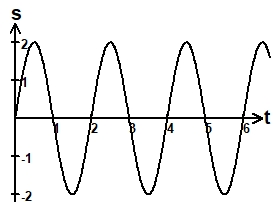
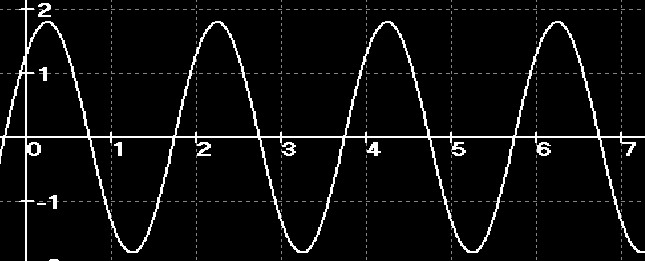
Ungedämpften Schwingungen sind harmonisch.

Hier im Schaubild ist die Schwingungsdauer T=2s und die Amplitude A=2cm.
Die Frequenz ist f=1/T, hier f=1/2Hz, wobei
1Hz=11/s.

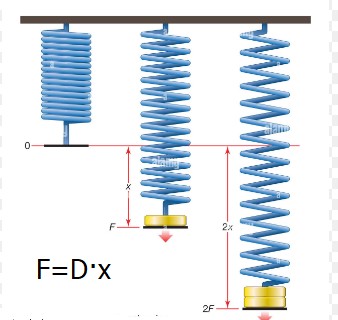
Hooksches Gesetz: F=D·x (D=Federkonstante)

Wird die Feder nicht überspannt, gilt das hooksche Gesetz:
Die Ausdehnung x ist probortional zur Kraft F.
D=20N/m, x=2cm ⇒ F=0,4N

4.2 Feder-Masse-Pendel induktiv

hook

F=D·x (D ist die Federkonstante)

Zwischen Federkonstante D, Masse m und Periodendauer T gilt: 
          —
         /m 
    T=2π√ —.
          D
Beispiel:
D=20N/m, m=200g ⇒ T=2π·√m/D=0,36s. (Hier Umrechnung Newton=N=kg·m/s2.)
Frequenz f=1,59Hz

4.3 Feder-Masse-Pendel deduktiv


Für den Bewegungsablauf eines Feder-Masse-Pendels gilt
einerseits F=-D*s(t), andererseits das Newtonsche Gesetz Kraft=Masse mal Bescheunigung F=m*a(t) 

         ..
Mit a(t)=s (t) (Zweite Ableitung) ergibt sich die DGL (Differentialgleichung)

 ..                                                            2              2π 
ms (t)=-D*s(t). Die DGL wird erfüllt von s(t)=A*sin(ωt) mit m*ω =D. Mit ω=2πf=—— folgt:
          —                                                                    T 
    1    /m
T=2π—=2π√ —. Also ist die Bewegungsgleichung s(t)=Asin(ωt).
    ω     D

4.4 Fadenpendel, U-Rohr, Federschwinger

                                                                      — 
                                                                     /l 
Ein Fadenpendel schwingt bei kleiner Auslenkung harmonisch mit  T=2π√ —
                                                                      g
Bei Vernachlässigung der Reibung schwingt dei Wassersäule im U-Rohr und der horizontale Federschwinger harmonisch.

4.5 Energie einer Schwingung

Satz: Bei einer ungedämpften Schwingung ist die Energie konstant gleich 
                   1   2  1   2
E   =E     +E    = —D*s + —m*v = konstant.
 ges  elong  kin   2      2

4.6 Zwei Schwingungen am selben Ort

Zwei Schwingungen mit derselben Frequenz:


s(t)=A1*sin(ω*t)+A2*sin(ω*t+φ0)
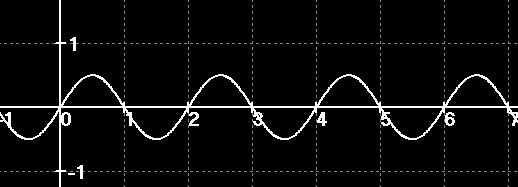
Beispiel: s(t)=1/2*sin(πx)
sin1
s(t)=3/2sin(πx+π/2)
sin2
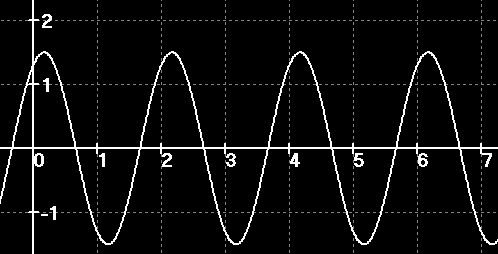
s(t)=1/2*sin(πx)+3/2sin(πx+π/2)=√10/2*sin(πx+arctan(3)) (mit ChatGPD gerechnet. Es ist richtig!)
sin2

Zwei Schwingungen mit 440Hz und 440,5Hz

440 anhören (Kammerton ohne Obrtöne)
440komma5 anhören (Etwas höher) 
←———————————————————————————————————————————————1/4Sekunde——————————————————————————————————————————————————→

440und440komma5 anhören (Mit Schwebungen)