3.1 Grundversuche zur Induktion

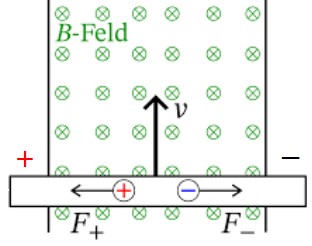
Wird ein elektrischer Leiter in einem Magnetfeld senkrecht zu den magnetischen Feldlinien bewegt, so wird eine Spannung in dem Leiter induziert.

Ursache ist die Lorentzkraft, die auf die frei beweglichen Elektronen im Leiter wirkt.
Die Linke Hand-Regel besagt:
Daumen: Bewegungsrichtung des Leiter (hier nach oben)
Zeigefinger: Richtung des Magnetfeldes (hier: nach hinten)
⇒Mittelfinger: Kaft auf Elektronen (hier nach rechts).
Dann ist der Pluspol des Leiters links.

Es wird also im Leiter eine Spannung U_ind induziert.
Die Spannung beträgt U_ind=B·v·d.

3.2 Induktion in Leiterschleifen

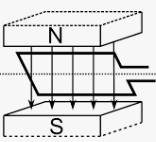Wird die Leiterschleife waagrecht von hinten nach vorne durch den Magneten gezogen, ereignet sich folgendes.
• Außerhalb: keine Spannung.
• Dann beim Hinenschieben: Die von den Feldlinien durchsetzte Fläche A vergrößert sich: Es wird eine Spannung induziert: U_ind=B·^ΔA/_Δt.
• Bewegung innerhalb des Magnetfeldes: U_ind=0V
• Bewegung aus Magnetfeld heraus: Spannung wird induziert, umgekehrt wie beim Hinenschieben.
• Dreht sich die Leiterschleife innerhalb des Magnetfeldes wird ein sinusförmiger Wechselstrom induziert.

Das Induktionsgesetz

Das Induktionsgesetz ist ein grundlegendes physikalisches Gesetz und die Grundlage für die Wirkungsweise solcher Geräte wie Transformatoren und Generatoren.
In einer Spule wird eine Spannung induziert, wenn sich das von der Spule umfasste Magnetfeld ändert.
Andererseits wird eine Spannung induziert, wenn sich die Leiterfläche A ändert.

         ΔB                        ΔA                    ΔΦ
U   =n*A*——  Andererseits U   =n*B*——. Also (s.u.) U   =n——, wobei Φ=B*A
 ind     Δt                ind     Δt               ind  Δt             S

Definition: magnetischer Fluß Φ=B*A_S, wobei A_S der senkrecht zu B stehende Teil der Fläche A ist. [Φ]=T*m²=V*s

3.3 Lenzsches Gesetz

Der Strom einer Induktonsspannung wirkt der Ursache der Induktion entgegen.
Begrundung: Energieerhaltungssatz.

                 . 
Deshalb: U   =-n*Φ(t)
          ind

3.4 Wirbelströme

Film

Eine Aluminiumscheibe schwingt zwischen den Polen eines Elektromagneten. Magnetfeld von rechts nach links,
a) Aluminiumscheibe ist geschlossen (ohne Schlitze): Sie wird sofort abgebremst.
b) Aluminiumscheibe mit Schlitzen: Wird nicht oder kaum abgebremst.
Erklärung: Fall a) Auf die mit der Platte sich bewegende Elektronen wirkt die Lorentzkraft. Sie fließen in einem Kreis. Das nennt man Wirbelströme. Die Wirbelströme wirken ihrer Ursache entgegen. Die Platte erwärmt sich (bei diesem kleinen Versuch wohl kaum nachweisbar). Umwandlung von Bewegungsenergie in Wärmeenergie.
b) Bei einer Platte mit Schlitzen können sich QWirbelströme kaum ausbilden. Die Platte wird nur wenig gebremst.
Bewegt sich eine Platte vollständig in einem Magnetfeld, werden keine Wirbelströme induziert.

3.5 Wechselspannung

Rotiert die Leiterschleife im Magnetfeld, so wird ein Wechselstrom erzeugt. Die Flussdichte ist konstant, der Flächenanteil senkrecht zu den magnetischen Feldlinien ändert sich.

               dA                  
U   = U   = -B*——. 
 ind   ind     dt               

Bei einer Spule mit n Windungen, ergibt sich U_ind=n*B*A*ω*sin(w*t), wobei ω=^2π/_T und T die Periodendauer.

Wechselstrom

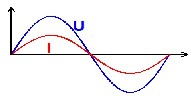
Im Wechselstromkreis sind Spannung und Stromstärke in Phase.

3.6 Selbstinduktion

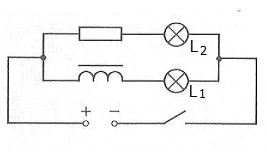Beim Einschalten leuchtet das Lämpchen L₂ verzögert auf

Selbstinduktion ist die Induktionswirkung eines Stromes auf seinen eigenen Leiterkreis Die Induktionsspannung U_ind ist proportional zur Änderungsrate des Stromes.

                  .                                                
Es gilt U    = -L*I, wobei L die Induktivität der Spule ist. 
         Ind                                                       
      Vs
[L]= 1—— = 1H (Henry). 
      A

Eine Induktivität von 1 H liegt vor, wenn bei gleichförmiger Stromänderung von 1 Ampere je Sekunde eine Selbstinduktionsspannung von 1 Volt entlang des Leiters entsteht.
Die Induktivität einer (lang gestreckten) Spule mit Querschnitt A und Länge l berechnet sich zu:

        n2*A 
L=μ *μ *————
   0  r   l

Beispiel: Eine luftgefüllte Spule (μ_r=1) hat n=600 Windungen. Die Länge beträgt 48mm, die Fläche 6,40cm². Die Induktivität berechnet sich zu:

                             -4 2
          -6 Vs 360000*6,4*10  m      Vs
L=1,257*10   ——*————————————————=0,006——=6mH
             Am   0,048m              A

3.7 Die Energie des Magnetfelds

Zu einer Spule mit Eisenkern wird eine Glühlampe parallel geschaltet. Das Lämpchen leuchte in einer mittleren Helligkeit. Öffnet man den Schalter, so leuchtet das Lämpchen kurzzeitig sehr hell auf. Die Energie muss aus dem Magnetfeld der Spule stammen.

Merke: Fließt durch eine Spule mit der Induktivität L ein Strom I, dann besitzt das Megnetfeld die Energie

      W_mag=¹/₂L*I²

3.8 Die Maxwellgleichungen

Zusammen mit der Lorentzkraft erklären die 4 Maxwellgleichungen alle Phänomene der klassischen Elektrodynamik.
James Clerk Maxwell hat sie von 1861 bis 1864 erarbeitet.

• Gaußsches Gesetz für elektrische Felder: Die Ladung ist Quelle des elektrischen Feldes.
• Gaußsches Gesetz für Magnetfelder: Das Feld der magnetischen Flussdichte ist quellenfrei; es gibt keine magnetischen Monopole.
• Faradaysche Induktionsgesetz: Änderungen des magnetischen Feldes führen zu einem elektrischen Wirbelfeld.
• Erweitertes ampéresches Gesetz: Elektrische Ströme und sich ändernde elektrische Felder führen zu einem magnetischen Wirbelfeld.

Die Maxwell-Gleichungen sind ein spezielles System von linearen partiellen Differentialgleichungen erster Ordnung.