2.1 Magnete und Magnetfeld

Hinweis: Bei der "technischen Stromrichtung" fließt der (gedachte) Strom von (+) nach (-). Dies ist eine Konvention früherer Zeiten und spiegelt nicht die tatsächliche Bewegung der Ladungen im Stromkreis. Tatsächlich fließen im Stromkreis die Elektronen vom -Pol zum +Pol.

Bei der Linken-Handregel weist der Daumen in Richtung des Elektronenflusses von (-) nach (+), bei der Rechten-Handregel der Daumen in Richtung der "technischen Stromrichtung" von (+) nach (-): 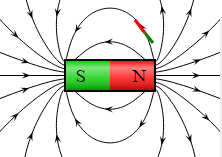Mangnete sind aus Eisen, Kobalt, Nickel oder elektrisch erzeugt.
Die Feldinien verlaufen vom Nordpol zu Südpol und geben die Kraftrichtung auf einen Nordpol an.
Eine Magnetnadel richtet sich entlang der Feldinien so aus, dass der Nordpol (hier rot) in Richtung der Feldinien zeigt.
Fließt ein Strom von + (hier links) nach - (hier rechts) so bildet sich ein Magnetfeld, dessen Feldlinien geschlossene Kreise um den Leiter bilden. Deren Feldlinien verlaufen hier vor dem Leiter von oben nach unten.
Rechte-Hand-Regel für den fließenden Strom (der fließt "gedacht" von + nach -), linke Hand-Regel für die fließenden Elektronen (Die fließen wirklich von - nach +).

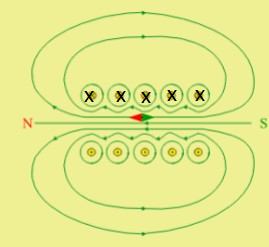
Magnetfeld einer stromdurchflossenen Spule

Der Strom fließt hier von (X) nach (∘) (technische Stromrichtung).
Also hinter dem Querschnitt hier nach unten).

Die magnetischen Feldlinien verlaufen in der Spule homogen von rechts nach links.

Außen ähnelt es dem Magnetfeld eines Stabmagneten.
Der magnetische Südpol der Spule ist hier rechts.

2.2 die Lorentzkraft

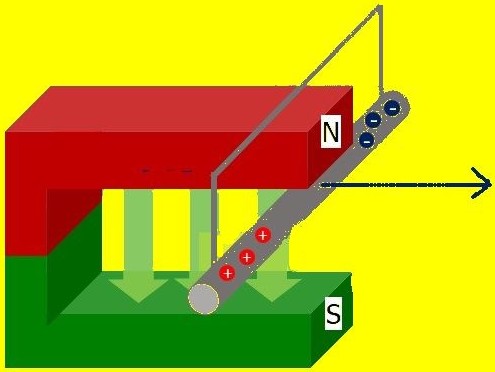Fließt im Leiter der Strom von (+) nach (-) und verlaufen die magnetischen Feldlinien senkrecht dazu von oben (Nord) nach unten (Süd), so wirkt auf den Leiter eine Kraft senkrecht zum Magnetfeld und senkrecht zur Stromrichtung. Die Richtung (nach rechts) wird mit Hilfe der Rechten-Hand-Regel ermittelt.

Die (magnetische) Lorentzkraft ist die die Kraft, die magnetische Felder auf bewegte Ladungen ausübt. Ihre Berechnung erfolgt über die magnetische Flussdichte.

2.3 Die magnetische Flussdichte

Die Kraft, die auf den stromdurchflossenen Leiter fließt ist proportional zur
      Stromstärke I und
      zur Länge des Leiters s.

Definition: Magnetische Flussdichte

     F                                N 
B = ——— mit der Einheit Tesla [B]=1T=1——
    I·s                               Am

          N   Vs       Nm
Beachte T=——=———, da V=——
          Am  2        As
             m

Seine Richtung ist dieselbe wie die der magnetischen Feldlinien. Für die Kraft gilt F=B*I*s.
Bewegen sich geladene Teilchen mit der Ladung q mit der Geschwindigkeit v im Magnetfeld, so ist mit

  q       s           q
I=— und v=— F=B*I*s=B*—*v*t=q*v*B
  t       t           t

Handelt es sich um ein Elektron mit der Ladung e, das sich im Magnetfeld mit der Flußdichte B bewegt, so wirkt auf es die Kraft

F=e*v*B

Für die Kraftrichtung gilt für negative Ladungen die Linke-Hand-Regel (Daumen: Bewegungsrichtung, Zeigefinger: magnetisches Feld, Mittelfinger: Kraft).
Die magnetische Flussdichte kann mit einer Hallsonde gemessen werden. Dabei ist die Flussdichte B proportional zur Hallspannung U_H.

U_H ∼ B

Die Flussdichte kann also mit Hilfe einer "kalibrierten" Hallsonde gemessen werden. "Kalibriert" heißt: Die Spannung der Hallsonde wird bei bekannter Flußdichte markiert. Auf ein Elektron, das sich mit der Geschwindigkeit v in einem magnetischen Feld mit der magnetischen Flußdichte B bewegt, wirkt die Kraft:
F=B·I·s=B·e·v, da I=Q/s, also hier I=e/s.

2.4 Die magnetische Feldkonstante

Elektromagnete enthalten Eisenkerne. Hier dagegen wird das Magnetfeld von im Innern mit Luft gefüllte Spulen betrachtet. Das Magnetfeld im Innern der Spule ist homogen. Die Flussdichte B∼H_H (∼ bedeutet: proportional) kann mit einer Hallsonde gemessen werden.

    n
Sei — =Anzahl der Windungen pro Längeneinheit,  
    l

(l die Länge der Spule) und I die Stromstärke, so ist

                     n                      -6 Vs
die Flussdichte B=μ ·—·I, wobei μ = 1,257·10   ——.
                   0 l           0             Am

Die magnetische Feldkonstante μ₀ hängt mit der elektrischen Feldkonstante ε₀ zusammen:

μ₀ε₀=¹/_c²

2.5 Das Magnetfeld verschiedener Spulen

Das Magnetfeld kurzer Spulen mit großem Durchmesser hat im Innern ein Maximum und fällt nach außen schnell ab.
Ist innerhalb der Spule ein ferromagnetischer Stoff, so erhöht sich die Flussdichte B=μ·B₀, wobei B₀ die Flussdichte ohne Kern ist. Die Permeabilitätszahl μ ist bei Eisen zwischen 300 und 10 000 (reine Zahlen).


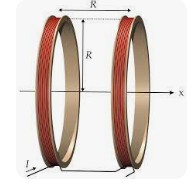
Zu erwähnen ist das Helmholtz-Spulenpaar. Fließt der Strom gleichinnig durch die Spulen entsteht ein homagenes Magnetfeld dazwischen.

2.6 Das Magnetfeld der Erde

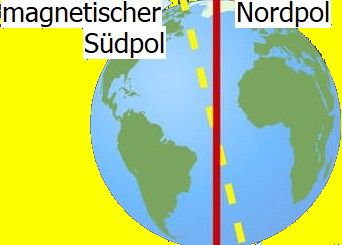Da der Nordpol der Kompassnadel nach Norden zeigt, ist der Nordpol der Erde der magnetische Südpol. Die Deklination (Abweichung vom genauen Nordpol) sind in Deutschland wenige Grade.
Die Inklination (Abweichung zur Waagrechten) ist in Stuttgart 65°, nach Norgen kleiner und nach Süden größer.

Das Magnetfeld der Erde schützt uns vor dem "Sonnenwind" (freien Elektronen und Atomkerne).

2.7 Elektronen im magnetischen Feld

Die Elektronenkanone EK emittiert in einem magnetischen Feld (hier senkrecht zum Bild nach hinten) Elektronen. Durch die Lorentzkraft werden die Elektronen auf eine Kreisbahn abgelenkt.
Die Lorentzkraft beträgt F_L=e·v·B. Dabei ist e die Ladung, v die Geschwindigkeit des Elektons und B die magnetische Flussdichte.
Die Lorentzkraft bewirkt als Zentripedalkraft F_L=F_Z=^m·v2/_r die Kreisbewegung.

          2
        mv                              mv
Aus evB=—— berechnet sich der Radius  r=——. 
        r                               eB

Die Energie ¹/₂mv², die ein Elekron durch die Elektronenkanone erhält ist, e*U. Daraus folgt

    ———
   /2eU 
v=√ ———
     m

Setzt man diese Gleichung in r ein, so erhält man (komplizierte Rechnung) die Spezifische Ladung des Elektrons

e    U                      e          11  C 
—=2————. Messungen ergaben  — = 1,76*10   ——
m   2 2                     m             kg
   B r

Nebenbei bemerkt: Die Masse des Elektrons ist m=9,109 383 7015*10^-31, also ca. 10³⁰ Elektronen haben die Masse von 1kg.

2.8 Massenspektrometer mit Geschwindigkeitsfiltern

Wienscher Geschwindigkeitsfilter

Ein Elektronenkanone schießt Elektronen in einen luftlehren Kolben. Sie werden abgelenkt durch ein magnetisches Feld. Gleichzeitig werden sie abgelenkt von einem Kondensator, der oben positiv und unten negativ geladen ist mit der Spannung U_K. Magnetfeld (von vorne nach hinten) und elektrisches Feld (von oben nach unten) stehen senkrecht aufeinander. Der Elektronenstrahl wird nach oben oder unten abgelenkt. Nun werden Magnetfeld und elektrisches Feld so austariert, dass sich die Ablenkungen aufheben. Der Elektronsnstrahl ist geradlinig.
Geschwindigkeit der Elektronen: v
Flußdichte des magnetischen Feldes: B
Elektrische Feldstärke E
Geradliniger Flug der Elektronen: q·v·B=q·E ⇒ v=^E/_B unabhängig von der ladung q und der Masse m.

---

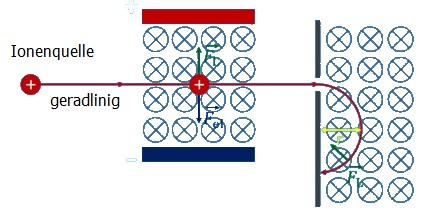Im Massenspektometer werden nach Durchtritt der Elektronen durch ein zweites Magnetfeld mit der Flußdichte B₂ auf eine Kreisbahn abgelenkt. In 2.7 sieht man r=^mv/_eB, hier also

  m v
r=—·—— Damit lässt sich die Masse m bestimmen.
  q B
     2