Die Homepage von Joachim Mohr
1.1 Elektrische Ladungen
1C = 1 Coulomb ≈ - Ladung von 6,24·1018 Elektronen (Elekronen sind neg. geladen)1C = 1As (Amperesekunde) 1A =1C/s.
Fließt eine Stunde 1 A, dann fließen 3600 C.
Elektrische Ladungen kann man mit dem Elektroskop nachweisen.
Die Elektronen sind negativ geladen. Die Protonen positiv.
Gleiche Ladungen stoßen sich ab. Deshalb gibt es einen Auschlag.
Im Bild stoßen sich die positiven Ladungen ab.
(Positive Ladungen bedeutet Elektronenmangel.)
Influenz bezeichnet die räumliche Verschiebung elektrischer Ladungen durch die Einwirkung eines elektrischen Feldes.
Auch bei nichtleitenden Materialien erfolgt durch Anlegen eines äußeren elektrischen Feldes eine Verschiebung von elektrischen Ladungen über kurze Distanzen in der Größenordnung eines Atomabstandes. (Der Abstand zweier Atome liegt in der Größenordnung 10−10m. Als Einheit wird oft Ångström mit 1 Å = 10-10 m = 0,1 nm verwendet.) Diesen Vorgang nennt man Polarisation.
Eisen ist ein leitendes Metall und besitzt daher frei bewegliche Elektronen. Wird ein geladener Gegenstand in die Nähe gebracht, entstehen bei Eisen Influenzladungen, bei Porzellan verformt sich nur die Atomhülle und es enteht ein Dipol.
Außer der elektrostatischen Kraft und der magnetischen Kraft gibt es bei Atomen noch die starke und schwache Wechselwirkung.
1.2 Kräfte zwischen Ladungen
elektrische Feldstärke = Kraft pro Ladung. E=F/q>
Zwischen den zwei verschieden geladenen Kondensatorplatten entsteht eine elektrisches Feld.
→ →
Auf eine Ladung dazwischen wirkt eine Kraft F=q·E,
→
wobei E die elektrische Feldstärke
N
ist Mit der Einheit [E]=1—
C
→ kN
Beispiel 1: Die Kraft in einem elektrischen Feld mit E =20 —— auf q=10nC
C
kN -9 3 -6
ist F = 10nC·20—— = 10·10 ·20·10 N =200·10 N = 200µN
C
Beispiel 2: Eine Ladung q=5nC erfährt eine Kraft von F=2mN. Wie stark ist das Elektrische Feld?
Aus F=q·E folgt E=F/q=2·10-3N/5·10-9C=0,4MN/C.
Das Coulombsche Gesetz
Auf zwei Ladungen q1 und q2 im Abstand r wirkt die Kraft
q ·q 2
1 2 1 -12 C
F=k·————— mit k=———— für ε = 8,85·10 ———
2 4πε 0 2
r 0 Nm
Zwei Ladungen mit q1=10-7C und q2=5·10-6C sind r=50cm voneinander entfernt.
Dann wirkt auf sie die Kraft:
2 -13 2
9 Nm 5·10 C
F=8,99·10 ————· ————————=17,9mN
2 2
C 0,25m
1.3 Das elektrische Feld
Ein elektrisches Feld bewirkt auf eine Probeladung q eine (elektrische) Kraft.Beispiel 1: Bei einem Gewitter herrscht zwischen Wolke und Erde ein elektrisches Feld.
Beispiel 2: Im Klassenzimmer kann man mit einem Bandgenerator elektrische Felder erzeugen.
Beispiel: Bei einem Gewitter betrage die Feldstärke zwischen Wolke und Erde
MN
E = 3,2——. Ein Wassertropfen trage die Ladung von q = 10nC.
C
Welche Kraft wirkt auf den Wassertropfen?
MN -9 6 N -3
Lösung: F = q·E = 10nC·3,2—— =10·10 C·3,2·10 — =32·10 N = 32mN.
C C
→
→ F
E = —
q
Die Feldstärke ist wie die Kraft ein Vektor.
Ist q negativ, dann ist die Feldstärke entgegengerichtet zur Kraft.
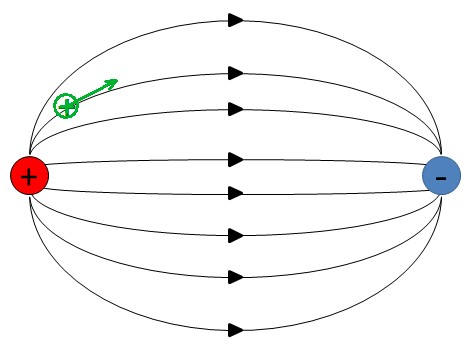
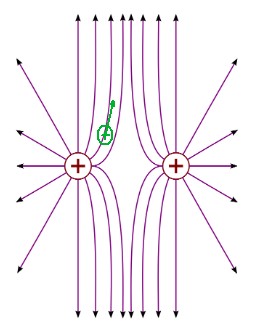
1.4 Feldlinienbilder
- Homogen beim Plattenkondensator
- Gekrümmt beim Dipol
Feldlinien verlaufen vom Pluspol zum Minuspol.
Feldlinien zeigen an, welche Kraft auf eine positive Ladung wirkt.
Auf negative Ladung wirkt die entgegengesetzte Kraft.
- Das Auto ist ein Faradayscher Käfig. Elektrische Feldlinien stehen senkrecht auf der Metalloberfläche.
In ihm ist man von Blitzen geschützt.
Wie entwickelt sich das elektrische Feld beim Gewitter?
Während sich die Gewitterwolke (Cumuluswolke) auftürmt, trennen sich in ihrem Innern die Ladungen durch Reibung, Stöße und Zerstäuben der Wasserteilchen: Die Eiskristalle laden sich positiv auf, die Tropfen negativ. Dadurch entsteht im kalten oberen Teil der Wolke ein Gebiet positiver Ladung, während nahe dem Erdboden negative Ladung überwiegt.1.5 Homogene elektrische Felder - Spannung
Elektrische Spannung
Das Wichtigste auf einen Blick- Als Spannung bezeichnet man die Fähigkeit einer elektrischen Quelle, in einem Stromkreis einen Strom aufrechtzuerhalten.
- Im Modell des offenen Wasserkreislaufs entspricht die Spannung dem Höhenunterschied der Vorratsbehälter.
- Die elektrische Spannung hat das Formelzeichen U und wird in der Einheit [U]=V (Volt) angegeben.
Zwischen A und B wirkt eine Feldstärke von E=4kN/C.
In A befindet sich eine Ladung von q=2nC.
Auf q wirkt die Kraft von F=q·E=8μN.
B ist von A d=5cm entfernt.
Die Ladung wird nach B tansportiert.
Dabei wird die Arbeit W = d·F =0,05m·8μN=4·10-7 Nm = 4·10-7 J verrichtet.
Die Spannung U zwischen A und B wird angegeben als Arbeit W=EEl pro Ladung für den Transport der Ladung q von A nach B.
Das Potential φ(P) eines Punktes P ist die Energie pro Ladung, um die Ladung vom einem Bezugspunkt P0 mit φ(P0)=0 zu P zu transportieren. Im Plattenkondensator kann man die negativ geladene Platte als Bezugspunkt wählen.
Die Spannung zwischen zwei Punkten A und B ist dann die Potentialdifferenz: U= φ(B)-φ(A).
el. Energie W Spannung U
Spannung = ———————————, U = — El. Feldstärke = ————————, E = —.
Ladung q Abstand d
Joule Newton·Meter J Nm
1 Volt = 1 ——————— = 1 ——————————————, 1 V = 1— = 1——
Coulomb Ampere·Sekunde C As
Aufgabe: Zwei Kondensatorplatten sind 2,2cm auseinander. An ihnen liegt eine Spannung von 220V.
(1) Wie groß ist die Feldstärke zwischen den Platten?
(2) Welche Arbeir wird verrichtet, wenn eine Ladung von 2nC von der einen Plattenseite auf die andere transportiert wird?
(1) Wie groß ist die Feldstärke zwischen den Platten?
(2) Welche Arbeir wird verrichtet, wenn eine Ladung von 2nC von der einen Plattenseite auf die andere transportiert wird?
U 220V kV
Lösung: (1) Aus U=E·d folgt: E=—= ————— = 10 ——
d 0,022m m
-9 J -9
(2) Verrichtete Arbeit W=q·U=2·10 C·220V. Mit V=— folgt W=440nJ. (n=10 ).
C
1.6 Flächenladungsdichte und elektrische Feldkonstante
Q
Die Ladungsdichte σ = — gibt an, wie groß die Ladung Q pro Fläche A ist.
A
C
Ihre Einheit ist [σ] = —
m2
→
Die Feldstärke E ist proportional zur Flächenladungsdichte σ.
Proportinal heißt: es gibt eine Konstante ε0 so, dass σ=ε0·E.
2
-12 C
ε = 8,85·10 ———— ist die elektrisch Feldkonstante (Im Vakuum und in der Luft).
0 2
Nm
Nm
Sie ist eine universelle physikalische Konstante. Mit der Einheit Volt V = —— ist auch
C
C
ε = 8,85·10-12———.
0 Vm
Beispiele
1. Beispiel: Ein Plattenkondensator trägt die Ladung Q=20C und hat eine Fläche von A=10dm2.Dann beträgt die Flächenladungsdichte
Q 20C C
σ=—=—————=200———.
A 2 2
0,1m m
2. Beispiel: Auf einem Plattenkondensator mit einer Fläche von 10dm2 befindet sich die Ladung von Q=10nC.
Die Flächenladungsdichte beträgt dann
Q 10nC -7 C
σ=—=—————=10 ——.
A 2 2
0,1m m
σ kN
Die elektrische Feldstärke ist dann E=——=11,3——
ε C
0
3.Beispiel: Die Platten eines Plattenkondensators haben je die Fläche von A=10dm2. Ihr Abstand ist d=5 cm. An Ihnen wird eine Spannung von U=1kV gemessen.
Dann beträgt die Elektrische Feldstärke E = U/d= 1kV/5cm = 20 000V/m = 20 000 N/C.
Die Flächenladungsdichte ist dann
-12 C V -9 C
σ=ε E =8,85·10 ——·20 000— = 177·10 ———.
0 Vm m 2
m
-9 C 1 2
Die Ladung auf den Platten ist dann Q= σ·A=177·10 ——·——m =17,7nC.
2 10
m
4. Beispiel: Die Platte eine Plattenkondensators der Fläche 10dm2 trägt eine Ladung von 0,4nC. Im Plattenkondensator wird eine Feldstärke von 450 N/C gemessen. Bestimme aus diesen Werten die elektrische Feldkonstante ε0!
Lösung:
Q 0,4nC -9 C
Die Flächenldungsdichte ist σ=—=—————=4·10 ——.
A 0,1m2 m2
N
Die Feldstärke beträgt E=450 —. Aus σ=ε E folgt:
C 0
C
-9 —
σ 4·10 m2 C2
ε =—=————————— =8,89·10-12———.
0 E N Nm2
450——
C
Sie ist proportional zur Feldstärke: σ=ε0·E, wobei ε0 die elektrische Feldkonstante ist.
1.7 Der Kondensator als Ladungsspeicher

Die Kapazität C (engl.: Capacity) eines Kondensators, Fähigkeit die Ladung Q bei eine angelegten Spannung U zu speichern, ist definiert als
Q V
C=— mit [C]=—.
U C
Achtung: Kapazität C und Coulomb C nicht verwechseln!
Hier wird aus schreibtechnischen Gründen meist auf Schrägschrift für Größen verzichtet.
C Coulomb
Die Einheit der Kapazität C wird mit F=Farad bezeichnet. 1F=1—=1———————
V Volt
Die Kapazität gibt also an, wieviel Ladung auf eine Platte pro Volt Spannung passt.
Die Kapazität eines Kondensators wird durch ein passendes Dielektrikum beeinflusst.
Für die Parallelschaltung von Kondensatoren gilt:
Ersatzkapazität
C=C1+C2+C3
Für die in Reihe geschalteten Kondensatoren gilt:
Ersatzkapazität
1 1 1 1 — = —— + —— + —— C C1 C2 C3
Beispiel 1: ist C1=C2=C3=C4=100μF, so ist
1 1 1 1 1 1 — = ———— + ———— + ———— + ———— = ———— also C=25μF C 100μF 100μF 100μF 100μF 25μFBeispiel 2: ist C1=10μF, C2=15μF und C3=20μF, so ist
1 1 1 1 13
— = ———— + ———— + ———— = ————
C 10μF 15μF 20μF 60μF
60
also C=——μF=4,62μF
13
1.8 Die Energie eines Kondensator
Die Energie eines Kondensator istW = EEl=1/2Q·U=1/2CU2=1/2Q2/C.
Die verschiedenen Darstellungen erfolgen aufgrund der Beziehung C=Q/U=Ladung pro Spannung.
Beispiel: Ein Kondensator hat die Kapazität von 200μF und wird mit 200V aufgeladen.
C=200μF=2·10-4C/V und U=200V
C=200μF=2·10-4C/V und U=200V
1 -4 C 2 J
W=E = —·2·10 —·40000V = 4C·V Mit V=— folgt: W=4J
el 2 V C
1.9 Auf- und Entladen eines Kondensators
Aufladen eines Kondensators
Wird eine Spannung im Stromkreis über den Wiederstand angeschlossen, so wird Ladung auf den Kondensator übertragen. Die Spannung steigt exponentiell von 0V bis U0.Der Strom, der fließt, fällt vom Maximalwert am Anfang exponentiell auf Null.
Stromstärke I=ΔQ/Δt = geflossene Ladung pro Zeit
1Ampere=1A=1C/s
Entladen eines Kondensators
Die Spannung am Kondensator ist U=Q/C.Ist der Schalter geschlossen, fließt Stom, die Ladung verringert sich.
Nach der Halbwertszeit T1/2 von z.B. 10s hat sich die Spannung halbiert,
Nach weiteren 10s ist sie nur noch zu 1/4 vorhanden usw.
t
———— Bei U =128V und T =10s entwickelt sich die Spannung folgendermaßen
T 0 1/2
1 1/2
U(t)=U ·(—) T in s| 10|20|30|40|50|60|70|80|90 |100|110|120 |...
0 2 ————————————————————————————————————————————————————————————————————————
U in V|128|64|32|16|8 | 4| 2| 1|1/2|1/4|1/8|1/16|—→0
Die Habwertszeit T1/2 hängt vom Widerstand R ab: T1/2 =R·C·ln(2).
Bei einer Kapazität des Kondensators von C=100µF=10-4C/V und einem Widerstand von 100kΩ=105V/A=105Vs/C
ist die Halbwertszeit T1/2= 1/2·105Vs/C·10-4C/V=5s.
Sie ist proportional zur Feldstärke: σ=ε0·E, wobei ε0 die elektrische Feldkonstante ist.
1.10 Bestimmung der Elementarladung/Millikan-Versuch
Prinzip des Millikanversuches
Zwischen zwei Kondensatorplatten schwebt ein Öltröpchen mit einer gewissen Laung q.Im elektrischen Feld des Kondensators wirkt auf das Tröpchen eine Kaft F↑ nach oben.
Andererseits wirkt die Gewichtskraft F↓ nach unten. Die Spannung wird so gewählt, dass das Tröpfchen schwebt.
Dann ist F↑=F↓ ist.
Rechnung:F↑=q·E mit der elektrischen Feldstärke E=U/d mit dem Platztenabstand d.
Die Gewichtskraft F↓ wird durch die Sinkgeschwindigelt des Tröpfchen ohne elektrischen Feld bestimmt (Komplizierte Rechnung!).
Man kann dann die Ladung q bestimmen. Es stellt sich heraus: Sie sind immer ein Viefaches von e.
Die Elementarladung berechnet sich zu e=1,602·10-19C.
1.11 Geladene Teilchen im elektrischen Feld
Die Elektronenkanone
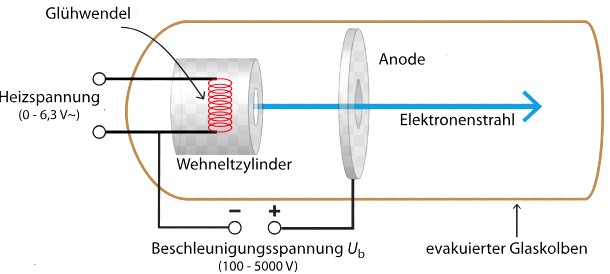
Zwischen Kathode(-) und Anode(+) weird eine Spannung angelegt.
Glühelektrischer Effekt
Wird die Glühkathode sehr heiß, treten Elekronen aus und werden im elektrischen Feld zwischen Kathode und Anode beschleunigt.
1. Beispiel: Auf welche Geschwindigkeit wird eine Elektron (Ladung e=1,6·10-19 C, Masse m=9,1·10-31kg bei einer Spannung von U=100V beschleunigt?
Lösung: Die kinetische Energie des Elektrons ist dann Wkin=1/2m·v2.
Für die Spannung U=100V gilt: U=W/q ("Arbeit pro Ladung"; hier q=e).
Also ist die kinetische Energie, die das Elekton durch das elektrische Feld erhält: Wel=U·e.
Aus Wkin=1/2m·v2=Wel=U·e folgt:
Elektronenvolt mit 1eV=1,6·10-19J (Genau: 1,602 176 634 x 10-19 J)
In unserem Beispiel mit 100V hat das Elekron die Energie von 160eV.
2. Beispiel: Ein Elektron hat nach einer Beschleunigung die Energie von 285eV.
Welche Geschwindigkeit hat es dann?
Lösung: Die kinetische Energie des Elektrons ist dann Wkin=1/2m·v2.
Für die Spannung U=100V gilt: U=W/q ("Arbeit pro Ladung"; hier q=e).
Also ist die kinetische Energie, die das Elekton durch das elektrische Feld erhält: Wel=U·e.
Aus Wkin=1/2m·v2=Wel=U·e folgt:
————
/2eU km km
V=\/————=6000——. Zum Vergleich Lichtgeschwindigkeit 300 000——.
m s s
Die Masse nimmt nach der Relativitätstheorie zu:
-31 km
Ruhemasse des Elektrons m=9,1·10 kg. Masse bei einer Geschwindikeit von v=6000——.
s
m -31
m = ——————————— =9,102·10 kg. Die Masse hat also um0,2% zugenommen.
rel ——————
/ 2
/ v
/ 1- ——
/ 2
\/ c
Die Energiemenge, die ein Elektron bei Beschleubigung in einem elekrischen Feld erfährt wird angegeben in:
Elektronenvolt mit 1eV=1,6·10-19J (Genau: 1,602 176 634 x 10-19 J)
In unserem Beispiel mit 100V hat das Elekron die Energie von 160eV.
2. Beispiel: Ein Elektron hat nach einer Beschleunigung die Energie von 285eV.
Welche Geschwindigkeit hat es dann?
2
1 2 -19 -19 kg·m
Lösung: Die kinetische Energie W=—m·v des Elektrons ist W=285eV=185·1,6·10 J=456·10 —————.
2 2
s
2 2
2 2W -31 2 2·456 -19+31 m 12 m
Daraus folgt: v = ——, wobei m=9,1·10 kg, also v = —————·10 —— = 100·10 ——,
m 9,1 2 2
s s
m 1
also v=10 000 000 — (etwa = —— der Lichtgeschwindigkeit).
s 30
1.12 Vergleich elektrisches Feld - Gravitationsfeld
Gewichtskraft FG=mg. Beispiel: g=3kg ⇒ FG=3kg·9,8N/kg=29,4N≈30N (Auf der Erde g≈9,8N/kg).Kraft im elektrischen Feld Fel=q·E. Beispiel: q=3C, E=10N/C ⇒Fel=3C·10N/C=30N. =·=·=·=·= Ende =·=·=·=·=
