Joachim Mohr Mathematik Musik Delphi
Das arithmetische Mittel im Vergleich zum geometrischen Mittel
oder
Das Quadrat ist unter den Rechtecken mit gleichem Umfang das mit dem größten Flächeninhalt.
Definition: Für zwei reelle Zahlen a und b ist
a + b
das arithmetische Mittel ————— und
2
———
das geometrische Mittel \/a·b (a,b > 0).
Satz: Das geometrische Mittel ist kleiner als das arithmetische oder gleich:
——— a + b
\/a·b ≤ ————— (*)
2
Bemerkung: Diesen Satz kann man verallgemeinern. Siehe
hier.Beweis: Die Idee ist folgende: Unter den Rechtecken mit gleichem Umfang hat das Quadrat den größten Flächeninhalt.
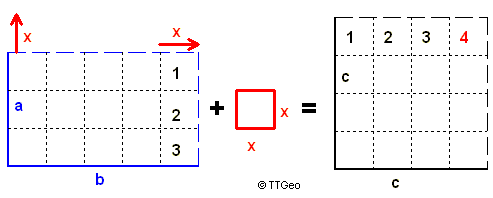
a + b
c = —————
2
2
a·b ≤ c
Ohne Einschränkung sei b ≥ a. Wir verlängern a bis c um den gleichen Betrag x wie wir b verkürzen bis c und erhalten dadurch ein Quadrat, dessen Flächeninhalt kleiner als jener des Rechtecks ist.
b - a
Die Rechnung dazu: a + x = b - x => x = —————
2
a + b
a + x = c und b - x = c => c = —————.
2
Die Zeichnung zeigt: Der Flächeninhalt des Rechtecks ist kleiner als der
Flächeninhalt des Quadrats (gleich nur, falls a = b).
Die Rechnung dazu: a·b + x^2 = (c - x) ·(c + x) + x ^2 = c^2 - x^2 + x^2
a + b 2 ——— a+b
Somit: a·b ≤ (—————) d.h. \/a·b ≤ ——— (a,b ≥ 0).
2 2
∎
Folgerung: Hat ein Rechteck
denselben Umfang wie ein Quadrat, so ist sein Flächeninhalt kleiner oder gleich der des Quadrats.
2
Als Ungleichung geschrieben: 2a + 2b = 4c => a·b ≤ c
2
Etwas vereinfacht: a + b = 2c => a·b ≤ c (a,b,c ≥ 0)
a+b
Beweis: Sei a + b = 2c. Dann ist ——— = c und es folgt aus
2
——— a+b 2
\/a·b ≤ (———) = c eben a·b ≤ c .
2
Ein rein algebraischer Beweis für die Ungleichung (*)
——— a+b
\/a·b ≤ ——— beide Seiten mit 2 multiplizieren!
2
——
⇔ 2\/a·b ≤ a+b beide Seiten quadrieren!
2
⇔ 4a·b ≤ (a+b) (Zu "⇐": Wurzel ist hier für a,b > 0 eindeutig)
2 2
⇔ 4a·b ≤ a + 2ab + b auf beiden Seiten 4a·b abziehen!
2 2
⇔ 0 ≤ a - 2ab + b
2
⇔ 0 ≤ (a-b)
Da die letzte Ungleichung offensichtlich allgemeingültig ist, ist auch die
die erste - äquivalente - Gleichung allgemeingültig.
Eine schöne Illustration ist der Beweis der Ungleichung (*) über die Logarithmusfunktion
Definition: Eine Funktion x → f(x) heißt konkav, wenn x → f'(x) monoton fallend ist,
d.h. wenn die Tangentensteigungen f'(x) mit wachsendem x kleiner werden.
Hier deutlich von "plus" über "Null" (waagrechte Tangente) zu "minus".
In diesem Fall ist f''(x) ≤ 0 für alle x im Definitionsbereich.
Geometrisch bedeutet dies: Das Schaubild beschreibt eine Rechtskurve.
Analog: konvex, f'(x) monoton wachsend, Linkskurve, f''(x) ≥ 0
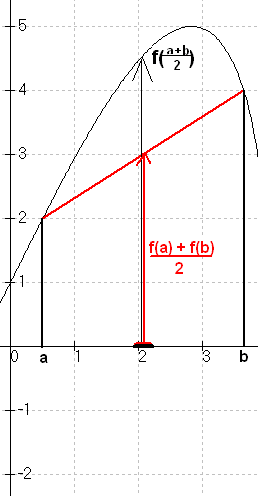
Satz: Für jede konkave Funktion f und
für alle a, b aus dem Definitionsbereich von f gilt:
f(a)+f(b) a+b
———————— ≤ f(———) (*)
2 2
d.h. der Funktionswert des Mittelwertes ist kleiner oder gleich dem Mittelwert der Funktionswerte.
Allgemeiner: Jede Sehne von A(a|f(a)) nach B(b|f(b))
verläuft unterhalb der Kurve.
x a b - a
Die Parameterform der Sehne ist: ( ) = ( ) + t( ) (0 ≤ t <1)
y f(a) f(b)-f(a)
Die Sehne liegt unterhalb der Kurve, wenn gilt:
y ≤ f(x),
f(a) + t(f(b) - f(a)) ≤ f(a + t(b-a)) oder
(1-t)f(a) + tf(b) ≤ f((1-t)a + tb) (0 ≤ t ≤ 1) (**)
Johann Jensen zeigte 1905: Für stetige Funktionen sind die Bedingungen
(*) und (**) gleichwertig.
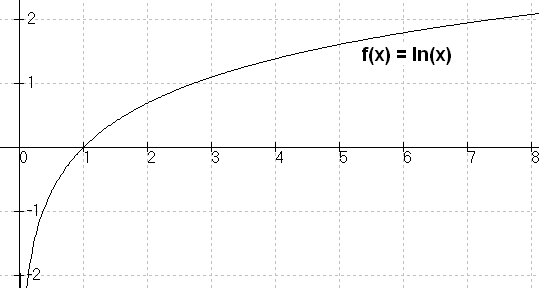
f(x) = ln(x)
1
f'(x) = -
x
1
f''(x) = - —— < 0
2
x
x → ln(x) ist konkav
——— a + b
Beweis der Ungleichung (*) \/a·b ≤ ————— :
2
Da die Funktion f: x → ln(x) konkav ist, gilt:
f(a) + f(b) a+b
———— ———— ≤ f(———)
2 2 2
ln(a) ln(b) a+b
———— + ———— ≤ ln(———)
2 2 2
x
Beide Gleichungen in die streng monoton steigende Funktion x → e eingesetzt:
ln(a) ln(b) a+b
———— + ———— ln(———)
2 2 2
e ≤ e
x
Die Gesetzte über die Exponentialfunktion x→e und ihrer Umkehrfunktion x→ln(x)
ln(p) 1 1
————— - -
ln(p) p+q p q 2 ln(p) 2 2 -
angewand (NB e = p und e = e ·e und e = (e ) = p = \/p ):
ln(a) ln(b) a+b
———— ———— ln(———)
2 2 2 - - a+b ——— a+b
e ·e ≤ e => \/a·\/b ≤ ——— => \/a·b ≤ ———.
2 2
∎
Die Verallgemeinerung des Satzes lautet:
x + x + x + ... x
n —————————————— 1 2 3 n
\/x ·x ·x ...·x ≤ ——————————————————
1 2 3 n n
Beweis
Weitere Mittelwerte: siehe "Ungleichungen", Zusammengestellt von Wolfgang Kirschenhofer (PDF)
