Die Messung von Stimmungen
Wir betrachten hier die Größe der Intervalle, nicht die Frequenzverhältnissen, die bekanntlich exponentiell wachsen. Zum Beispiel:
| Intervall | Frequenzverhältnis | Intervall | Frequenzverhältnis |
|---|---|---|---|
| 1 Ok = 1200 Cent | 2/1 | 1 Quinte = 702 Cent |
3/2 |
| 2 Ok = 2400 Cent | 4/1 | 2 Quinten = 1404 Cent | 9/4 |
| 3 Ok = 3600 Cent | 8/1 | 3 Quinten = 2106 Cent | 27/8 |
| 4 Ok = 4800 Cent | 16/1 | 4 Quinten = 2808 Cent | 81/16 |
| 5 Ok = 6000 Cent | 32/1 | 5 Quinten = 3510 Cent | 243/32 |
gleichstufig und pythagoreisch
Wir rechnen mit p = 1/12 pythagoreisches Komma:
p = Unterschied zwischen reiner und gleichstufiger Quinte
p = reine Quinte - 700 Cent = reine Quinte - 7/12Ok ≈ 2 Cent.
Genau:
12
3
1200•lb(———)
19 12
pythagoreisches Komma 2 3
p = ————————————————————— = ———————————— Cent = 100•lb(———) Cent ≈ 2 Cent
12 12 19
2
log(x)
mit lb(x) = log2(x) = ——————
log(2)
Dann erhalten wir für die Halbtöne unserer Klaviertastatur:
gleichstufig
c = 0 cis = 100 Cent d = 200 Cent es = 300 Cent e = 400 Cent f = 500 Cent fis = 600 Cent g = 700 Cent gis = 800 Cent a = 900 Cent b = 1000 Cent h = 1100 Cent c= 1200 Cent |
pythagoreisch:
c = 0 cis = 100Cent+7p d = 200Cent+2p es = 300Cent-3p e = 400Cent+4p f = 500Cent-p fis = 600Cent+6p g = 700Cent+p gis = 800Cent+8p a = 900Cent+3p b = 1000Cent-2p h = 1100Cent+5p c= 1200 Cent |
pythagoreisch in Cent
c = 0 cis = 114 Cent d = 204 Cent es = 294 Cent e = 408 Cent f = 498 Cent fis = 612 Cent g = 702 Cent gis = 816 Cent a = 906 Cent b = 996 Cent h = 1110 Cent c= 1200 Cent |
Die Skala ergänzt um enharmonische Töne (p ≈ 2 Cent).
Gleichstufig pythagoreisch pythagoreisch enharmonisch 000 Cent c=0 his=12p 100 Cent cis=100 Cent+7p des=100 Cent-5p 200 Cent d=200 Cent+2p eses=200 Cent-10p 300 Cent dis=300 Cent+9p es=300 Cent-3p 400 Cent e=400 Cent+4p fes=400 Cent-8p 500 Cent f=500 Cent-p eis=500 Cent+11p 600 Cent fis=600 Cent+6p ges=600 Cent-6p 700 Cent g=700 Cent+p asas=700 Cent-11p 800 Cent gis=800 Cent+8p as=800 Cent-4p 900 Cent a=900 Cent+3p heses=900 Cent-9p 1000 Cent ais=100 Cent0+10p b=100 Cent0-2p 1100 Cent h=1100 Cent+5p ces=1100 Cent-7p 1200 Cent c=1200 Cent deses=1200 Cent-12pDie enharmonischen Töne unterscheiden sich um 12p = pythagoreisches Komma ≈ 23 Cent.
——————
Fußnote für Mathematiker
Berechnungen des Frequenzverhältnisses
Sind die Centwerte mit dem genauen Wert von p=1/12 pythagoreisches Komma angegeben, so lässt sich auch das Frequenzverhältnis des Intervalls genau berechnen:In den folgenden Rechnungen wird mit der Einheit der Oktave Ok = 1200 Cent gerechnet.
12 12
1 1 3 1 3
p=——pythagoreisches Komma=——1200lb(———)Cent = ——*lb(———) Ok
12 12 19 12 19
2 2
Berechnung des Frequenzverhältnisses q aus der Größe i
Allgemein errechnet sich das Frequenzverhältnis q aus der Größe i in Oktav- oder Centwerten:
i i
—— ————————
Ok 1200Cent
q = 2 = 2
Wir rechnen mit dem Frequenzverhältnis des Pythagoreischen Kommas
12
3 lb(pk)
pk = ——— (12 Quinten aufwärts, 7 Oktaven abwärts) mit p= ——————
19 12
2
Beispiel 1 Für die Quinte g = 700Cent+p = 7/12Ok+1/12*lb(pk)Ok folgt
7 1
——Ok + ——lb(pk)
12 12 1 1 1 1 1
——————————————— ——(7+lb(pk)) —— —— —— 12 ——
Ok 12 (7+lb(pk)) 12 7 12 7 12 3 12 3
q=2 = 2 = (2 ) = (2 *lb(pk)) = (2 *pk) = (———) = —
12 2
2
Beispiel 2:
1 1
Für fis= 600 Cent +6p = — Ok + —*lb(pk) Ok berechnet sich das Frequenzverhältnis zu
2 2
1
1 1 - 1 1
— + —lb(pk) 2 — 12 — 6
2 2 (1+lb(pk)) 2 3 2 3
q=2 = 2 =(2*pk) = (———) = (——) (6 Quinten, oktaviert)
18 9
2 2
Bleibt die Frage: Wann ist für
12
n*Ok + m*lb(pk)Ok 3
i = 100*nCent + m*p = ————————————————— für pk=——— und Ok = 1200 Cent
12 19
2
das Frequenzverhältnis q rational?
1
Für das Intervall i = ——(n+mlb(pk)Ok folgt für das Frequenzverhältnis:
12
1 1
1 12*m —— 12m —— m
(n+mlb(pk)^(——) n 3 12 3 12 3
q=2 12 = (2 * —————) = (——————) = ———————————
19*m 19m-n (19m-n)/12
2 2 2
q ist also rational, wenn sich 19m-n durch 12 teilen lässt.Dabei steht n=0,1,2,...,12 für die Halbtöne und m für Vielfache von 1/12 pyth. Komma) ≈ 2 Cent.
Mitteltönige Stimmung im Vergleich
zur gleichstufigen Stimmung
Hier werden im pythagoreischen Quintenzirkel ... f(500-p) c(0) g(700+p) d(200+2p) ... die Quinten um 1/4 syntonisches Komma verkleinert. Mit q=1/4syntonisches Komma - p = 3,4215715337913 Cent ergibt mit dem mitteltönige Quintenzirkel ... f(500+q) c(0) g(700-q) d(200-2q) ...:
Im folgenden schreibe wir 100 statt 100 Cent usw.| mitteltönig:
c(0) cis(100-7q) d(200-2q) es(300+3q) e(400-4q) f(500+q) fis(600-6q) g(700-q) gis(800-8q) a(900-3q) b(1000+2q) h(1100-5) c(1200) |
enharmonisch:
des(100+5q) dis(300-9q) ges(600+6q) as(800+4q) ais(1000-10q) c(1200) |
In Cent:
c(0) cis(76) des(117) d(193) es(310) dis(269) e(386) f(503) fis(579) ges(621) g(697) gis(773) as(814) a(890) b(1007) ais(966) h(1083) c(1200) |
Reine Stimmung im Vergleich
zur gleichstufigen Stimmung
Die C-Dur- und Molltonleiter in reiner Stimmung schreibt sich dann in Eulerschreibweise. Mit der Abkürzung
k = syntonisches Komma = 1200*lb(81/80) = 21,5 Cent und
p = pythagoreisches Komma/12 = 1,955 Cent
|
Rein
c(0) d(200+2p) 'es(300-3p+k) ,e(400+4p-k) f(500-p) g(700+p) 'as(800-4p+k) ,a(900+3p-k) 'b(1000-2p+k) ,h(1100+5p-k) c(1200) |
In Cent
c(0) d(204) 'es(316) ,e(386) f(498) g(702) 'as(8014) ,a(884) 'b(1018) ,h(1088) c(1200) |
Daraus errechnet sich in Cent (mit dem Frequenzverhältnis):
chromatischer Halbton 'es,e = 100Cent+7p-2k = 70,67 Cent (25/24)
diatonischer Halbton ,ef = 100-5p+k = 111,73 Cent (16/15)
kleiner Ganzton d,e = 200+2p-k =182,40 Cent (10/9)
großer Ganzton cd = 200Cent+2p = 203,91 Cent (9/8)
kleine Terz c'es = 300Cent-3p+k =315,64 Cent (6/5)
große Terz c,e = 400Cent+4p-k = 386,31 Cent (5/4)
Quarte cf = 500Cent-p = 498,04 Cent (4/3)
Tritonus f,h = 600Cent+6p-k = 590,22 Cent (45/32)
verminderte Quinte ,hf = 600Cent-6p+k = 609,78 Cent (64/45)
Quinte cg = 700Cent+p = 701,96 Cent (3/2)
kleine Sext c'as = 800Cent-4p+k =813,69 Cent (8/5)
große Sext c,a = 900Cent+3p-k =884,36 Cent (5/3)
große kleine Septime dc = 1000Cent-2p = 996,09 Cent (16/9)
kleine kleine Septime cb = 1000Cent-2p+k = 1017,60 Cent (9/5)
große Septime c,h = 1100Cent+5p-k = 1088,27 Cent (15/8)
Oktave cc' = 1200 Cent (2/1)
Berechnungsbeispiel
Melodie: Vom Himmel hoch, da komm ich her.
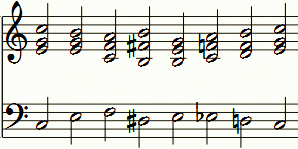
Es handelt sich hier um folgende Akkorde ohne Rücksicht auf die Oktavelage in Eulerschreibweise:
C-Dur c ,e g c
,e ,e g ,h
f c f ,a
e-Moll ,,dis ,h ,fis ,h
,e ,h ,e g
B-Dur es c f ,a
c-Dur d d f ,h
c ,e g c
Wie groß ist der Unterschied zwischen ,,dis und es?
In unserer Schreibweise berechnet sich das Intervall ,,dis es zu
,,dis(300+9p-2k)es(300-3p)
= -12p +2k = -pythagoreisches Komma + 2syntonisches Komma
= 19,55 Cent = Diaschisma (verminderte Sekunde).
