Fehler: in 000nav.txt ist nicht "gleichung4_alt.php" aufgeführt! Gleichung4_alt: Joachim Mohr Mathematik Musik Pascal Delphi
J o a c h i m   M o h r           Mathematik Musik Programmieren
≡

Veraltete Version

Gleichung 4. Grades
Zerlegung: x4+ax3+bx2+cx+d=(x2+px+q)(x2+sx+t)

Siehe auch Formel von Cardano       Gleichungen 4. Grades - Sonderfälle.

Eine schöne Darstellung von Ulrich Warnecke finden sie hier

Kurzfassung

Die Parameter p, q, s und t für der Zerlegung in quadratische Faktoren

x4+ax3+bx2+cx+d=(x2+px+q)(x2+sx+t)

berechnen sich folgendermaßen: (Lösungsformel von Joachim Mohr vom Mai 2009)

Maple-Programm

Formel von Joachim Mohr

   Bestimme eine Lösung u der Gleichung 3. Grades (Resolvente)

    3     2         2          2         2
   u - 2bu + (ac + b - 4d)u + c - abc + a d =0.

                                                               
   Falls a, b, c, d reell ist, gibt es ein reelles u 

              2
   mit 4u ≤ a 

                       ————
                      /2
   Dann ist mit w = \/a -4u

       a + w
   p = —————
         2

       (b-u)(w+a) - 2c
   q = ———————————————
            2w

       a - w
   s = —————
         2

       (b-u)(w-a) + 2c
   t = ———————————————
           2w
Kopierbar:
u^3+b1*u^2+b2*u+b3=0 für b1=-2*b b2=a*c+b^2-4*d b3=c^2-a*b*c+a^2*d
w=sqrt(a^2-4*u)
p=(a+w)/2
q=((b-u)*(w+a)-2*c)/(2*w)
s=(a-w)/2
t=((b-u)*(w-a)+2*c)/(2*w)
Bei reellen Koeffizienten a, b, c und d kann man die Rechnung im reellen Zahlenbereich (auch numerisch stabil) bewerkstelligen.
Beweisandeutung: Durch Ausmultiplizieren kommt man zu einer Resolvente 6. Ordnung, die sich jedoch zu einer Gleichung 3. Grades vereinfachen läßt.


Mir ist kein kürzeres Verfahren zur Lösung der Quartischen Gleichung bekannt.

Beispiel:

x4+6x3+18x2+30x+2=0 (a=6, b=18 c=30 d=25)

Rechnung:

Eine Lösung der Gleichung u3-36u2+404u-1440=0 ist u=8.
Daraus berechnen sich die Koeffizienten der beiden quadratischen Gleichungen:
w = sqrt(a2-4u) = 2
p = (a+w)/2 = 4
q = ((b-u)*(w+a)-2*c)/(2*w) = 5
s = (a-w)/2 = 2
t = ((b-u)*(w-a)+2*c)/(2*w) = 5

Die quadratischen Gleichungen x2 + px +q =0 und x2 + sx + t = 0 haben die Lösungen
x1 = -2 + i
x2 = -2 - i
x3 = -1 + 2i
x4 = -1 - 2i


Dies sind somit die Lösungen der Gleichung x4 + 6x3 + 18x2 + 30x + 25 = (x2 + 4x + 5)·(x2 + 2x + 5) = 0

Ausführlich

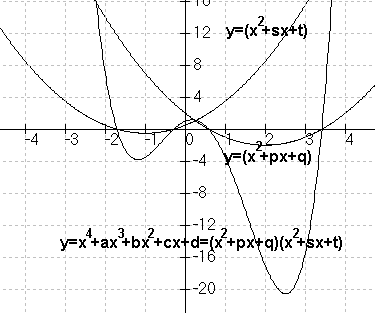
Polynom 4. Grades als Produkt zweier quadr. Polynome

Hier wird gezeigt wie man die quadratischen Teiler
g(x)=x2+px+q und
h(x)=x2+sx+t eines Polynoms
f(x)=x4+ax3+bx2+cx+d
mit Hilfe einer Lösung einer kubischen Gleichung berechnen kann.

x4+ax3+bx2+cx+d=(x2+px+q)(x2+sx+t)

Und damit hat man auch die Möglichkeit über die quadratische Gleichung die Nullstellen des Polynoms 4. Grades zu berechnen.

Nützlich ist dieses Verfahren vor allem für reelle Koeefizienten von a,b,c und d. Der Lösungsansatz ist jedoch auch für komplexe Koeefizienten denkbar. 

                      4    3    2                        
Dividiert man f(x) = x + ax + bx  + cx + d 
 
               2
durch g(x) = x   + px + q

so erhält man

f(x)=g(x)·h(x) + r(x), ausführlich

 4    3    2            2            2
x + ax + bx + cx +d = (x + px + q)·(x + sx + t) + r(x)

                                 2
mit s = a - p, t = b - q - ap + p  und

                   2   3                        
r(x) = (c - bp + ap - p - aq + 2pq)x 

                    2         2 
       + (d - bq + q + apq - p q)

Damit r(x)=0 wird, müssen wird also eine Lösung (p,q) des folgenden Gleichungssystems finden:

c-bp+ap2-p3-aq+2pq=0 (1)
d-bq+q2+apq-p2q=0 (2)

Wir lösen dieses Gleichungssystem aus zwei Gründen nicht nach dem Bairstow-Verfahren.
1. Iteration bei dem Bairstow-Verfahren ist zweidimensional.
2. Bairstow-Verfahren ist als zweidimensionales Newtonverfahren kritisch bei Extremwerten.
Die Lösung mit Hilfe der Cardanoformel wollen wir hier auch vermeiden, weil diese nicht - auch bei reellen Koeeffizienten a,b,c und d - mit reellen Zahlen bewerkstelligt werden kann.


Gleichung (1) nach q aufgelöst ergibt q=(p^3-ap^2+pb-c)/(2p-a)

Wird dies in die Gleichung (2) eingesetzt, kommt man auf die Gleichung 6. Grades, die sich aber mit Hilfe einer Gleichung 3. Grades lösen läßt.
p^6-3*a*p^5+(3*a^2+2*b)*p^4+(-a^3-4*b*a)*p^3+(c*a-4*d+b^2+2*b*a^2)*p^2 +(-b^2*a-a^2*c+4*d*a)*p+(-c^2+b*c*a-d*a^2)=0

Mit der Substitution u=p(a-p) vereinfacht sich diese Gleichung zu einer Gleichung 3. Grades, nämlich zu
u3 - 2bu2 + (ac + b2 - 4d)u + c2 - abc + a2d = 0
Kopierbar: u^3-2*b*u^2+(a*c+b^2-4*d)*u+c^2-a*b*c+a^2*d=0
u=p(a-p) nach p aufgelöst ergibt 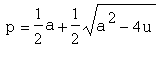p=1/2a+1/2*sqrt(a^2-4u)
Kopierbar: p=1/2*a+1/2*sqrt(a^2-4*u)
(Wähle dabei u so, dass a2≥4u, falls a, b, c und d reell.)

Probe mit Maple:
u:=p*a-p^2;
yp:=u^3-2*b*u^2+(c*a-4*d+b^2)*u+c^2-b*c*a+d*a^2;
y:=p^6-3*a*p^5+(3*a^2+2*b)*p^4+(-a^3-4*b*a)*p^3+(c*a-4*d+b^2+2*b*a^2)*p^2 +(-b^2*a-a^2*c+4*d*a)*p+(-c^2+b*c*a-d*a^2);
simplify(yp+y);#zeigt: yp=-y

Wir erhalten also für u mindestens eine reelle Lösung, die man mit geeigneten numerischen Verfahren (Newtonverfahren oder Intervallhalbierungsverfahren) lösen kann.

Hat man p bestimmt, so kann man q, s und t nach folgender Rechnung bestimmen:
q=(p^3-ap^2+pb-c)/(2p-a)
s=a-p und
t=b-q-a*p+p^2

Durch Umformulierung kommt man mit w=sqrt(a^2-4*u) auf:

p=(a+w)/2
q=((b-u)*(w+a)-2*c)/(2*w)
s=(a-w)/2
t=((b-u)*(w-a)+2*c)/(2*w)

Beispiel a)

f(x)=x4 + x3 + x2 + x + 1


führt auf die Gleichung u3 - 2u2 - 2u + 1 mit einer Lösung u = -1

Damit berechnet sich:
p=1/2+1/2*sqrt(5)
q=1
s=-1/2*sqrt(5)+1/2
t=1

x1=(-1/4-1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
x2=(-1/4-1/4*sqrt(5))+(sqrt(5/8-1/8*sqrt(5)))*i
x3=(1/4*sqrt(5)-1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
x4=(1/4*sqrt(5)-1/4)+(sqrt(1/8*sqrt(5)+5/8))*i
Somit f(x)=(x2+(-1/2*sqrt(5)+1/2)x+1)(x2+(1/2+1/2*sqrt(5))x+1)

Beispiel b)

f(x)=x4 - x3 + 2x2 - x + 1


führt auf die Gleichung u3 - 4u2 + u = 0 mit einer Lösung u = 0

Damit berechnet sich: p=0
q=1
s=-1
t=1

x1=i
x2=i
x3=1/2+1/2*sqrt(3)i
x4=1/2-1/2*sqrt(3)i

Somit f(x)=(x2-x+1)(x2+1)

Beispiel c)

f(x)=x4 - x3 + 2x2 - 3x + 1

führt auf die Gleichung
u3 - 4u2 + 3u + 4 = 0 mit einer Lösung u = -0,658967081916994102 
                        2               —————————
                      -w +4w-7        3/      ———
Der genaue Wert ist u=———————— mit  w=\/44+3\/177.
                        3w
Damit berechnet sich:

p=0,45339765151640378
q=2,20556943040059031
s=-1,45339765151640378
t=0,453397651516403796


x1=-0,226698825758201897 + 1,46771150871022426i
x2=-0,226698825758201896 - 1,46771150871022426i
x3=1
x4=0,453397651516403857

Somit
f(x)=(x2+0,453397651516x+2,205569430401)·(x2-1,453397651516x+0,453397651516)

Beispiel d)

f(x)=x4+2x3-14x2+2x+1


führt auf die Gleichung u3 - 28u2 + 196u + 64 = 0 mit einer Lösung u = -16
Damit berechnet sich:
p=1+sqrt(17)
q=1
s=1-sqrt(17)
t=1

Die Lösungen sind somit:

x1=1/2*sqrt(17)-1/2+1/2*sqrt(14-2*sqrt(17))
x2=1/2*sqrt(17)-1/2-1/2*sqrt(14-2*sqrt(17))
x3=-1/2-1/2*sqrt(17)+1/2*sqrt(14+2*sqrt(17))
x4=-1/2-1/2*sqrt(17)-1/2*sqrt(14+2*sqrt(17))


x1=2,76090563295441601
x2=0,362199992663244539
x3=-0,203258341626567109
x4=-4,91984728399109344

Beispiel e)

Für f(x)=x4+3x3-8x-6 (a=3, b=0, c=-8, d= -6) erhält man die Gleichung
z3+10 = 0 mit der Lösung u= -101/3.

Das Rechenschema liefert in diesem Fall die Werte:


p=(3+h)/2 = 3,598674508
q=(h*w+16+3*w)/(2*(9+4*w)^(1/2)) = 3,753109199
s=(3-h)/2 = -0,598674508
t=(h*w-16-3*w)/(2*h) = -1.598674508

mit w=10^(1/3) und h := sqrt(9+4*w)


x1 = -1,7993372539+I*0,7179795572
x2 = -1,7993372539+I*0,7179795572
x3 = 1,5986745079
x4 = -1

Beispiel f)

Für f(x)=16x4+8x3-16x2-8x+1 (a=1/2, b=-1, c=-1/2 und d=1/16) erhält man die Gleichung
z3+2z2+1/2z+1/64 = 0 mit der Lösung u= -1/4. Das Rechenschema liefert in diesem Fall die Werte:

p=1/4+1/4*sqrt(5)
q=-3/8+1/8*sqrt(5)
s=-1/4*sqrt(5)+1/4
t=-1/8*sqrt(5)-3/8


x1=1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))-(sqrt(5)+1)) = cos(84°)
x2=-1/8*(sqrt(2)*sqrt(3)*sqrt(5-sqrt(5))+(sqrt(5)+1)) = -cos(24°)
x3=1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))+(sqrt(5)-1)) = cos(12°)
x4=-1/8*(sqrt(2)*sqrt(3)*sqrt(5+sqrt(5))-(sqrt(5)-1)) = -cos(48°)
(Die Cosinuswerte finden sich in dieser Tabelle. Aber das ist ein anderes Thema.)