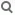Vertiefung zur vollständige Induktion
Im Folgenden sei N = {1, 2, 3, 4, ... } die Menge der natürlichen Zahlen.
Die vollständige Induktion ist eine Beweistechnik, um die Allgemeingültigkeit von Aussagenformen der Form A(n) (n ε N) zu beweisen.
I Der Schluss von n auf n+1
Beweisschema der
|
| Die Formel A(n) soll bewiesen werden. |
| Der Beweis erfolgt in zwei Schritten |
| I Induktionsanfang: Prüfe, ob A(1) wahr ist. |
| II Induktionsschritt: Zeige: A(n) =〉 A(n+1) (n ε N)
("Aus A(n) kann A(n+1) hergeleitet werden") |
Dieses ist das übliche Beweisschema, das auf Peano zurückgeht.
Viele Beispiele dazu sind im Crashkurs zur vollständigen Induktion zu finden.
Im Folgenden bringen wir einige Folgerungen (Beweise siehe unten).
II Die 1. mengentheoretische Formulierung
III Die 2. mengentheoretische Formulierung
Man sagt auch dazu: die Ordnung von N ist eine Wohlordnung.
IV Die starke vollständige Induktion
Den letzten Satz kann man wieder zu einem Beweisschema umformulieren.
Beweisschema der starken vollständigen Induktion |
| Die Formel A(n) soll bewiesen werden. |
| I Induktionsanfang: Prüfe, ob A(1) wahr ist. |
| Induktionsschritt:
Zeige: Wenn A(k) für alle k ≤ n gilt, dann gilt auch A(n+1) (n ε N) |
|
1
1 → 2 1,2 → 3 1,2,3 → 4 1,2,3,4 → 5 1,2,3,4,5 → 6 1,2,3,4,5,6 → 7 ... |
Ich darf hier im Induktionsschritt als Induktionsvoraussetzung nicht nur A(n) vorgeben sondern A(1), A(2), ..., A(n). Der Satz ist also "stärker" als die "normale" vollständige Induktion.
Diese Form des Induktionsprinzips wird gern verwendet, um zu zeigen, dass jede natürliche Zahl eine Primfaktorenzerlegung besitzt. (Siehe: Beweis)
Ein anderes Beispiel, bei dem diese Beweismethode Gebrauch findet, ist der erweiterte Euklidische Algorithmus.
Diesen Satz kann man auf Mengen mit einer Wohlordnung übertragen. Man nennt das Beweisschema dann "transfinite Induktion".
V Die Vorwärts-Rückwärtsmethode
Manchmal kann man nicht A(n+1) direkt aus A(n) herleiten, sondern über A(2n), A(2n-1), A(2n-2),...,A(n+1).
↓
2
↓
4→ 3
↓
8→ 7→ 6→ 5
↓
16→ 15→ 14→ 13→ 12→ 11→ 10→ 9
↓
32→ 31→ 30→ 29→ 28→ 27→ 26→ → 25→ 24→ 23→ 22→ 21→ 20→ 19→ 18→ 17
↓
...
Die Vorwärts-Rückwärtsmethode |
| Die Formel A(n) soll bewiesen werden. |
| I Induktionsanfang: Prüfe, ob A(1) wahr ist. |
| Induktionsschritt:
Zeige: Aus A(n) folgt A(2n) (n ε N) und: Aus A(n) folgt A(n-1) (n 〉1) |
Ein schönes Beispiel für die Anwendung ist der Beweis der Ungleichung für das geometrische und arithmetische Mittel.
Beweise
Voraussetzung: In unserem Rechenbereich N gelten die folgenden Peanoaxiome.
- 1 ist eine natürliche Zahl.
- Es gibt eine Nachfolgerfunktion, d.h. es gibt eine bijektive Abbildung n-〉n' von N auf N \ {1}.
- Es gilt das Induktionsprinzip I.
Gleichgültig, welches Induktionsprinzip verwendet wird, kann in einem solchen Rechenbereich eine Addition mit n' = n + 1 definiert werden (die Multiplikation benötigen wir in unseren Beweisen nicht) und eine Kleinerrelation "〈" mit n 〈 n+1 (wobei es kein k ε N gibt mit n 〈 k 〈 n+1).
Sei K eine Teilmenge von N mit 1 ε K und mit n ist auch n+1 ε K.
Wir zeigen mit Hilfe des Induktionsprinzips I, dass K = N ist.
Dazu betrachten wir die Aussageform A(n): n ε K.
Es gilt A(1) (da 1 ε K) und mit A(n) auch A(n+1) (da mit n ε K auch n+1 ε K ist).
Nach dem Induktionsprinzip I gilt A(n) für alle n ε N, also gilt:
Für alle n ε N ist n ε K. Somit K = N.
∎
I ist sogar gleichwertig mit
II. Wir zeigen deshalb auch:
Sei A(n) eine Aussage, für die A(1) und mit A(n) auch A(n+1) gilt.
Definiere K = {k ε N| A(k)}.
Dann gilt 1 ε K und mit n ε K ist auch n+1 ε K.
Nach
II ist K = N, also ist A(n) für alle n ε N gültig.
∎
Statt A(n): "n ist nicht in K" - was man wohl zunächst versuchen würde - definiert man
A(n): Alle k ≤ n sind nicht in K (Dank an Thomas Haunhorst in de.sci.mathematik).
Bei der ersten Definition kann es passieren, dass zwar n nicht in K aber ein k 〈 n doch in K nicht ausgeschlossen ist.
Sei K eine Teilmenge von N ohne kleinstes Element. Wir zeigen: Dann ist K die leere Menge.
Für jedes n ε N definieren wir A(n) als die Aussage: "Es gibt kein k ε K mit k ε n".
Anders formuliert bedeutet A(n): "Es gibt kein k ε K mit k in {1,2,3,...,n}" oder "K und {1,2,...,n} sind teilerfremd."
Dann gilt:
A(1). Denn gäbe es ein k ε K mit k ≤ 1, so wäre k = 1 kleinstes Element von K.
Setzen wir nun die Induktionsvoraussetzung A(n) (n ≥ 1) voraus, d.h. Es gibt kein k ε K mit k ≤ n.
Wir zeigen dann, dass auch A(n+1) gültig ist.
Nach Induktionsvorrasusetzung ist kein k ε K in der Menge {1,2,...,n}. Dann kann aber n+1 nicht in K liegen, sonst wäre es das kleinste Element von K. Also ist auch kein Element von K in {1,2,...,n+1}, d.h. es gilt auch A(n+1).
Nach dem Induktionsprinzip ist also für alle n ε N die Aussage A(n) gültig und somit kein n ε K.
Die Menge K ist die leere Menge.
∎
Auch III ist äquivalent zu II bzw. I. Wir beweisen deshalb auch:
Sei K eine Menge, die 1 und mit n auch n+1 (n ≥ 1) enthält. Wir zeigen mit Hilfe von
III, dass K = N ist.
Wir betrachten L = N \ K = {k ε N| nicht n ε K} die Komplementmenge von K.
Wäre L nicht leer, dann besäße L ein kleinstes Element n0.
n0 kann nicht 1 sein, da 1 ε K, dann ist also n0 - 1 ≥ 1 und n0 - 1 ε K = N \L.
Nach Induktionsvoraussetzung ist aber mit n0-1 auch n0εK, was nicht sein kann,
da nach unserer Annahme k ε L = N \ K ist.
Also ist L leer und K = N.
∎
Sei A(n) eine Formel mit folgender Eigenschaft:
Es gilt A(1) und wenn A(k) für alle k ≥ n gilt, dann gilt auch A(n+1) (n ε N).
Wir beweisen mit Hilfe von
III, dass A(n ) für alle n ε N gilt.
Setzte K = {n ε N| nicht A(n)}. Wir zeigen über einen Widerspruchsbeweis, dass K die leere Menge ist.
Nehmen wir an, K sei nicht leer. Dann besitzt nach
III K ein kleinstes Element n0 ε N.
Wegen A(1) ist n0 〉 1.
Für jedes n ε N mit n 〈 n0 gilt dann A(n). Aber dann gälte auch A(n0), was einen Widerspruch ergibt.
Auch IV ist äquivalent zu III (und damit auch zu I und II).
Beweis IV (starke vollständige Induktion)=〉 III (Wohnordnung von N):
Sei K eine Teilmenge von N ohne kleinstes Element.
Wir zeigen mit Hilfe von IV, dass K leer ist.
Wir betrachten die Aussage A(n): nicht n ε K:
Es gilt A(1), denn sonst wäre 1 kleinstes Element von K.
Wenn A(k) für k ≤ n gilt, d.h. wenn nicht 1 ε K, nicht 2 ε K, ..., nicht n ε K,
dann ist auch n+1 kein Element von K, sonst wäre es das kleinste in K.
Folglich gilt auch A(n+1).
Nach IV gilt A(n) für alle n ε N, also nicht n ε K für alle n ε N.
Damit ist bewiesen, dass K die leere Menge ist.
∎
Beweis III (Wohnordnung von N) =〉 V (Vorwärts-Rückwärtsmethode):
Sei A(n) eine Aussage, für die gilt:
- A(1)
- mit A(n) auch A(2n) (n ≥ 1) und
- mit A(n) auch A(n-1) (n 〉 1).
Wir zeigen mit Hilfe von III, dass A(n) für alle n ε N gilt.
Das heißt: Wir zeigen dass die Menge K = {n ε N| nicht A(n)} leer ist.
Wäre nämlich K nicht leer, dann hätte k nach III ein kleinstes Element n.
Dies ist wegen der Gültigkeit von A(1) nicht die "1".
n ist nicht gerade, da für n = 2k (k ε N, k 〈 n) A(k) gültig wäre
(n ist ja das kleinste Element mit nicht A(n)) und damit auch A(n) = A(2k) gültig wäre,
also nicht n ε K, folgern würde.
Nehmen wir nun an: n ist ungerade, etwa n =2k-1 ( k ε N, 1 〈 k 〈 n).
Aus A(k) folgt A(2k) und aus A(2k) folgt A(n) = A(2k-1), im Wiederspruch zu nicht A(n).
∎
Beispiel zu starken vollständigen Induktion.
Beweis:
Induktionsanfang: n=2 ist Primzahl
Induktionsschritt:
Sei bereits bewiesen, dass für alle k ≤ n eine Primfaktorenzerlegung existiert (n ≥ 2).
Wir müssen zeigen, dass n+1 eine Primfaktorenzerlegung besitzt.
Ist n+1 eine Primzahl, so sind wir fertig, im anderen Fall ist n=a·b (a, b ≥ 2).
Da a ≤ n und b ≤ n ist, besitzen beide eine Primfaktorenzerlegung und damit auch n+1.
∎