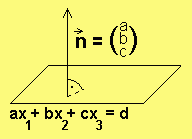Die Homepage von Joachim Mohr
Zurück
Einführung in das Skalarprodukt
in Aufgaben
Diese Datei kann auch als PDF-Datei heruntergeladen werden. Download ....Motivation aus der Physik
→
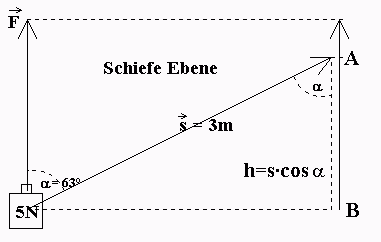
α = Winkel zwischen angreifender Kraft F und
→
zurückgelegtem Weg s
Mit dem Wechselwinkel ergibt sich:
Ankathete h
cos(α) = —————————— = - => h = s·cos(α)
Hypotenuse s
Antwort: Man kann den Körper auch zuerst nach B transportieren. Die aufzuwendende Arbeit ist 0 (Reibungskräfte werden vernachlässigt.). Anschließend wird er senkrecht nach oben mit dem Höhenunterschied h = s·cos(α) transportiert. Die aufzuwendende Arbeit ist dann
W = F·h = F·s·cos(α)
=5N·3m·cos(63°) = 6,81 Nm = 6,81 J
Genau diese Formel steckt in der Definition des
Skalarproduktes.Unabhängig vom physikalischen Bezug: Immer, wenn von Winkeln die Rede ist, benötigt man das Skalarprodukt.
Definition des Skalarprodukts
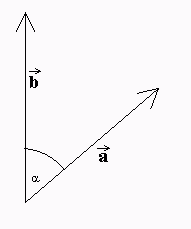
→ → a ·b = a·b·cos(α) = |a|·|b|·cos(α), → wobei a = |a| = Betrag von a, → b = |b| = Betrag von b und → → α = Winkel zwischen a und b ist.
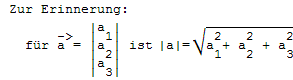
Beispiele: a = 5, b = 3, verschiedene Winkel.
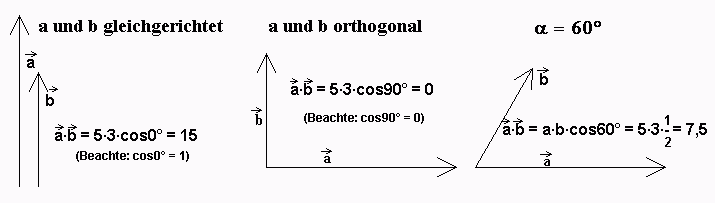
Man sieht: Das Skalarprodukt von zwei Vektoren ist eine reelle Zahl im Gegensatz zu einem Vektor. Der Physiker spricht dann von einer skalaren Größe im Gegensatz zu einer gerichteten Größe. Reine Zahlenwerte (Skalare) sind zum Beispiel die Lageenergie, die Zeit, die Temperatur und die elektrische Ladung, gerichtete Größen sind zum Beispiel die Geschwindigkeit, die Kraft oder die elektrische Feldstärke.
Ganz wichtig ist folgende einfache Tatsache:
Merke!
(Der 1. Hauptsatz für das Skalarprodukt)
a orthogonal b ⇔ a·b = 0
Nach dieser Beziehung ist der Nullvektor senkrecht zu jedem Vektor.
Für das Skalarprodukt gelten die üblichen Rechenregeln.
Regeln für das Skalarprodukt
KG
Das Kommutativgesetz:
→ → → → a ·b = b ·a
das ist offensichtlich
AG
Das gemischte Assoziativgesetz:
→ → → >
(k·a )·b = k·(a ·b )
für k e R
(k=2)
"doppeltes Gewicht => doppelte Arbeit"
DG
Das Distributivgesetz:
→ → → → → → → a ·(b + c ) = a ·b + a ·c
siehe untenstehende Figur
Eine Regel für reelle Zahlen gilt für Vektoren nicht, nämlich die Regel: a·b = 0 => a = 0 oder b = 0 (a, b eR).
Bei orthogonalen Vektoren ist das Skalarprodukt ja immer Null, auch wenn keiner der Nullvektor ist. Man kann jedoch festhalten.
→ → → → → → a · a > 0 und a ·a = 0 nur für a = 0
Der Mathematiker sagt dazu:
Das Skalarprodukt ist positiv definit.
Der Beweis dieser Beziehung sowie des KG und AG folgt direkt
aus den Definitionen, wobei man beim AG noch eine
Fallunterscheidung für positives und
negatives k machen muss. Man spricht vom gemischten
Assoziativgesetz, weil hier Skalar und Vektor gemischt
werden.
Zum DG betrachte man folgende Figur:
Der besseren Veranschaulichung wegen sind für die
Vektoren eine Kraft und zwei Strecken eingezeichnet und das
Skalarprodukt mit W = Arbeit bezeichnet.
Behauptung:
→ → → → → → → → →
F ·s = F ·(s + s ) = F·s + F·s
1 2 1 2
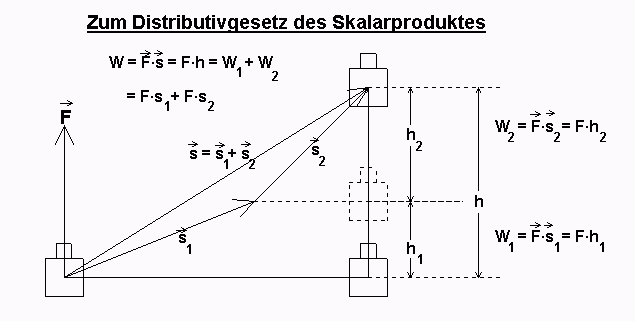
Beweis: Für die Physiker ist klar:
Die verrichtete Arbeit richtet sich nur nach dem Höhenunterschied h = h + h .
1 2
Die Mathematiker überzeugt man mit der ersten Figur, dort sieht man:
|F|·|s|·cos(α) = |F|·h, wobei h die Projektion von s senkrecht zu F ist.
Jetzt sind wir in der Lage, das Skalarprodukt von Vektoren
mit Hilfe ihrer Koordinaten zu berechnen:
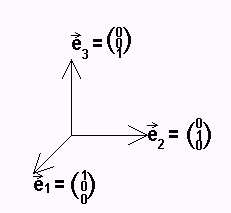
Für die Einheitsvektoren
|1| |0| |0|
→ | | → | | → | |
e = |0|, e = |1| und e = |0| gilt:
1 | | 2 | | 3 | |
|0| |0| |1|
→ → → → → →
e ·e = 1·1·cos(0°) = 1 und analog e ·e = 1 und e ·e = 1,
1 1 2 2 3 3
→ → → → → →
sowie e ·e = e ·e = e ·e = 0 wegen der Orthogonalität.
1 2 1 3 2 3
|a |
→ | 1| → → →
Sei a = |a | = a ·e + a ·e + a ·e und
| 2| 1 1 2 2 3 3
|a |
| 3|
|b |
→ | 1| → → →
b = |b | = b ·e + b ·e + b ·e .
| 2| 1 1 2 2 3 3
|b |
| 3|
Dann folgt (eine längere aber höchst einfache Rechnung)
→ → → → → → → →
a ·b = (a ·e + a ·e + a ·e )·(b ·e + b ·e + b ·e )
1 1 2 2 3 3 1 1 2 2 3 3
→ → → → → →
= a e ·b e + a e ·b e + a e ·b e
1 1 1 1 1 1 2 2 1 1 3 3
→ → → → → →
+ a e ·b e + a e ·b e + a e ·b e +
2 2 1 1 2 2 2 2 2 2 3 3
→ → → → → →
+ a e ·b e + a e ·b e + a e ·b e
3 3 1 1 3 3 2 2 3 3 3 3
= a b + 0 + 0
1 1
+ 0 + a b + 0
2 2
+ 0 + 0 + a b
3 3
= a b + a b + a b
1 1 2 2 3 3
|a | |b |
| 1| | 1|
Somit folgt: |a |·|b | = a b + a b + a b
| 2| | 2| 1 1 2 2 3 3
|a | |b |
| 3| | 3|
Merke!
(Der 2. Hauptsatz für das Skalarprodukt)→ → a ·b = |a|·|b|·cos(α) = a b + a b + a b 1 1 2 2 3 3
Insbesondere folgt: Der Winkel a zwischen zwei Vektoren → → a · b berechnet sich zu cos(α) = ———————, wobei |a|·|b| ——————————— → → / 2 2 2 a ·b = a b + a b + a b und |a| = \/ a + a + a ist. 1 1 2 2 3 3 1 2 3
Im zweidimensionalen gilt entsprechend: |a | —————— |a | |b | | 1| / 2 2 | 1| | 1| |a | = \/ a + a |a |·|b | = a b + a b | 2| 1 2 | 2| | 1| 1 1 2 2 Falls Du einmal mit vierdimensionalen Vektoren rechnen musst, wird Dir der Übergang nicht schwer fallen.
Trivial und dann doch wieder bemerkenswert ist folgender Sachverhalt:
Merke!
→ 2 2
a = a
————
|→ | → 2
a = |a | = \/ a
→ Mit der Bezeichnung a = |a | gilt: ——— 2 → 2 → 2 → /→ 2 a = |a | = a , also a = |a | = \/ a
Nachweis: |a | → | 1| → 2 → → Für a = |a | gilt a = a ·a = a a + a a + a a | 2| 1 1 2 2 3 3 |a | | 3| ———————————— → / 2 2 2 2 → 2 und a = |a | = \/ a + a + a also a = a . 1 2 3 → 2 2 Oder: Nach Definition: a = |a|·|a|cos(0°) = |a|·|a| = a·a = a .
Im Beweis der folgenden Sätze zeigt sich:
Das Skalarprodukt ermöglicht, komplizierte Sätze, bei denen von Winkel die Rede ist, einfach zu beweisen.
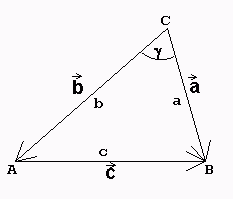
Kosinussatz
2 2 2
c = a + b - 2abcos(γ)
Beweis: Mit Hilfe der eingezeichneten Vektoren folgt:
→ → → →
c = a - b (Die Richtung von c nach rechts oder
links ist willkürlich.) =>
→ 2 → 2 → 2 → → 2 2 2
c = a + b - 2a b und damit c = a + b - 2ab cos(γ),
→ →
da nach Definition a ·b = abcos(γ). Für γ = 90° ist cos(γ)=0
2 2 2
und damit ergibt sich der Spezialfall c = a + b (Pythagoras!)
Beweis des Thalessatzes
Voraussetzung: r = r = r = r (die Länge der Vektoren ist gleich.
1 2 3
→ →
und r = - r .
2 1
→ → →2 2
Beachte: r ·r =-r = -r
1 2 1
Behauptung: a und b orthogonal.
→ →
Zu zeigen: a ·b = 0
→ → → → → →
Nachweis: a ·b = (r - r )·(r - r )
2 3 1 3
→ → → → → → → 2 2 → → → → 2
= r ·r - r ·r - r ·r + r = -r - r ·r - r ·r +r
2 1 2 3 3 1 3 2 3 3 1
→ → → →
= - r ·(r + r ) = -r ·0 = 0
3 2 1 3
Einen elementaren Beweis findest Du hier....
Das Vektorprodukt
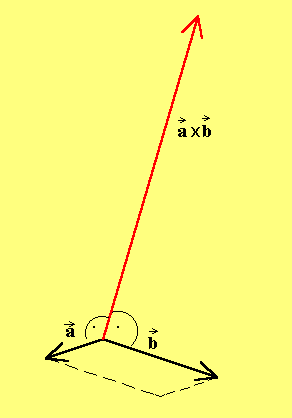
Mit Hilfe des Vektorproduktes kann man zu je zwei Vektoren einen Vektor bilden, der zu beiden Vektoren senkrecht ist.
Seine Länge entspricht dem Flächeninhaltes des gestrichelten Parallelogramms.
In der Physik wird es zum Beispiel benötigt, um die Kraft auf einen elektrisch bewegten Leiter im Magnetfeld auszurechnen. Hier ist der eine Vektor in Stärke und Richtung der Bewegung gegeben, der zweite in Betrag und Richtung des magnetischen Feldes. Das Vektorprodukt der beiden Vektoren gibt dann Betrag und Richtung der Kraft auf den elektrischen Leiter nach der "rechten-Hand-Regel" an.
Im Gegensatz zum Skalarprodukt, das in Vektorräumen beliebiger Dimension definiert werden kann, gibt es das Vektorprodukt nur im 3-dimensionalen Räumen. Dort allein ist das Vektorprodukt von zwei linear unabhängigen Vektoren bis auf den Betrag eindeutig als ein Vektor definiert, der auf beiden Faktoren senkrecht steht.
Die Einführung zum Vektorprodukt hier soll nur eine Rechenhilfe für manche Aufgaben bereitstellen. In Baden-Württemberg gehört es nicht zum Lehrplan der Oberstufe (Stand: 2017). Es zu beherrschen, ist sehr vorteilhaft. Und wenn man es schon benutzt- und sei es nur als Rechenhilfe -, ist es wiederum gewinnbringend, das Wesentliche über das Vektorprodukt zu erfahren.
Definition:
|a | |b | |a b - b a |
→ | 1| → | 1| → → | 2 3 2 3|
Für a = |a | und b = |b | ist a x b = |a b - b a |
| 2| | 2| | 3 1 3 1|
|a | |b | |a b - b a |
| 3| | 3| | 1 2 1 2|
Wegen der Schreibweise "x" wird des Vektorprodukt
manchmal auch Kreuzprodukt genannt.Im Gegensatz zum Skalarprodukt ist das Vektorprodukt von zwei Vektoren wirklich ein Vektor und keine reellle Zahl (Skalar).
Folgende "Eselsbrücke" hat sich als Merkregel bewährt:
- Schreibe beide Vektoren zwei Mal nebeneinander und untereinander auf.
- Streiche die erste und letzte Zeile.
- Bilde die Differenz der "über Kreuz" gebildeten Produkte.
1. Schritt 2.Schritt 3.Schritt
|a b |
| 1 1|
|a b | |a b |
| 2 2| | 2 X 2| |a b - b a |
|a b | |a b | | 2 3 2 3|
→ → | 3 3| | 3 3| |a b - b a |
a x b = | | = | X | = | 3 1 3 1|
|a b | |a b | |a b - b a |
| 1 1| | 1 X 1| | 1 2 1 2|
|a b | |a b |
| 2 2| | 2 2|
|a b |
| 3 2|
Beispiele (der erste Schritt wird übersprungen):
|2 1|
|3| |4| | X | |2·2 - 1·1| | 3|
| | | | |1 2| | | | |
a) |2|x|1| = | X | =|1·4 - 2·3| = |-2|
| | | | |3 4| | | | |
|1| |2| | X | |3·1 - 4·2| |-5|
|2 1|
Bemerkung: Das "X" ist hier ist eine behelfsmäßige Schreibweise für folgende Zeichnung:
Satz: Das Vektorprodukt zweier Vektoren ist ein Vektor, der senkrecht auf beiden Vektoren steht.| 2 -1| |-3| |-2| | X | |10 - 1| | 9| | | | | |-1 5| | | | b) | 2|x|-1| = | X | =|2 + 15| = |17| | | | | |-3 -2| | | | |-1| | 5| | X | |3 + 4| | 7| | 2 -1| (Wie immer auf Vorzeichen achten!) |-1 -4| |-3| |-5| | X | | -1 + 8| | 7| | | | | | 2 1| | | | | c) |-1|x|-4| =| X | = |-10 + 3| = |-7|. | | | | |-3 -5| | | | | | 2| | 1| | X | | 12 - 5| | 7| |-1 -4|
Der Beweis erfolgt einfach durch ausrechnen: Das Skalarprodukt muss Null ergeben:
|a | |a b - b a |
→ → → | 1| | 2 3 2 3|
a · a x b = |a |·|a b - b a |
| 2| | 3 1 3 1|
|a | |a b - b a |
| 3| | 1 2 1 2|
= a (a b - b a ) + a (a b - b a ) + a (a b - b a ) = 0
1 2 3 2 3 2 3 1 3 1 3 1 2 1 2
|b | |a b - b a |
→ → → | 1| | 2 3 2 3|
b · a x b = |b |·|a b - b a |
| 2| | 3 1 3 1|
|b | |a b - b a |
| 3| | 1 2 1 2|
= b (a b - b a ) + b (a b - b a ) + b (a b - b a ) = 0
1 2 3 2 3 2 3 1 3 1 3 1 2 1 2
In diesem Zusammenhang werden die folgenden Ausführungen nicht benötigt. Sie sind jedoch für das Verständnis des dreidimensionalen Vektorraumes wissenswert.
Regeln für das Vektorprodukt
das Distributivgesetz
→ → → → → → → a x(b + c ) = a x b + a x c
das gemischte Assoziativgesetz
→ → → → → → (ka ) x b = a x (kb ) = k(a x b ) für k e R
Das Antikommutativgesetz
→ → → → b x a = - a x b
Das Produkt der Einheitsvektoren
→ |1| → |0| → |0|
Für e = |0|, e = |1| und e = |0| gilt:
1 |0| 2 |0| 3 |1|
→ → → → → → → → →
e x e = e , e x e = e und e x e = e
1 2 3 2 3 1 3 1 2
Das Vektorquadrat
Umgekehrt gilt:
Ist das Vektorprodukt Null, dann sind die Faktoren linear abhängig.
→ → →
stets ist a x a = 0 . Allgemeiner:
Das Vektorprodukt von linear abhängigen Vektoren ist Null.
Umgekehrt gilt:
Ist das Vektorprodukt Null, dann sind die Faktoren linear abhängig.
Der Betrag des Vektorpruduktes ist
gleich der Fläche des von den beiden
Vektoren aufgespannten Parallelogramms.
gleich der Fläche des von den beiden
Vektoren aufgespannten Parallelogramms.
|→ → → → |a x b | = |a ||b |sina| a = Winkel, den die Vektoren einschließen
Das Assoziativgesetz hier heißt "gemischt", weil dabei Vektoren und Skalare gemischt werden.
Das ("ungemischte") Assoziativgesetz gilt nicht, was man am folgendem Beispiel erkennt:
→ → → → → → → →
(e x e ) x e ? e x (e x e ) , nämlich 0 ? - e
1 1 2 1 1 2 2
Dass das Kommutativgesetz nicht gilt, ist offensichtlich:
Beim Vertauschen der Faktoren ändert sich das Vorzeichen.Test auf Basiswissen
1. Schreibe einen beliebigen Vektor (zwei- oder dreidimensional auf) und berechne seinen Betrag. Kontrolliere das Ergebnis mit TTMathe! Zum Beispiel:
|4| |6 | |4,8| |1| |-2|
a) | | , | |, | |, | |, | |
|3| |2,5| |1,4| |2| |6 |
|-1| | 2| |-2| |-3| | 1|
| | | | | | | | | |
b) | 2|, |-3|, |-6|, |-4| , |-2|
| | | | | | | | | |
|-2| | 6| | 9| |12| | 3|
2. Schreibe zwei beliebige Vektoren auf und berechne den
Winkel, den die Vektoren einschließen. Kontrolliere das
Ergebnis mit TTMathe! Zum Beispiel:
| 2| |3|
→ |4| → |12| → | | → | |
a) a = | | b = | | b) a = |-4| b = |2|
|3| |-5| | | | |
| 1| |5|
3. Schreibe drei beliebige Punkte eines Dreiecks hin und
berechne die Innenwinkel. Kontrolliere das Ergebnis mit
TTMathe!Zum Beispiel:
A(1|-2|1)B(-3|1|4)C(5|-2|1)Lösungen: siehe 33. Lektion
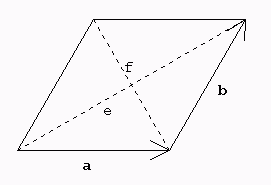
Raute
4. a) Beweise, dass in einer Raute die Diagonalen othogonal zueinander sind! Das heißt:Ist a = b, dann stehen e und f senkrecht aufeinander.
→ → Hinweis: Führe Vektoren a und b ein und stelle die → → Diagonalen als Linearkombinationen von a und b dar. b) Beweise auch die Umkehrung!
Lösungen
Anwendungen
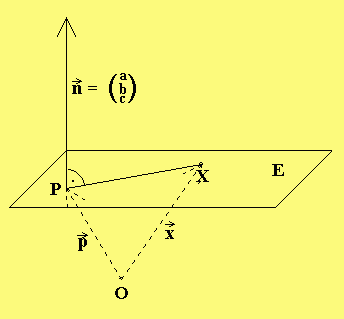
E: ax + bx + cx = d
1 2 3
Die Normalenform der Ebenengleichung
→ →
Sei n ein Normalenvektor von E, d.h. n
verläuft senkrecht zu E und sei P ein fester
Punkt von E. Dann gilt für alle Punkte X e E:
——> →
PX senkrecht n , d.h.
→ → →
(x - p )·n = 0, wobei
→ →
x und p die Ortsvektoren von X und P sind.
→ | 2|
Sei zum Beispiel n = |-2| und P(3|-2|5), dann
| 1|
gilt für alle Punkte X(x |x |x ) e E:
1 2 3
|x - 3| | 2|
| 1 | | |
|x + 2|·|-2| = 0,
| 2 | | |
|x - 5| | 1|
| 3 | | |
also E: 2x -2x + x - 15 = 0.
1 2 3
Wir haben also gezeigt:
→ |a| |
Ist n = |b| ——— E, dann lautet die Gleichung der Ebene:
|c|
|x - p | |a|
| 1 1| | |
E: |x - p |·|b| = 0
| 2 2| | |
|x - p | |c|
| 3 3| | |
oder a(x - p ) + b(x - p ) + c (x - p ) = 0
1 1 2 2 3 3
oder E: ax + bx +cx = d für ein passendes d e R.
1 2 3
Umgekehrt gilt:
Sind nämlich P(p |p |p ) und Q(q |q |q ) zwei beliebige Punkte von E,
1 2 3 1 2 3
also Punkte, deren Koordinaten die Gleichung
ap + bp +cp = d und aq + bq + cq = d erfüllen, dann
1 2 3 1 2 3
|a| |q - p | |a|
——> | | | 1 1| | |
gilt PQ · |b| = |q - p |·|b| = (q - p )a + (q - p )·b + (q - p)·c
| | | 2 2| | | 1 1 2 2 3 3
|c| |q - p | |c|
| | | 3 3| | |
= (aq + bq + cq ) - (ap + bp +cp ) = d - d = 0.
1 2 3 1 2 3
→ |a| | ——> ——>
Somit ist n = |b| ——— PQ für alle möglichen Richtungen PQ von E,
|c|
→ |
d.h. n ——— E.
Die Hesse-Form...
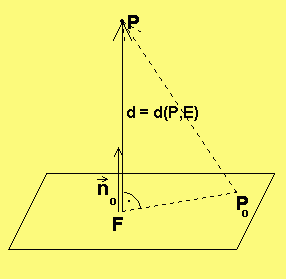
... dient zur A b s t a n d s berechnung.
→ → →
Gegeben ist die Ebene E durch E: (x - p )·n = 0
o
und ein Punkt P(p |p |p ).
1 2 3
→
Ersetzten wir nun den Normalenvektor n der Ebene E
→
→ n
durch einen Einheitsvektor n = ————, so erhalten
o |→ |
|n |
→ → →
wir die Hessesche Normalenform E: (x - p )·n = 0
o 0
und der Abstand d = d(P,E) berechnet sich zu
|a|
| → → → | → 1 | |
d = |(p - p )·n | mit n = ————————————·|b|
| 0 0| 0 ————————— | |
/2 2 2 |c|
\/a + b + c
Beweis: F sei die senkrechte Projektion von P auf E, d.h. der Schnittpunkt der Geraden
senkrecht zu E durch P mit E. Der Trick bei der Hesseform ist, dass F für die Berechnung
nicht benötigt wird: F fällt heraus.) Der Abstand d des Punktes P von E soll berechnet werden.
→ → ——>
Der Einheitsvektor n hat die Länge 1 und es ist deshalb d·n = FP .
0 0
→
(n könnte auch die entgegengesetzte Richtung haben.
0
Da wir aber letztendlich mit dem Betrag rechnen,
können wir diesen Fall vernachlässigen.)
Jetzt kommt der Trick:
→ → ——> → → → ———> →
Aus n ·n = 1 folgt FP ·n = dn ·n = d und, da P F ·n = 0
0 0 0 0 0 0 0
→ → → ———> → ———> ——> →
ergibt sich (p - p )·n = P P ·n = (P F + FP )·n
0 0 0 0 0 0
——> →
= 0 + FP· n = d.
0
Den vorhin erwähnten zweiten Fall berücksichtigend ist also
| → → → |
d = |(p - p )·n |.
| 0 0|
Die Hesseform als Kordinatengleichung
Die Hesseform von E: ax + bx + cx = e lautet
1 2 3
ax + bx +cx -e
1 2 3
E: ———————————————— = 0
—————————
/2 2 2
\/a + b + c
|ap + bp + cp -e|
| 1 2 3 |
und der Abstand P(p |p |p ) von E ist dann d = |————————————————|
1 2 3 | ————————— |
| /2 2 2 |
| \/a + b + c |
Der Zusammenhang der Vektordarstellung mit der
Koordinatenform ist nämlich folgender:
|x - p | |a|
→ → → | 1 01| | |
(x - p )·n = 0 äquivalent |x - p |·|b| = 0
0 | 2 02| | |
|x - p | |c|
| 3 03| | |
äquivalent a(x - p ) + b(x - p ) + c(x - p ) = 0
1 01 2 02 3 03
äquivalent ax + bx + cx - e = 0
1 2 3
für e = ap + bp + cp und P (p |p |p ).
01 02 03 0 01 02 03
Beispiel: Der Abstand des Punktes P(-7|11|-13)
von der Ebene E: 2x - 3x + 6x = 24
1 2 3
berechnet sich über die Hesse-Form der Ebenengleichung
2x - 3x + 6x - 24
1 2 3
E: —————————————————— = 0
—————————
/2 2 2
\/2 + 3 + 6
|2·(-7) - 3·11 + 6·(-13) - 24| 2
zu d = d(P,E) = |————————————————————————————| = 21-.
| 7 | 7
Du kannst diese Rechnung und Deine Rechnungen überprüfen mit
TTmathe|Geometrie Punkt Abstand.
Abstand Punkt-Geraden
Hinweis. Siehe auchAufgabe 8b mit Lösung.Windschief
Der Abstand windschiefer Geraden
Dieser Abschnitt ist für Fortgeschrittene!
Rechnung wird ausgeführt:
TTMathe|Geometrie|Zwei
Geraden
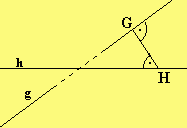
Gegeben seien zum Beispiel die windschiefen Geraden
| 9| |-2| | 1| |0|
→ | | | | → | | | |
g: x = |10| + s·| 1| und h: x = |-3| + t·|1|
| | | | | | | |
|-2| | 0| |-4| |3|
Um den Abstand der beiden Geraden zu bestimmen wählen
wir einen Punkt G(9-2s|10+s|-2) auf g und einen Punkt
H(1|-3+t|-4+3t) auf h und bestimmen s und t so, dass
——>
der Vektor GH senkrecht zu g und senkrecht zu h verläuft.
Senkrecht stehen heißt: Skalarprodukt der Richtungsvektoren = 0.
|-2| |0| | -8+2s |
——> | | ——> | | ——> | |
=> GH · | 1| = 0 und GH · |1| = 0 mit GH = |-13+t-s|. Also
| | | | | |
| 0| |3| | -2+3t |
-2(-8+2s) + 1(- 13+t-s) + 0 = 0 oder -5s + t = -3 (1)
und 0 + 1(-13+t-s) + 3(-2+3t) = 0 oder -s + 10t = 19 (2)
Das LGS (1) und (2) hat die Lösung s = 1 und t = 2.
Einsetzen des Parameter s = 1 ergibt G(7|11|-2) und t = 2
ergibt H(1|-1|2). Der Abstand der windschiefen Geraden ist also
——————————————————————————
/ 2 2 2
d(g,h) = d(G,H) = \/(1-7) + (-1-11) + (2 + 2) = 14 LE
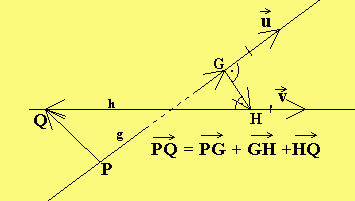
Alternative Rechnung
Einfacher, aber theoretisch anspruchsvoller:
(Wer die Herleitung überspringen will, gehe
→ → →
gleich zur Formel d(g,h) = |(q - p )·n | weiter unten.)
0
→
Sei u der Richtungsvektor von g und
→
v der Richtungsvektor von h.
|-2| |0|
→ | | → | |
Im Beispiel hier also u = | 1| und v = |1|.
| | | |
| 0| |3|
Dann suchen wir zunächst
|a|
→ | | → → → →
einmal einen Vektor n = |b| mit n · u = 0 und n · v = 0.
| |
|c|
Mit Hilfe des Vektorproduktes kann man
|-2| |0| |3 - 0| | 3|
→ | | | | | | | |
diesen direkt berechnen: n = | 1|x|1| = |0 + 6| = | 6|.
| | | | | | | |
| 0| |3| |-2 - 0| |-2|
Ohne Kenntnis des Vektorproduktes können wir folgendermaßen vorgehen:
Wir lösen das LGS -2a + b = 0 und b + 3c =0. Wählen wir etwa a = 3 (beliebig),
dann muss b = 6 und c = - 2 sein. Eine Lösung des LGS ist also
| 3|
→ | |
n = | 6|. (Die Lösung ist bis auf ein Vielfaches eindeutig!)
| |
|-2|
Als nächsten bestimmen wir einen Einheitsvektor n
0
→ → 1 →
(bis auf das Vorzeicheneindeutig!) von n , hier also n = - n .
0 7
Jetzt kommt der geniale Trick:
——>
GH ist ein Vielfaches von n .
0
→ →
Beide Vektoren stehen ja senkrecht auf u und auf v .
——>
Noch mehr: Aus GH = x·n (was ja für ein x möglich ist) folgt:
0
——>
|GH | = |x|·|n | = |x|·1 = |x|.
0
——>
d.h. x gibt bis auf das Vorzeichen die Länge von GH und damit
den Abstand d(g,h) an!
——> → → → → →
Es kommt noch toller: GH ·n = x·n ·n = x, da n ·n = 1.
0 0 0 0 0
Und: Wähle ich einen beliebigen Punkt P auf g
und einen beliebigen Punkt Q
——> → ——> ——> ——> ——>
auf h, dann ist PQ ·n = (PG + GH + HQ)·n = GH ·n = x,
0 0 0
——> ——> ——> ——>
da ja PG und HQ auf n senkrecht stehen, also PG·n = HQ·n = 0 ist.
0 0 0
Somit erhalten wir als Formel für den Abstand zweier windschiefer Geraden:
→ → →
d(g,h) = |(q - p )·n |, wobei p und q Ortsvektoren beliebiger Punkte
0
→
von g und h und n ein Einheitsvektor senkrecht zu g und h ist.
0
| 9| | 1| | 3|
→ | | → | | → 1| |
Im Beispiel wählen wir p = |10|, q = |-3| und n = -| 6|.
| | | | 7| |
|-2| |-4| |-2|
1
Der Abstand berechnet sich dann zu d(g,h) = -|(-8)·3+(-13)·6+(-2)·(-2)| = 14 LE
7
Test auf Basiswissen
5. Bestimme die Gleichung der Ebene durch P(3|-7|11)
| 2|
mit dem Normalenvektor n = |-5|!
| 0|
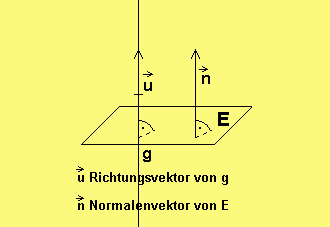
6. Gegeben Ebene E und Punkt P (beliebig).
Gesucht Gerade g senkrecht zu E durch P.
Beispiel E: 2x - 7x = 25, P(0|8|-11)
1 3
7. Umgekehrt: Gegeben Gerade g und Punkt P.
Gesucht Ebene E senkrecht zu g durch P.
→ |-3| | 0|
Beispiel: g: x = | 1| + t·|-1|, P(1|2|-3)
|-5| | 2|
8. Abstandsberechnungen. Kontolliere Deine Ergebnisse mit TTMathe! a) Schreibe eine beliebige Ebene E und einen Punkt P auf und berechne den Abstand d(P,E)! Zum Beispiel: E: 2x -x - 5x = 3 P(-1|2|1) 1 2 3 Berechne den Abstand auch ohne die Hessesche Normalenform von E! b) Schreibe eine beliebige Gerade g und einen Punkt P auf und berechne den Abstand d(P,g)! → |4| |1| Zum Beispiel g: x = |2| + t·|1| P(4|6|2) |1| |0| c) Schreibe zwei beliebige nichtparallele (und im Normalfall auch sich nicht schneidende also windschiefe) Geraden g und h auf und berechne ihren Abstand. |8| |3| | 7| |3| → | | | | → | | | | Zum Beispiel g: x = |8| + s·|2| und h: x = | 2| + t·|3| | | | | | | | | |5| |2| |10| |4|Lösungen