TTMathe Beispiele

TTMathe als intelligenter Rechner

2*8,5+4*(27.3-3/2) = 120,2 = 601/5 = 120'1/5 (Bemerkung:120'1/5=120+1/5 gemischte Zahl)
1'1/2+4'5/22  = 5,727 272 727 272 727 27 = 63/11 = 5'8/11
sqrt(32/225)*sqrt(21) = 1,728 197 519 575 429 4 = 4/15*sqrt(42)
sin(45°) = 0,707 106 781 186 547 524 = 1/2*sqrt(2)
tan(Pi/12)  = 0,267 949 192 431 122 706 = 2-sqrt(3)
PrZ(2^16) = 821 641 ("Die n-te Primzahl")
nue(6) = 13 983 816 ("n über x"; n=49 im Parameterfeld eingeben!)

TTMathe zeichnet Schaubilder

Gut geeignet, um Lehrinhalte zu veranschaulichen. Siehe Umkehrfunktionen.

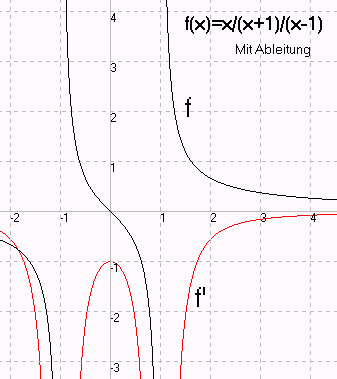
Beispiel 1: Schaubild einer Funktion mit Schaubild
der Ableitung.
(Original zeigt Bereich: -8 ≤ x ≤ 8; -6 ≤ y ≤ 6)

   Skript ("Funktion" und "Text")
x/(x+1)/(x-1)
Text 1,5 4 18 |f(x)=x/(x+1)/(x-1)
Text 2,5 3,4 10 |Mit Ableitung
Text 1,5 2,4 20 |f
Text 1,7 -1,4 20 |f'
—————————————————————————————Bemerkung:
         x-,  y-Wert
                  Schriftgröße des Textes

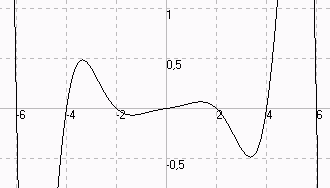
Beispiel 2: Bereich kann verändert werden.
(Original: -16 ≤ x ≤ 16; -3 ≤ y ≤ 3)

Hier: f(x) = 1/50*exp(abs(x))*sin(Pi/2*x)
      LEx = 1/2 ("Längeneinheit der x-Achse")
      LEy = 2   ("Längeneinheit der y-Achse")
(Vom Schaubild kann auch ein Auschnitt weiter
rechts/links oder oben/unten gezeigt werden.)

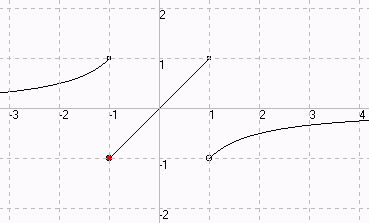
Beispiel 3: Schaubild einer abschnittsweis
definierten Funktion.
(Original: -8 ≤ x ≤ 8; -6 ≤ y ≤ 6)

    Skript ("Funktion + Leerstelle
            + Zeichenbereich"
            "Kästchen" bzw. "Kreis")
-1/x [-6,5;-1]
x [-1;1]
-1/x [1;5,5]
Kästchen -1 1 1/20
Kreis -1 -1 1/20
Kästchen 1 1 1/20 rot
Kreis 1 -1 1/20
———— Hinweis ——————————
Kreis 1 - 1 1/20 heißt:
Mittelpunkt M(1|-1)
r = 1/20 (Farbe weiß)

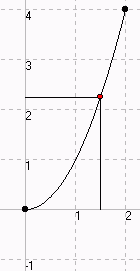
Beispiel 4: Strecken einzeichnen.

    Skript
x^2 [0;2]
Strecke 1,5 0 1,5 1,5^2
Strecke 0 1,5^2 1,5 1,5^2
Kreis 0 0 1/20 schwarz
Kreis 2 4 1/20 schwarz
Kreis 1,5 1,5^2 1/20 rot
———————— Hinweis ————————
Strecke 1,5 0 1,5 1,5^2
    bedeutet
Strecke von P(1,5|0) bis
Q(1,5|1,5^2)

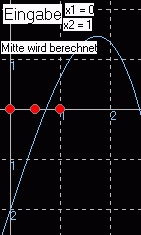
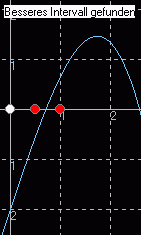
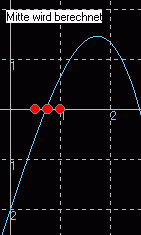
Intervallhalbierungsverfahren

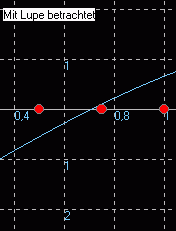
Im Programm zum Intervallhalbierungsverfahren (Downloadseite) wird folgendermaßen die Berechnung der Nullstelle durchgeführt und veranschaulicht. Programm in Delphi siehe Lektion 11.

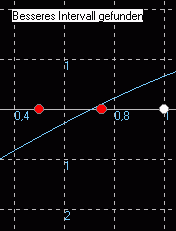
			Eingabe der Startwerte x = 0 1 x = 1 2 Mitte x = 0,5 3 Mitte von 0,5 und 1 x = 0,75 4
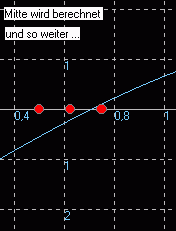
			Mitte von 0,5 und 0,75 x = 0,625 5

Die zugehörige Rechnung sieht dann folgendermaßen aus:

Gesucht: Nullstelle der Funktion
f(x) = -1/3*x^3+3*x-2 Im Intervall (0,1)
Rechnung:
      x                 f(x)
———————————————————————————————————————————
  x1 =          0      -  2
  x2 =          1         0,666 666 666 667
  x3 =        0,5      -  0,541 666 666 667
  x4 =       0,75               0,109 375
  x5 =      0,625      -  0,206 380 208 333
  x6 =     0,687 5     -  0,045 817 057 292
  x7 =    0,718 75        0,032 480 875 651
  x8 =   0,703 125     -  0,006 496 429 443
  x9 =  0,710 937 5       0,013 035 615 285
  ...  0,707 031 25       0,003 280 381 362
      0,705 078 125    -  0,001 605 334 381
     0,706 054 687 5      0,000 838 196 836
    0,705 566 406 25   -  0,000 383 400 552
   0,705 810 546 875      0,000 227 440 212
   0,705 688 476 563   -  0,000 077 969 655
   0,705 749 511 719      0,000 074 737 908
   0,705 718 994 141   -  0,000 001 615 215
   0,705 734 252 93       0,000 036 561 511
   0,705 726 623 535      0,000 017 473 189
   0,705 722 808 838      0,000 007 928 996
   0,705 720 901 49       0,000 003 156 893
   0,705 719 947 816      0,000 000 770 84
   0,705 719 470 978   -  0,000 000 422 187
   0,705 719 709 397      0,000 000 174 327
   0,705 719 590 187   -  0,000 000 123 931
   0,705 719 649 792      0,000 000 025 197
   0,705 719 619 989   -  0,000 000 049 367
   0,705 719 634 89    -  0,000 000 012 086
   0,705 719 642 341      0,000 000 006 555
   0,705 719 638 616   -  0,000 000 002 766
   0,705 719 640 478      0,000 000 001 895
   0,705 719 639 547   -  0,000 000 000 435
   0,705 719 640 012      0,000 000 000 729
   0,705 719 639 78       0,000 000 000 146
   0,705 719 639 663   -  0,000 000 000 144
   0,705 719 639 721      0,000 000 000 001
   Mit x37 =  0,705 719 639 721 wird die Rechengenauigkeit erreicht

Sekantenverfahren und Regula Falsi

Diese Verfahren (Downloadseite) dienen zur numerischen Nullstellenbestimmung. Die Nullstelle wird Schritt für Schritt immer besser angenähert.
Die Verfahren werden ähnlich wie beim Intervallhalbierungsverfahren veranschaulicht.

                    Sekantenverfahren
Vorgabe: x0,x1 so, dass f(x0)*f(x1) < 0
Sekante durch P0(x0|f(x0)) und P0(x1|f(x1)) hat Nullstelle in x2
Sekante durch P1(x1|f(x1)) und P2(x2|f(x2)) hat Nullstelle in x3
Sekante durch P2(x2|f(x2)) und P3(x3|f(x3)) hat Nullstelle in x4
Sekante durch P3(x3|f(x3)) und P4(x4|f(x4)) hat Nullstelle in x5
Sekante durch P4(x4|f(x4)) und P5(x5|f(x5)) hat Nullstelle in x6
...
so lange, bis |f(x_n)| klein genug!
Beispiel:
f(x)= -1/3*x^3+3*x-2
                x0=0        f(x0) = -  2
                x1=1        f(x1) = 2/3
Sekante durch (x0=0|-2)  und (x1=1|0,666667)                      hat Nullstelle
             x2=0,75     mit f(x2) = 0,109 375
Sekante durch (x1=1|0,666667)  und (x2=0,75|0,109375)             hat Nullstelle
   x3=0,700 934 579 439  mit f(x3) = -  0,011 988 150 62
Sekante durch (x2=0,75|0,109375)  und (x3=0,700935|-0,011988)     hat Nullstelle
   x4=0,705 781 220 688  mit f(x4) = 0,000 154 070 428
Sekante durch (x3=0,700935|-0,011988)  und (x4=0,705781|0,000154) hat Nullstelle
   x5=0,705 719 722 542  mit f(x5) = 0,000 000 207 214
Sekante durch (x4=0,705781|0,000154)  und (x5=0,70572|0,000000)   hat Nullstelle
    x6=0,705 719 639 72  mit f(x6)= -  0,000 000 000 004
    Rechengenauigkeit erreicht.
                      Regula falsi
Vorgabe: x0,x1 so, dass f(x0)*f(x1) < 0
Sekante durch P0(x0|f(x0)) und P0(x1|f(x1)) hat Nullstelle in x2
Sekante durch P0(x0|f(x0)) und P2(x2|f(x2)) hat Nullstelle in x3
Sekante durch P0(x0|f(x0)) und P3(x3|f(x3)) hat Nullstelle in x4
Sekante durch P0(x0|f(x0)) und P4(x4|f(x4)) hat Nullstelle in x5
Sekante durch P0(x0|f(x0)) und P5(x5|f(x5)) hat Nullstelle in x6
...
so lange, bis |f(x_n)| klein genug!
Hier wird vorausgesetzt, dass f zwischen x0 und x1 konvex oder konkav ist, d.h.
stets ist f(x0)*f(x_n) < 0. (Sonst könnte man das Verfahren verbessern, in dem man
P0(x0|f(x0)) aktualisiert. Auf jeden Fall muss der Vorzeichnwechsel garantiert sein.)
Beispiel:
f(x)= -1/3*x^3+3*x-2
                x0=0        f(x0) = -  2
                x1=1        f(x1) = 2/3
Sekante durch (0|-2)  und (1|0,666667) hat Nullstelle
             x2=0,75       mit f(x2) = 0,109 375
Sekante durch (x0=0|-2)  und (x2=0,75|0,109375) hat Nullstelle
   x3=0,711 111 111 111    mit f(x3) = 0,013 468 678 555
Sekante durch (x0=0|-2)  und (x3=0,711111|0,013469) hat Nullstelle
   x4=0,706 354 281 728    mit f(x4) = 0,001 587 564 454
Sekante durch (0|-2)  und (x4=0,706354|0,001588) hat Nullstelle
   x5=0,705 794 034 967    mit f(x5) = 0,000 186 130 008
Sekante durch (0|-2)  und (x5=0,705794|0,000186) hat Nullstelle
   x6=0,705 728 356 355    mit f(x6) = 0,000 021 808 613
Sekante durch (0|-2)  und (x6=0,705728|0,000022) hat Nullstelle
   x7=0,705 720 660 96     mit f(x7) =  0,000 002 555 099
Sekante durch (0|-2)  und (x7=0,705721|0,000003) hat Nullstelle
   x8=0,705 719 759 368    mit f(x8) = 0,000 000 299 353
Sekante durch (0|-2)  und (x8=0,70572|0,000000) hat Nullstelle
   x9=0,705 719 653 739    mit f(x9) = 0,000 000 035 072
Sekante durch (0|-2)  und (x9=0,70572|0) hat Nullstelle
   x10=0,705 719 641 363   mit f(x10) = 0,000 000 004 109
Sekante durch (0|-2)  und (x10=0,70572|0) hat Nullstelle
   x11=0,705 719 639 913   mit f(x11) = 0,000 000 000 481
Sekante durch (0|-2)  und (x11=0,70572|0) hat Nullstelle
   x12=0,705 719 639 744   mit f(x12) = 0,000 000 000 056
Sekante durch (0|-2)  und (x12=0,70572|0) hat Nullstelle
   x13= 0,705 719 639 724  mit f(13) = 0,000 000 000 007
   Rechnegenauigkeit erreicht.

Newtonverfahren

Dieses Verfahren (Downloadseite) dient zur numerischen Nullstellenbestimmung. Die Nullstelle wird Schritt für Schritt immer besser angenähert.
Programm in Delphi siehe Lektion 11. Es wird ähnlich wie beim Intervallhalbierungsverfahren veranschaulicht.

Beispiel:
Gesucht: Nullstelle der Funktion
f(x) = -1/3*x^3+3*x-2
Startwert: x0 = 0
Rechnung:
     x                     f(x)                   f'(x)
—————————————————————————————————————————————————————————————————
   x0 =   0                -  2                   3
   x1 = 0,666 666 666 667  -  0,098 765 432 099   2,555 555 556
   x2 = 0,705 314 009 662  -  0,001 014 986 191   2,502 532 148
   x3 = 0,705 719 593 339  -  0,000 000 116 045   2,501 959 856
   x4 = 0,705 719 639 721                  0      2,501 959 79
   Rechengenauigkeit mit x4 erreicht.

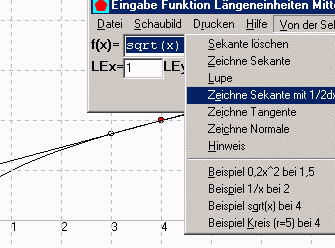
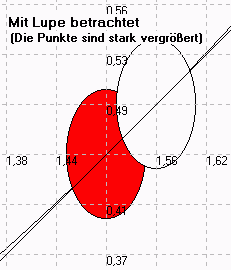
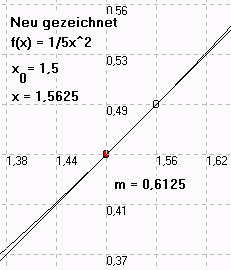
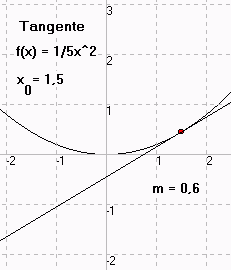
TTAbleitung: Von der Sekante zur Tangente

Mit dem Programm TTAbleitung ...

...können Sie für beliebige Funktionen zeigen, wie die Sekante sich allmählich einem Grenzwert nähert. Dabei können Sie die zugehörigen x-Werte automatisch immer mehr annähern lassen und das Ganze mit einer immer stärkeren "Lupe" betrachten. Das Programm berechnet dabei die Steigung und die Gleichung der Sekante sowie der Tangente und Normalen.

Downloadseite
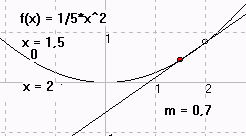
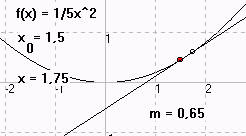
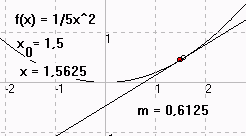