Joachim Mohr Mathematik Musik

Flächenberechnungen
Das (Riemann-)Integral

Bei dieser Betrachtung liegt der Schwerpunkt nicht bei der Herleitung einer Formel, sondern es soll hier exemplarisch gezeigt werden,
wie genial Mathematiker Probleme lösen.

Durch Verallgemeinerung des Problems Strukturen des Lösungsumfeldes aufdecken.

Das eigentliche Problem ist dann nur noch eine einfache Anwendung der entwickelten Theorie.

Und ist es im Alltagsleben - beruflich oder privat - nicht oft genauso? Und deshalb ist eine mathematische Bildung - neben dem Erlernen des logischen Denkens und der Ausbildung eines räumlichen Vorstellungsvermögens - so wertvoll.

Problem: Wie kann ich für möglichst viele Funktion f den Flächeninhalt A des "krummlinigen" Trapezes unter dem Schaubild von f über dem Intervall [a,b] berechnen?

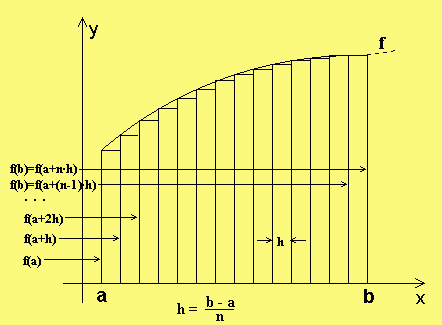
Gesucht ist also der Flächeninhalt zwischen dem Schaubild von f, der x-Achse und den Geraden mit den Gleichungen x=a und x=b (a < b).

Mit der Berechnung des Flächeninhaltes löst man viele weitere Probleme. Zum Beispiel:

Bestimmung des zurückgelegten Weges, wenn die Geschwindigkeit in Abhängigkeit von der Zeit gegeben ist.
Bestimmung der aufgewendeten Arbeit, wenn die Kraft entlang des Weges in Abhängigkeit des Weges gegeben ist.
Bestimmung der aufgewendeten Arbeit, wenn die Leistung in Abhängigkeit von der Zeit gegeben ist.
Bestimmung des transportierten Öls, wenn die Durchflussgeschwindigkeit in einer Pipeline in Abhängigkeit von der Zeit gegeben ist.

Beim ersten Lesen kannst Du von der Annahme ausgehen, dass f(x) ≥0 für alle xε[a,b] und a < b ist. Alle Überlegungen sind jedoch auch gültig, wenn f negative Werte annimmt oder b < a ist. In diesem Fall wird die "orientierte" Fläche betrachtet. Zum Beispiel werden Flächen unterhalb der x-Achse negativ gewertet. Physikalisch gesprochen: Ein Pendel, das nach oben schwingt, erhöht seine Lageenergie, die zugeführte Arbeit (siehe oben) wird positiv gewertet. Schwingt das Pendel nach unten, wird die abgegebene Energie negativ gewertet.

Für viele Jahrhunderte die einzige Lösungsmöglichkeit:

Unterteile die Fläche in n "krummlinige" Trapeze und berechne den Flächeninhalt der darunterliegenden Rechtecke:

Hier (bei einer monoton steigenden Funktion) berechnet sich die "Untersumme" zu
A_U = [f(a) + f(a+h) + f(a+2h) + ... + f(a+(n-1)h]·h
Entsprechend berechnet sich die "Obersumme" zu
A_O = [f(a+h) + f(a+h) + f(a+2h) + ... + f(a+h)]·h.
Es gilt: A_U < A < A_O. Als Näherungswert kann man etwa den Mittelwert der Untersumme und Obersumme für "großes" n wählen. Nur bei ganz wenigen Kurven konnte man durch Übergang zum Grenzwert für n → ∞ den exakten Wert bestimmen. (Archimedes mit seiner ähnlich durchgeführten "Exhaustionsmethode" gerade noch bei den Parabeln).

Für theoretische Untersuchungen sind die Untersummen und Obersummen noch von entscheidender Wichtigkeit. Der Mathematiker sagt: Die Fläche "existiert", wenn der Grenzwert der Untersummen gleich dem Grenzwert der Obersummen ist (siehe unten Riemannsches Integral). Man kann beweisen, dass dies zum Beispiel für alle "stückweise stetige" oder auch für alle monotonen Funktionen erfüllt ist. Funktionen, die hier Schwierigkeiten machen, lernt man an der Schule nicht kennen.

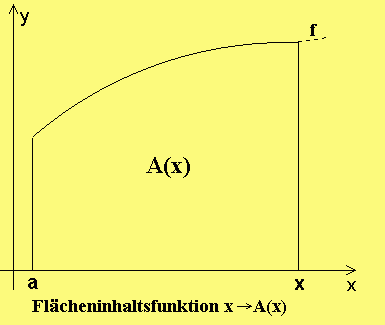
Das abstraktere und schwieriger aussehende Problem:

Wie kann ich für alle xεD_f den Flächeninhalt A(x) des "krummlinigen" Trapezes unter dem Schaubild von f über dem Intervall [a,x] berechnen?

Wenn es schon für ein spezielles x=b schwierig genug ist, wie soll ich es dann gleich für alle x berechnen können?

Der Mathematiker denkt anders. Er fragt sich:

Was kann ich über die Funktion x→A(x) aussagen?

Jetzt kommt die Überraschung:

x→A(x) ist eine Stammfunktion von x→f(x).

Nach Definition ist A Stammfunktion von f, wenn A'=f ist.

Da sich Stammfunktionen von f nur durch eine Konstante unterscheiden, gilt für eine beliebige Stammfunktion F die Beziehung A(x) = F(x) + C. Mit A(a)=0 und 0 = F(a) + C ergibt sich A(x) = F(x) - F(a). Somit:

A = A(b) = F(b) - F(a)

Und unser Problem, den Flächeninhalt eines krummlinigen Trapezes zu bestimmen (oder den zurückgelegten Weg oder die durch eine Pipeline geflossen Ölmenge und so weiter) ist für alle Funktionen, bei denen wir eine Stammfunktion angeben können, gelöst.

Einfach genial!

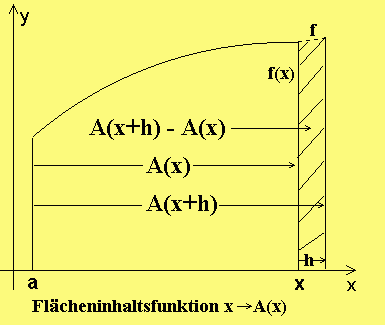
Dass A Stammfunktion von f ist, ist leicht plausibel zu machen:

Du musst dich nur an die Definition der Ableitung erinnern:

                   f(x+h)-f(x)
Def.: f'(x) = lim  ——————————— (Unten wird dies auf A angewendet!)
              h→0     h

Behauptung: A ist Stammfunktion von f, d.h. A'(x) =f(x)

Beweisidee:

Für das schraffierte "Rechteck" gilt:
A(x+h) - A(x) = f(x)·h.

Das Gleichheitszeichen gilt eigentlich erst, wenn wir den Übergang h → 0 machen. Die Mathematiker arbeiten hier deshalb mit Ungleichungen. Um die Idee plausibel zu machen, genügt zu wissen: Je kleiner h ist, um so kleiner ist der Fehler.

                          A(x+h)-A(x)        f(x)·h
Somit folgt: A'(x) = lim  ——————————— = lim  —————— = f(x)
                     h→0      h         h→0    h

∎