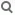Joachim Mohr Mathematik Musik Delphi
Der axiomatische Aufbau der affinen Ebenen, Translationsebenen, Desuargueschen Ebenen, präeuklidische Ebenen und euklidischen Ebenen.
nach Olaf Tamaschke, Universität Tübingen, SS 1964,
Heinz Lüneburg: Die euklidische Ebene und ihre Verwandten. Birkhäuser Verlag. Basel 1999
Hermann Hähl: Synthetische Geometrie, Vorlesung an der Universität Stuttgart, SS 2003
Heinz Lüneburg: Die euklidische Ebene und ihre Verwandten. Birkhäuser Verlag. Basel 1999
Hermann Hähl: Synthetische Geometrie, Vorlesung an der Universität Stuttgart, SS 2003
Affine Ebenen
Definition: Ein linearer Raum ist ein Paar (X,G), wobei X eine Menge (die Menge der "Punkte") und G (die Menge der "Geraden") eine Teilmenge der Potenzmenge 2X ist mit folgender Eigenschaft:(V) ("Verbindung") Zu je zwei Punkten x, y ε X existiert genau eine Gerade g ε G mit x ε g und y ε g.
Diese eindeutig bestimmte Gerade wird mit (x,y) bezeichnet.
Drei Punkte (oder allgemeiner: eine Menge von Punkten) heißen kollinear, wenn sie alle auf einer Geraden liegen.
Zwei verschiedene Geraden haben demnach höchstens einen gemeinsamen Punkt, genannt Schnittpunkt.
Definition: Zwei Geraden heißen parallel, wenn sie keinen Schnittpunkt haben und jede Gerade ist parallel zu sich selbst.
Definition: Ein linearer Raum heißt affine Ebene, wenn außer (V) noch folgende zwei Axiome gelten:
(P) ("Euklidisches Parallelenaxiom): Zu jeder Geraden g und zu jedem Punkt p existiert genau eine zu g parallele Gerade, die p enthält.
(R3) (Reichhaltigkeit): Es gibt drei nicht-kollineare Punkte.
Die folgenden Sätze beziehen sich alle auf die affine Ebene.
 Direkte Folgerungen von (R3) sind:
Direkte Folgerungen von (R3) sind:
Lemma: Es gibt mindestens 3 Geraden, die sich nicht in einem Punkt treffen.
Beweis: Nach (R3) gibt es drei Punkte p1, p2 und p3, die nicht auf einer Geraden liegen. Dann sind (p1,p2), (p1,p3) und (p2,p3) drei Geraden, die sich nicht in einem Punkt treffen.
Lemma: Durch jeden Punkt p gehen mindestens 3 Geraden.
Beweis: Nämlich zu den soeben definierten drei Geraden die Parallelen durch p.
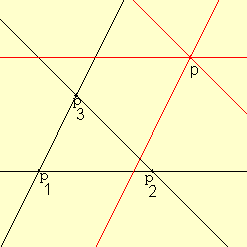
 Lemma: Auf jeder Geraden liegen mindestens 2 Punkte.
Lemma: Auf jeder Geraden liegen mindestens 2 Punkte.
Beweis: Sei g eine Gerade. Wähle einen beliebigen Punkt p der Ebene. Durch p verlaufen mindestens drei Geraden. Mindestens zwei davon sind nicht parallel zu g und schneiden also g in zwei verschiedenen Punkten.
Man kann zeigen:
Je zwei Geraden sind (als Punktmengen) gleichmächtig.
Je zwei Geradenbüschel sind gleichmächtig.
Bei endlichen affinenen Ebenen ist die Anzahl der Punkte eine Quadratzahl.
Kollineationen
Jede mathematische Struktur hat einen Isomorphibegriff und beschränkt sich bei der Untersuchung von Eigenschaften "bis auf Isomorphie". Ein Isomprphismus bei Räumen (Ebenen) erhält nach folgender Definition die Inzidenzstruktur.Definition: Eine Bijektion φ ist eine Kollineation, wenn gilt:
Die Punkte x, y, z sind genau dann kollinear, wenn auch die Bildpunkte φ(x), φ(y) und φ(z) kollinear sind.
Eine Kollineationen φ bildet also alle Geraden g auf alle Geraden φ(g) = {φ(x)|xεg} des Bildraumes ab.
Existiert eine Kollineation von einem linearen Raum (auch affine Ebene) in einen anderen, so nennt man die Räume (Ebenen) isomorrph.
Im Folgenden betrachten wir Kollineationen eines Raumes (einer Ebene) auf sich (In Diesem Fall nennt man die Isomorphie Automorphismus).
Satz: Die Kollineationen bilden eine Gruppe.
Beweis: Zu beweisen ist, dass die Verkettung zweier Kollineationen und die Umkehrabbildung einer Kollineation jeweils eine Kollineation ist. Beides ist offensichtlich.
Lemma: Bei einer Kollineation werden parallele Geraden auf parallele Geraden abgebildet.
Beweis: Haben die Bildgeraden einen Punkt gemeinsam, dann muss das Urbild dieses Punktes ein gemeinsamer Punkt der Geraden sein.
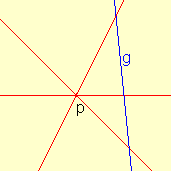
Definition: Eine Gerade a heißt Fixpunktgerade oder Achse einer Kollineation φ, wenn φ(p)=p für alle pεa ist.
Definition: Eine Punkt z heißt Zentrum einer Kollineation φ, wenn alle Geraden durch z auf sich selbst abgebildet werden. In einem affinen Raum nennt man solch eine Abbildung Streckung mit Zentrum z.
Das heißt: z ist Zentrum <=> Alle Geraden g mit zεg sind Fixgeraden (d.h. φ(g) = g).
Fixgerade (φ(g) =g) bedeutet dann, dass die Punkte von g bezüglich φ auf g "verschoben" werden.
Hier wird folgender Satz zur projektiven Ebene, die hier nicht behandelt wird, nur erwähnt:
Satz: Die affinen Kollineationen können zu projektiven Kollineationen fortgesetzt werden, wobei die "Ferngerade" Fixgerade ist. Projektive Kollineationen haben genau dann eine Achse, wenn sie ein Zentrum besitzen.
Das folgende bezieht sich wieder auf affine Kollineationen.
Satz: Eine Kollineation mit drei nicht kollienaren Fixpunkten ist die Identität.
Lemma: Alle Kollineationen mit der Achse a bilden eine Untergruppe.
Lemma: Alle Kollineationen mit dem Zentrum z bilden eine Untergruppe.
 Definition: Eine Kollineation heißt
Dilatation, wenn jede Gerade g auf eine zu g parallel Gerade abgebildet wird. (Die Identität gehört zu den Dilatationen).
Definition: Eine Kollineation heißt
Dilatation, wenn jede Gerade g auf eine zu g parallel Gerade abgebildet wird. (Die Identität gehört zu den Dilatationen).
(Bei der weiter oben erwähnten zugeordneten projektiven Kollineationen handelt es sich bei Dilatationen um Kollineationen, bei denen die "Ferngerade" Achse ist.)
Eine Dilatation hat höchstens einen Fixpunkt z. In diesem Fall heißt die Dilatation Zentralstreckung (mit Zentrum z).
Satz: Eine Streckung mit Zentrum z ist eine Zentralstreckung. D.h. Sind die Geraden durch z Fixgeraden, so wird jede Gerade g auf eine zu g parallel Gerade abgebildet.
Definition: Die Identische Abbildung und jede fixpunktfreie Dilatationen heißt Translation.
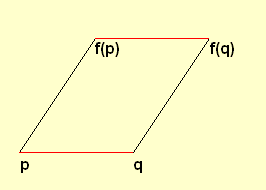 Es gilt:
Es gilt:
Satz: Eine von der Identität verschiedene fixpunktfreie Kollineation f ist genau dann eine Translation, wenn für alle Punkte p,q gilt: pf(p) ist parallel zu qf(q) ("Richtungstreue").
Satz: ("Eindeutigkeit der Translation") Zwei Translationen f und g sind gleich, wenn für einen Punkt p gilt: f(p) = g(p).
Satz: Die Dilatationen bilden eine Untergruppe und die Translationen einen Normalteiler der Kollineationsgruppe.
Translationsebenen
Definition: Eine affine Ebene heißt
Translationsebene, wenn gilt:
I) Für je zwei Punkte p und q existiert eine Translation mit f(p) = q. (Die Translationsgruppe heißt dann transitiv auf der Punktmenge.)
I) Für je zwei Punkte p und q existiert eine Translation mit f(p) = q. (Die Translationsgruppe heißt dann transitiv auf der Punktmenge.)
Im Folgenden sei die affine Ebene stets eine Translationsebe.
Die in I erwähnte Translation, die p auf q abbildet, ist eindeutig bestimmt. Die Translationsgruppe ist deshalb sogar scharf transitiv.
Man kann zeigen, dass die Translationsgruppe einer Translationsebene kommutativ ist.
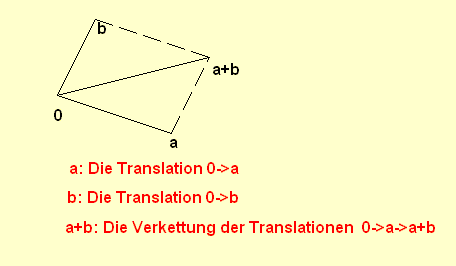 Wir wählen auf der affinen Ebene einen (willkürlichen) Punkt 0, genannt
Ursprung. Dann kann man jedem Punkt a genau eine Translation τa mit τa(0)=a zuordnen. Diese Zuordnung ist eine bijektive Abbildung von der Punktmenge auf die (kommutative) Translationsgruppe.
Wir wählen auf der affinen Ebene einen (willkürlichen) Punkt 0, genannt
Ursprung. Dann kann man jedem Punkt a genau eine Translation τa mit τa(0)=a zuordnen. Diese Zuordnung ist eine bijektive Abbildung von der Punktmenge auf die (kommutative) Translationsgruppe.
Im folgenden identifizieren wir die Punkte mit den Translationen. Die Punktemenge wird dadurch zu einer kommutativen Gruppe (G,+).
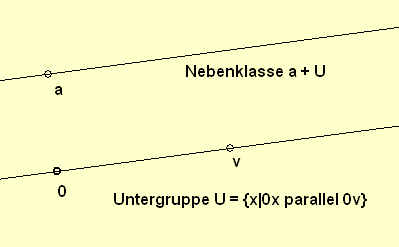 Die Ursprungsgeraden (die Geraden durch 0) sind dann genau die Untergruppen.
Die Ursprungsgeraden (die Geraden durch 0) sind dann genau die Untergruppen.
Und die Geraden parallel zu einer Ursprungsgeraden U sind genau die Nebenklassen zu der entsprechenden Untergruppen
a+U = {a+x|x ε U} (a ε G).
Die Ursprungsgeraden als Untergruppen der Translationsgruppe G betrachtet bilden eine "
Partition", d.h. es gilt:
(P1a) Jede Ursprungsgerade U ist verschieden von der Untergruppe {0} und es gibt mindestens zwei (verschiedene) Ursprungsgeraden.
(P1b) Für zwei verschiedene Ursprungsgeraden V1 und V2 gilt:
V1+V2 = {v1+v2|v1εV1,v2εV2} =G und V1∩V2={0}
(P2) Für alle Punkte vεG, v≠0, gibt es eine Ursprungsgerade V mit vεV,
Umgekehrt kann man aus einer Gruppe mit Partition, bei der also für eine Teilmenge der Untergruppen (P1)=(P1a)+(P1b), und (P2) gilt, entsprechend eine affine Translationsebene bilden, die isomorph zur Translationsgruppe ist (also auch kommutativ).
Bei Desargueschen Ebenen ist G ein Vektorraum. (P1) besagt dann, dass dieser die Dimension 2 hat.
(P1a) Jede Ursprungsgerade U ist verschieden von der Untergruppe {0} und es gibt mindestens zwei (verschiedene) Ursprungsgeraden.
(P1b) Für zwei verschiedene Ursprungsgeraden V1 und V2 gilt:
V1+V2 = {v1+v2|v1εV1,v2εV2} =G und V1∩V2={0}
(P2) Für alle Punkte vεG, v≠0, gibt es eine Ursprungsgerade V mit vεV,
Umgekehrt kann man aus einer Gruppe mit Partition, bei der also für eine Teilmenge der Untergruppen (P1)=(P1a)+(P1b), und (P2) gilt, entsprechend eine affine Translationsebene bilden, die isomorph zur Translationsgruppe ist (also auch kommutativ).
Bei Desargueschen Ebenen ist G ein Vektorraum. (P1) besagt dann, dass dieser die Dimension 2 hat.
Desarguesche affine Ebenen
Definition: Eine affine Ebene heißt
Desarguesche affine Ebene, wenn gilt:
I) Für je zwei Punkte p und q existiert eine Translation mit f(p) = q. (Die Translationsgruppe ist dann scharf transitiv auf der Punktmenge.)
II. Zu je drei kollinearen Punkten c, p, q existiert eine Zentralstreckung φ mit c als Fixpunkt undφ(p)=q
I) Für je zwei Punkte p und q existiert eine Translation mit f(p) = q. (Die Translationsgruppe ist dann scharf transitiv auf der Punktmenge.)
II. Zu je drei kollinearen Punkten c, p, q existiert eine Zentralstreckung φ mit c als Fixpunkt und
Im Folgenden sei die affine Ebene stets eine Desarguesche Ebene.
Man kann zeigen, dass die Eigenschaft II schon erfüllt ist, wenn es einen Punkt c gibt mit der Eigenschaft, dass für je zwei Punkte p und q (c, p und q kollinear) eine Zentralstreckung φ mit c als Fixpunkt und φ(p) =q existiert.
Die Translationen bilden einen kommutativen Normalteiler der Gruppe der Dilatationen und der Gruppe der Kollineationen.
Satz: Eine affine Ebene ist genau dann eine Desarguesche affine Ebenen, wenn in ihr der Satz von Desargues gilt.
Hauptsatz der Desarguesche affine Ebenen: Sei (G,+) die Translationgsruppe einer Desarguesche affine Ebene.
Dann existiert ein Schiefkörper K so, dass die Ebene isomorph zu der affinen Ebene (G,G1) ist, wobei G ein zweidimensionaler Vektorraum über K und die "Geraden" G1 von G die eindimensionalen affinen Unterräume {p+k·v|k ε K} von G für p, v ε G sind.
Dann existiert ein Schiefkörper K so, dass die Ebene isomorph zu der affinen Ebene (G,G1) ist, wobei G ein zweidimensionaler Vektorraum über K und die "Geraden" G1 von G die eindimensionalen affinen Unterräume {p+k·v|k ε K} von G für p, v ε G sind.
Die "Konstruktion" der Schiefkörpers K und des Vektorraumes G erfolgt folgendermaßen:
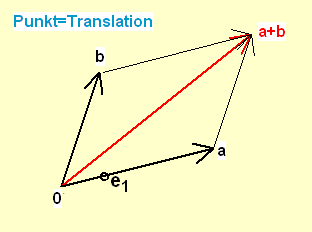
Wähle auf der affinen Ebene einen (willkürlichen) Punkt 0 Wir identifizieren Punkte a und b mit der Translation, die 0 auf a und 0 auf b abbildet und definieren die Addition "a+b" von a und b als die Verkettung dieser beiden Translationen. Damit ist die Punktemenge mit der Struktur der (kommutativen) Translationsgruppe (G,+) versehen.
Jede Dilatation φ mit Fixpunkt 0 (φ ist also eine Zentralstreckung) ist dann ein Automorphismus im Endomorphismenring von (G,+). Es gilt dann also für alle Punkte a und b die Regel:
φ(a+b) = φ(a) + φ(b).
Zum Beweis müssen wird die Translation a und b noch einmal als Abbildungen: τa und τb bezeichnen.
Es sei also τa die Translation mit τa(0) = a und τb die Translation mit τb(0) = b.
Die "Summe" a+b ist dann τa(b) dieser beiden Translationen.
Also gilt für eine Kollineation φ mit mit φ(0)=0:
φ(a+b) = φ(τa(b)) = φ(τaoτb(0)) =(φoτaoφ-1)o(φoτboφ-1)(0) =(φoτaoφ-1)(0) + (φoτboφ-1)(0)
=φoτa(0) + φoτb(0) = φ(a) + φ(b) ∎
Die Zentralstreckungen mit Fixpunkt 0 besitzen eine natürliche Multiplikation: die Verkettung.
Um K mit einer Körperstruktur auszustatten fehlt noch eine Addition. Diese wird folgendermaßen "punktweise" definiert:
Wähle einen zweiten (willkürlichen Punkt) e1 (0≠e1).
Zu jedem Punkt a (a≠0) auf der Geraden 0e1 gibt es genau eine Zentralstreckung φa mit Fixpunkt 0, die e1 auf a abbildet.
Die Addition zweier Elemente φa1 und φa2 von K wird definiert zu φa1+a2 (a1, a2 ε 0e1).
Man kann beweisen, dass mit dieser Addition und Multiplikation K ein Schiefkörper ist.
Das Nullelement des Schiefkörpers ist die Abbildung a→0 für alle aεG.
Das Einelement ist die Identität a→a für alle aεG.
Und die Punktebene ist ein zweidimensionaler Vektorraum über K ist, wobei die Skalarmultiplikation eines Vektors b mit einem "Skalar" φa die Translation φa(b) ist.
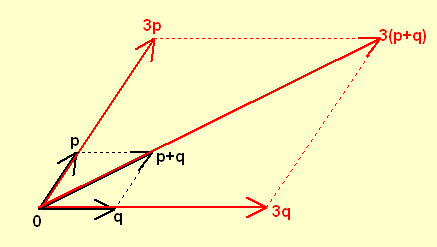 Beispiel:
Beispiel:
Sei 3p=p+p+p ≠ 0. Dann ist zum Beispiel die Abbildung p → p+p+p=3p eine Zentralstreckung mit Fixpunkt 0.
Präeuklidische Ebenen
Definition: Eine affinen Ebene heißt Präeuklidische Ebene, wenn noch eine Relation ≡ auf der Menge der Punktepaare, genannt Kongruenz, mit folgenden Eigenschaften existiert:- (a,b)≡(a,b) "Die Kongruenz ist als Äquivalenzrelation reflexiv"
- (a,b)≡(c,d) => (c,d)≡(a,b) "Die Kongruenz ist als Äquivalenzrelation symmetrisch"
- (a,b)≡(c,d) und (c,d)≡(e,f) => (a,b)≡(e,f) ("Die Kongruenz ist als Äquivalenzrelation transitiv")
- (a,b)≡(b,a) ("Symmetrie der Streckenkongruenz")
- (a,b)≡(x,x) => a=b ("Länge Null der Streckenkongruenz nur bei gleichen Punkten
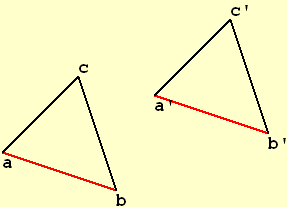 Für je zwei nicht-ausgeartete Dreiecke abc und a'b'c' mit (a,b) parallel (a',b'), (a,c) parallel (a',c') und (b,c) parallel (b',c') gilt:
Für je zwei nicht-ausgeartete Dreiecke abc und a'b'c' mit (a,b) parallel (a',b'), (a,c) parallel (a',c') und (b,c) parallel (b',c') gilt:
(a,b)≡(a',b') => (a,c)≡(a',c') und (b,c)≡(b',c')
("Parallele Dreiecke sind kongruent, wenn eine Seite kongruent zur entsprechenden Seite ist")
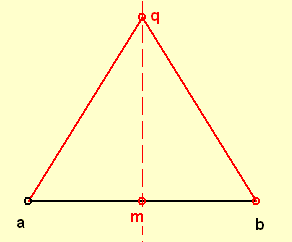 Zu je zwei Punkten a und b (a≠b) ist
Zu je zwei Punkten a und b (a≠b) ist
g={q|q ist Punkt und (a,q)≡(b,q)}
eine Gerade, die die Gerade ab (in der "Mitte" m) schneidet.
Die "Mittelinie" g nennt man dann orthogonal zu ab (siehe unten) und deshalb heißt sie Mittelsenkrechte.
("Jede Strecke hat eine Mittelsenkrechte")
Die Eigenschaften (i) bis (iii) machen die Relation "≡" zu einer Äquivalenzrelation,
die Eigenschaften (iv) und (v) zu einer Streckenkongruenz
und die Eigenschaften (vi) bis (vii) schließlich die affine Ebene zu einer präeuklidischen Ebene.
Im Folgenden sei die affine Ebene stets eine präeuklidische Ebene.
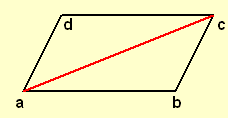 Satz: In einem nicht ausgeartetet Parallelogramm sind gegenüberliegende Seiten kongruent.
Satz: In einem nicht ausgeartetet Parallelogramm sind gegenüberliegende Seiten kongruent.
Voraussetzung: (a,b) parallel (c,d) und (a,d) parallel (b,c).
Behauptung: (a,b)≡(c,d) und (a,d)≡(b,c).
Beweis: Die Dreiecke abc und cda sind kongruent (siehe vi). Daraus folgt die Behauptung.
 Folgerung: Bei einer Translation f werden Strecken pq auf kongruente f(p)f(q) Strecken abgebildet.
Folgerung: Bei einer Translation f werden Strecken pq auf kongruente f(p)f(q) Strecken abgebildet.
Beweis: Mit pq parallel f(p)f(q) ist auch pf(p) parallel zu qf(q). Somit ist pqf(q)f(p) ein Parallelogramm und damit pq≡f(p)f(q).
Folgerungen:
Der Mittelpunkt m einer Strecke ab ist als Schnittpunkt der Geraden ab mit seiner Mittelsenkrechten eindeutig bestimmt.
Strecken lassen sich verdoppeln, d.h. zu zwei Punkten a,b (a≠b) existiert ein Punkt c (c≠a) auf der Geraden (a,b) so, dass (a,b) kongruent (b,c) ist. Der Punkt c heißt Verdopplungspunkt von a bezüglich b. (Man kann nämlich zeigen, dass dieser Punkt eindutig bestimmt ist.)
Die Diagonalen eines Parallelogramms schneiden sich im Mittelpunkt der beiden Diagonalen.
Umkehrung: Schneiden sich in einem Viereck die Diagonalen im Mittelpunkt, so ist das Viereck ein Parallelogramm.
Definition: Die Gerade g ist orthogonal zu der Geraden h, wenn es Punkte a und b auf g so gibt, dass h die Mittelsenkrechte der Strecke ab ist.
Man kann folgendes zeigen:
- g orthogonal zu h => h orthogonal zu g.
- g orthogonal zu h und h parallel zu h' => g orthogonal zu h'.
- Durch jeden Punkt einer Geraden verläuft eine orthogonale Gerade.
- Zu jedem Punkt und jeder Geraden gibt es eine orthogonale Gerade durch den Punkt.
Definition: Eine Kollineation, die die Kongruenz erhält, heißt Kongruenzabbildung oder Bewegung. (Die Kongruenz bei einer Abbildung f wird erhalten, wenn für Punkte a und b (f(a),f(b)) kongruent zu (a,b) ist.)
Satz: Jede Bijektion, die die Kongruenz erhält, ist eine Kollineation, also eine Kongruenzabbildung.
Satz: (i) Jede Punktspiegelung, das ist eine involutorische Zentralstreckung, ist eine Kongruenzabbildung.
(ii) Zu jedem Punkt z gibt es genau eine Punktspiegelung mit Zentrum z.
(iii) Die Punktspiegelung an der Mitte der Punkte a und b bildet a auf b ab.
(iv) Die Verkettung zweier Punktspiegelungen ist eine Translation.
Damit kann man beweisen, dass die Translationen (scharf) transitiv auf der Punktmenge sind.
Satz: (i) Jede Geradenspiegelung, das ist eine Abbildung die man mit Hilfe des eindeutig bestimmten Lotes und der Eindeutigkeit der Streckenverdopplung definiert, ist eine Kongruenzabbildung.
(ii) Bei der Geradenspiegelung an g ist g Achse (Fixpunktgerade).
(iii) Bei einer Geradenspiegelung an g ist das Mittellot von p und Bildpunkt von p für jeden Nichtfixpunkt p auf der Achse g.
(iv) Die Fixgeraden einer Geradenspiegelung an g sind (außer g noch) die Lote auf g.
(v) Eine Kongruenzabbildung mit zwei oder mehr Fixpunkten ist die Idendität oder eine Geradenspiegelung.
Satz: Eine involutorische Kongruenzabbildung ist eine Punkt- oder eine Geradenspiegelung.
Klassische Sätze kann man in der üblichen Weise beweisen.
- Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt, dem Umkreismittelpunkt.
- Die Höhen eines Dreiecks schneiden sich in einem Punkt.
- Satz des Thales: Für die Strecke ab und der Mitte m von ab gilt:
(Kreis um m durch a und ) =Def. {x Punkt | mx≡ma} = {x Punkt | x=a, x=b oder (x,a) senkrecht (x,b)} - Jede Kongruenzabbildung ist das Produkt von höchstens drei Geradenspiegelungen.
Folgerung: Zu je drei kollinearen Punkten c, p, q existiert eine Zentralstreckung φ mit c als Fixpunkt und φ(p)=q
Somit ist gezeigt:
Präeuklidischen Ebenen sind Desarguesche Ebenen.
Wir können eine präeuklidische Ebene also als Vektorraum G der Dimension 2 mit dem Nullvektor 0 betrachten über dem (Schief-)Körper K der Zentralstreckungen mit Fixpunkt 0 (Tatsächlich ist bei präeuklidischen Ebenen der (Schief-)Körper K dann kommutativ und seine Charakteristik ≠ 2).
Die Geraden sind dann die Punktemengen a+K·b (a, b ε G, b≠0).
Das gilt auch für desuargsche Ebenen. Darüber hinaus kann man bei präeuklidischen Ebenen den Vektorraum G als eine besondere Körpererweiterung des Körpers K der folgenden Art betrachten (wird später noch präzisiert.)
Satz: Sei G eine Körpererweiterung des Körpers K der Charakteristik ≠ 2 mit einem involutorischen Körperautomprphismus x→x- mit K={xεG|x=x-} als Fixkörper und sei iεG mit i≠0 und i- = -1.
Dann kann man leicht zeigen:
- (i) (1/i)- = 1/i- = -1/i
- (ii) i·K ={xεG|x-=-x}
- (iii) {1,i} bilden eine Basis von G als Vektorraum über K betrachtet. G hat also die Dimension 2.
- (iv) G ist Punktraum einer affinen Ebene, wobei die Geraden die Nebenklassen {a+b·K|a,bεG} sind.
Satz: Präeuklidische Ebene sind (bis auf Isomorphie) von folgender Form:
Es sei K ein (kommutativer) Körper der Charakteristik ≠ 2 und G eine Körpererweiterung von K mit einem involutorischen Körperautomorphismus x→x-, der verschieden ist von der Identität, wobei K = {xεG | x = x-} der Fixkörper ist. Dann lässt sich folgendermaßen eine präeuklidische Ebene konstruieren:
- Die Punkte sind die Elemente von G
- Die Geraden sind von der Form a+b·K (a,bεG)
- (a,b)≡(c,d) <=> (b-a)·(b-a)- = (d-c)·(d-c)-
Das klassische Beispiel ist natürlich die komplexe Zahlenebene mit dem involuorischen Körperautomorphismus
a + b·i → a - b·i (a,b ε R, i2 = -1.
Ein weniger triviales Beispiel ist:
 Beispiel: Sei K=Q der Körper der rationalen Zahlen und G=Q(√2) die Erweiterung von Q mit √2.
Beispiel: Sei K=Q der Körper der rationalen Zahlen und G=Q(√2) die Erweiterung von Q mit √2.
Dann läßt sich jedes Element von G eindeutig darstellen als a+b√2 (a,bεQ; in der Zeichnung a in horizontaler und b in vertikaler Richtung)
a + b√2 → a - b√2 ist ein involutorischer Automorphismus.
Die Mittelsenkrechte g der Strecke [-1,1] von -1 nach 1 ist die Gerade {x√2|xεQ}, denn für q=x√2 (xεQ), a=-1 und b=1 gilt
(a-q)·(a-q)- = (b-q)·(b-q)- <=> (-1-x√2)·(-1+x√2) = (1-x√2)·(1+x√2) für alle xεQ. Es ist also die vertikale Achse.
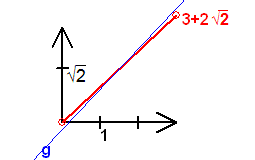
Berechnung der Mittelsenkrechte g der Strecke [0,3+2√2]:
Für einen Punkt q = x + y√2 der Mittelsenkrechten muss für a=0 und b=3+2√2 gelten:
(q-a)·(q-a)- = (q-b)·(q-b)- <=> (x+y√2)·(x-y√2) = (x+y√2-3-2√2)·(x-y√2-3+2√2).
Somit ist g={x+y√2|x,yεQ und y= 3/4*x-1/8} (In der Zeichnung blau).